Perfect Binary Tree

Complete binary trees are an important and general topic in the concept – of tree data structures. Before discussing a complete binary tree, we need to know the concept of tree data structures.

Tree data structures

A non–linear data structure that is hierarchical is known as the tree data structure. Numerous data structures are used in computer science to organize data into different formats. A tree typically consists of a root value and child nodes that branch out of its parent nodes to form subtrees. Non-linear data structures include trees.

There is no cap on how many child nodes a standard tree data structure can store. The binary tree and its various varieties are a particular tree data structure that will be covered in this article.

 A tree data structure is classified into six types:

1. Available trees.
2. Binary trees.
3. Binary search trees.
4. AVL tress (Adelson, Velsky and Em Landis tree).
5. Red – Black tree.
6. N – ary Tree.

What is Binary Tree Data Structure?

A binary tree is a non-linear data structure in the shape of a tree that can have up to two children for each parent. In addition to the data element, each node in a binary tree also carries a left and right reference. A tree's root node is node at the top of the hierarchy. The parent nodes are the nodes that house the sub-nodes.

The left and right children are the two child nodes of a parent node. Some applications that use a binary tree include hashing, data compression, routing data for network traffic, creating binary heaps, and binary search trees.

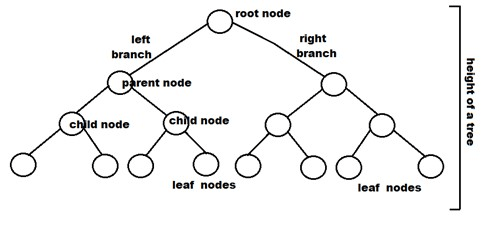
Terminologies associated with Binary Trees and Types of Binary Trees

1. Node: In a tree, it serves as the branching point.
2. Root: The topmost node of a tree.
3. Parent: A parent node is any node in a tree (other than the root) with at least one sub-node.
4. Child: When going away from the root, a child node is a node that immediately descends from a parent node.
5. External nodes include leaf nodes. They are the nodes without offspring.
6. Internal Node: These are inner nodes with at least one child, as the name implies.
7. Depth: The depth of a tree is the number of edges that extend from its node to its root.
8. Height: A tree's height is determined by counting the edges from the node to the deepest leaf.

Now that you know the terms used to describe binary trees and their many forms, it's time to comprehend the binary tree components.

Types of Binary Trees

There are different kinds of binary trees, and each kind has particular qualities. The specifics of each binary tree type are provided below:

1. Full binary trees.
2. Complete binary trees.
3. Perfect binary trees.
4. Balanced binary trees.
5. Degenerate binary trees.

Perfect binary tree

If every exterior or leaf node is at the same level or depth inside a tree and all internal nodes have exactly two offspring, a binary tree is said to be "perfect." A height "h" perfect binary tree has two h - 1 node. A perfect binary tree looks like this:

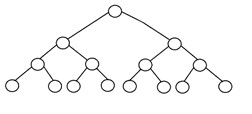
A sort of binary tree known as a perfect binary tree contains leaf nodes at the same level and inside nodes with exactly two children each.

Any internal node in a perfect binary tree has precisely two offspring, and all leaf nodes are located at the same level. This particular type of binary tree is known as a perfect binary tree.

The definition of a perfect binary tree is a binary tree in which each leaf node has the same level and either two offspring or none at all. The height or separation from the root node determines a node's level. A complete binary tree with a filled last level is called a perfect binary tree.

All internal nodes share a degree of 2.

If a single node has no children, it is a perfect binary tree with height h = 0. A node with h > 0 is a perfect binary tree if both subtrees are non-overlapping and have height h - 1.

Theorems of perfect binary tree

1. A complete binary tree with height h has nodes that are two h + 1 - 1.
2. The height of a perfect binary tree with n nodes is given by log(n + 1) - 1 = ln(n).
3. There are two h leaf nodes in a perfect binary tree of height h.
4. A node's average depth in a perfect binary tree is equal to ln(n).

Properties of perfect binary tree

1. Degree: The degree of a node in a tree is based on how many children it has. All internal nodes have a degree of 2. The leaf nodes of a perfect binary tree have a degree of 0.
2. Leaf node count: Since the last level is completely occupied, if the height of the perfect binary tree is h, the leaf node count will be two h.
3. Node depth: The average depth of a node in a perfect binary tree is (ln(n)).
4. Non-leaf nodes and leaf nodes are related. Non-leaf node count + one times the number of leaf nodes.
5. Total nodes: A tree of height h has a total node count of 2h+1 - 1 node. The tree's nodes are all filled. The nodes' sum is 20 + 21 +... + 2h = 2h+1 - 1.
6. Tree height: A perfect binary tree with N nodes has a height of log(N + 1) - 1 = ln(n). When computing the total number of nodes in a perfect binary tree, the relationship indicated can be used to compute this.

To check whether a given tree is a perfect binary tree or not:

1. Determine any node's depth (in the below tree, we find the depth of the leftmost node). Let d be the depth.
2. Recursively go through the tree now and look for the following two circumstances.
   1. Each internal node must have two non-empty children.
   1. Every leaf is at a depth.