Binary Tree to Single Linked List

In computer science, a binary tree is a type of data structure used to hold hierarchical data. It consists of left and right nodes, which can each have a maximal of two offspring. A binary tree may be navigated in a number of ways, such as in, pre-order, and post-order. The in-order traversal of such a binary tree and how to turn the binary tree into a single linked list will be the main topics of this essay.

The left subtree, the root node, and the right subtree are all visited during the in-order traversal of a binary tree. This traversal is frequently used to output a binary tree's nodes in sorted order. In this instance, however, the binary tree will be transformed into a linked list using the in-order traversal.

We must comprehend what kind of a linked list is before we can talk about the conversion procedure. A linked list is indeed a type of data structure made up of nodes that are connected by links. Each node inside the list does have a number and a reference to the following node. The list ends at the last node, which is indicated by a null pointer.

We shall employ a recursive method to transform a binary tree into a linked list. We'll go around the binary tree in sequence, adding a new node for every node we visit. The nodes inside a linked list will then be connected. This is the conversion process algorithm:

For each node inside the binary tree that is visited, a new node is created.

If there was a previously established node, connect it to the new node.

Change the freshly generated node's reference to null.

Return the connected list's head.

To further understand this approach, let's look at an illustration. Think about the subsequent binary tree:

This is how to transform this binary tree into a linked list step-by-step:

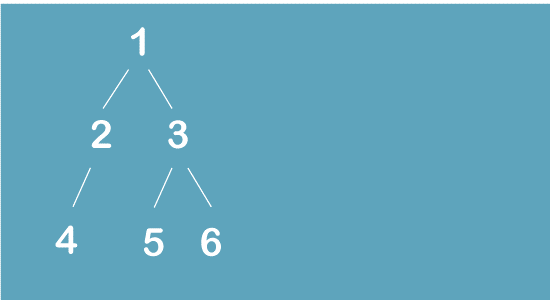
Step 1: Explore the root node's left subtree.

The root node, 1, serves as the starting point for the traverse. That left child node, number 2, is where we next go.

Step2: Set up a new node again for visited node in step two.

For node 2, we make a new node and set the value to 2.

Step 3: Connect the newly generated node to the original node.

As it is the first entry in the linked list, we reset its reference to null.

Step 4: Explore the visited node's left subtree.

We shift to node 4, which is node 2's leftmost sibling node.

Step5: Build a new node again for visited node in step five.

Step6: We add a new node and set the value to 4 for node 4.

Connect the new node towards the node that was already established in step six.

We connect it to the first node, node 2, since it is the second node inside the linked list.

Step 7: Make the newly generated node's pointer null.

We set its reference to null because it is the final node inside the linked list.

Step 8: Explore the visited node's right subtree.

Step9: Returning to node 2, we travel through node 5's right subtree.

Step10: Build a new node again for visited node in step nine.

For node 5, we make a new node and assign its number to 5.

Connect the new node towards the node that was previously established in step 10.

We connect it to the made previously node, which really is node 4, because it is the third node inside the linked list.

The following function is called to initiate the conversion process:

Node* convert(Node* root, Node* prev) {
    if (!root) return prev;
    prev = convert(root->left, prev);
    Node* new_node = new Node(root->data);
    if (!prev) {
        prev = new_node;
    } else {
        prev->next = new_node;
        prev = new_node;
    }
    prev = convert(root->right, prev);
    return prev;
}

The binary tree's root and a reference to the linked list's preceding node are the two inputs given to the convert function. A pointer towards the final node inside the linked list is returned by the function.

The root and the preceding node are both NULL in the initial call towards the convert function. The left subtree on node 1, which again is node 2, is the first path we take. Using the preceding node pointer and node 2, which is node 1's left child, we recursively run the convert function. The initial iterative call returns NULL since node 2 has had no left children.

The next step is to build a new node of node 2 and link it with the NULL prior node. The preceding node pointer is changed to point at node 2, which is the new node. The next step is to navigate node 4, the right subtree of node 2.

We create an entirely new node with node 4 and link this to node 2 because node 4 seems to have no children. The preceding node pointer is changed to point at node 4, which is the new node. After that, we provide the reference to node 4.