Minimum Spanning Tree
Before getting to know about the minimum spanning tree, we should first discuss about what is a spanning tree. A spanning tree is basically a sub or minimized graph that comes from an undirected graph. This means that a specific minimum spanning tree generally contains all the numbers of edges present in the graph and that too with almost the least type of edges. In case there appears to be a case where the vertex is skipped, then it is not considered as a spanning tree. The edges present in the spanning tree don’t contain the mass that is specified to them. Suppose we have a graph that contains the total ‘n’ number of edges, then the total amount of spanning trees that can be created is given by the expression; nn-2.
What is a minimum spanning tree?
The minimum spanning tree is often described as the one where the sum of the edges is the least or minimum. It is called a minimum spanning tree because in this, the cost is very little, or you can say the least when you compare it with the rest of the spanning trees. It is the kind of tree that has a great impact on the designing field and also in the networking areas. It is a tree that doesn’t contain any cycles within it and with the least possible weight. It is the one tree in which the combined weight or mass of all the edges turns out to be as small as possible.
Properties of the minimum spanning tree
There are mainly seven properties in a minimum spanning tree. We will discuss them one by one in detail below: -
- Multiplicity
Suppose if we have n number of edges present, then the minimum spanning tree is told to be n-1 edges. - Cut property
The cut property in an MST generally signifies that if we cut a graph of any sort, then the edge we just trimmed with the least weight will always be part of the minimum spanning tree. - Cycle property
The cycle property in an MST generally signifies that the edge which contains or occupies the maximum amount of weight will never be considered as a part of the minimum spanning tree. - Contraction
Let us suppose we have a tree which is called T and being a tree. It already has some edges within itself; then, we can simply converge this T into one single vertex while maintaining the relationship between the contracted graph and the graph before the contraction. - Uniqueness
If somehow, there is an edge that contains a distinct weight, then it will have one and only one minimum spanning tree. There are many applications rationalized based on the same principle; some of them are forests, telecommunication companies, and several others. - Least cost subgraph
If the measures we have, are somehow positive, then the minimum spanning tree actually turns into a minimum cost subgraph that helps us in linking all the edges and vertices. - Least cost edge
If we know that the minimum cost edge of a tree is somewhat unique, then the edges present in there are typically in any kind of MST, which is a minimum spanning tree.
Types of algorithms used
There are two major kinds of the algorithm used for finding out the minimum spanning tree. They are: -
- Kruskal's algorithm
- Prim’s algorithm
Let us discuss them one by one.
Kruskal's algorithm
Kruskal’s algorithm is known for its application in finding the minimal spanning forest. In this algorithm, if the graph is combined, then it relocates the minimum spanning tree. It is known as a greedy algorithm in the history of graphs, as when we move ahead, we search for the next least weighted edge, which will not be able to form a wheel or cycle in the graph. It was discovered by Joseph Kruskal in the year 1956.
It is an algorithm that is particularly used for searching the minimum spanning tree for a graph that is interconnected and weighted in nature. The primary focus of the algorithm is to search and relocate the sub-group of edges by the usage of crossing each and every vertex of the whole graph. It escorts the approach that searches for an optimum resolution at each and every corner or stage rather than concentrating on a single global optimum.
Implementation of Kruskal's algorithm in C++
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
#define edge pair<int, int>
class Graph {
private:
vector<pair<int, edge> > G; // graph
vector<pair<int, edge> > T; // mst
int *parent;
int V; // number of vertices/nodes in graph
public:
Graph(int V);
void AddWeightedEdge(int u, int v, int w);
int find_set(int i);
void union_set(int u, int v);
void kruskal();
void print();
};
Graph::Graph(int V) {
parent = new int[V];
//i 0 1 2 3 4 5
//parent[i] 0 1 2 3 4 5
for (int i = 0; i < V; i++)
parent[i] = i;
G.clear();
T.clear();
}
void Graph::AddWeightedEdge(int u, int v, int w) {
G.push_back(make_pair(w, edge(u, v)));
}
int Graph::find_set(int i) {
// If i is the parent of itself
if (i == parent[i])
return i;
else
// Else if i is not the parent of itself
// Then, i is not the representative of his set,
// so we recursively call Find on its parent
return find_set(parent[i]);
}
void Graph::union_set(int u, int v) {
parent[u] = parent[v];
}
void Graph::kruskal() {
int i, uRep, vRep;
sort(G.begin(), G.end()); // increasing weight
for (i = 0; i < G.size(); i++) {
uRep = find_set(G[i].second.first);
vRep = find_set(G[i].second.second);
if (uRep != vRep) {
T.push_back(G[i]); // add to tree
union_set(uRep, vRep);
}
}
}
void Graph::print() {
cout << "Edge :"
<< " Weight" << endl;
for (int i = 0; i < T.size(); i++) {
cout << T[i].second.first << " - " << T[i].second.second << " : "
<< T[i].first;
cout << endl;
}
}
int main() {
Graph g(6);
g.AddWeightedEdge(0, 1, 4);
g.AddWeightedEdge(0, 2, 4);
g.AddWeightedEdge(1, 2, 2);
g.AddWeightedEdge(1, 0, 4);
g.AddWeightedEdge(2, 0, 4);
g.AddWeightedEdge(2, 1, 2);
g.AddWeightedEdge(2, 3, 3);
g.AddWeightedEdge(2, 5, 2);
g.AddWeightedEdge(2, 4, 4);
g.AddWeightedEdge(3, 2, 3);
g.AddWeightedEdge(3, 4, 3);
g.AddWeightedEdge(4, 2, 4);
g.AddWeightedEdge(4, 3, 3);
g.AddWeightedEdge(5, 2, 2);
g.AddWeightedEdge(5, 4, 3);
g.kruskal();
g.print();
return 0;
}
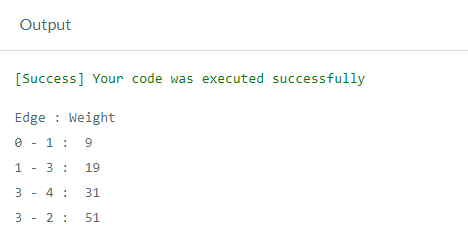
Output:
Prim’s Algorithm
Prim’s algorithm is used to find out the minimum spanning tree with a weighted undirected graph. What it means is that it purposely searches a sub-group of all the vertices or the edges of the tree, and after that, the total mass of the edges is reduced. This type of algorithm initially functions on the principle of constructing one vertex at a given point of time. From adding on and starting with any random vertex and then carrying out and connecting the cheapest possible connection from the tree to another vertex. Prim’s algorithm is known to be the one that begins with a specific vertex and then resumes in adding the edges with the tinniest weight unless and until the goal is reached.
Implementation of prim’s algorithm
#include <cstring>
#include <iostream>
using namespace std;
// the total amount of vertices in the graph is: -
#defining V 5
// Below, we will be creating a 2d array that has a size of 5*5
//We will now describe the adjacency matrix to simply present a graph
int G[X][X] = {
{0, 9, 75, 0, 0},
{9, 0, 95, 19, 42},
{75, 95, 0, 51, 66},
{0, 19, 51, 0, 31},
{0, 42, 66, 31, 0}};
int main() {
int n_edge; // total number of edges
// Now, we will create an array that will help us track all the chosen vertices
// the ones that are chosen will become true, and others will become false
int select[V];
// set the chosen false initially
memset(select, false, sizeof(selected));
// Now, we have to initialize and set the number of edges to 0
n_edge = 0;
// Depicting the number of edges in an MST: -
// It will always be less than (X-1), where we know that X is the number of vertices present
//graph is depicted below
// we will now select the 0th vertex and make it true
select[0] = true;
int a; // row number
int b; // col number
// present by printing the edge and weight
cout << "Edge"
<< " : "
<< "Weight";
cout << endl;
while (no_edge < X - 1) {
//For every single vertex in the set M, find all adjacent vertices
//count the distance from the vertex that was chosen in step 1.
// if by any chance the vertex is already present in set M then it’s fine. In any other case, dismiss it.
//Select any other vertex which is closest to the chosen vertex in step 1.
int min = INF;
a = 0;
b = 0;
for (int i = 0; i < X; i++) {
if (selected[i]) {
for (int j = 0; j < X; j++) {
if (!selected[j] && H[i][j]) { // not in selected and there is an edge
if (min > H[i][j]) {
min = H[i][j];
a = i;
b = j;
}
}
}
}
}
cout << a << " - " << b << " : " << H[a][b];
cout << endl;
selected[b] = true;
n_edge++;
}
return 0;
}
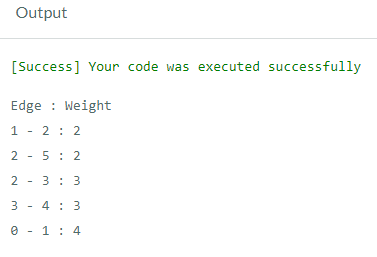
Output: