Digital Search Tree in Data Structures

What is a digital search Tree in Data Structures?

The Digital search tree is known for its application and diversity in the way it has impacted our world in the field of data structures. A Digital search tree is a binary tree that helps us access and manages all the data safely. The tree tends to hold only binary data and helps us. There seem to be a catch implying that if the search tree started with a zero (0), then it is present in the left subtree of the search tree, and if the tree started with a one (1), then it is present in the right subtree of the search tree. Both sides of the tree worked exclusively to make the work of the tree efficient. It turned out to be one of the most useful discoveries in the field of data structures.

In this article section, we will observe the simple structure or model of the digital search tree that contains only 4 bits. Here is the picture: -

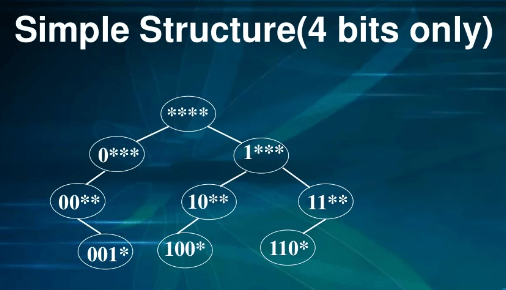
What distinguishes a DST from other trees?

When we talk about a basic binary tree, we realize that to move down the structure of the tree, we probably have to take into consideration the comparison that we do between the current node and the key that is being sorted at that particular time, but this is not the case with the Digital search tree, in these kinds of trees we just have to make usage of the bits of the keys which are being organized or sorted at the moment. For this to happen, this approach has a lot of determination plus commendable properties that we might use in the future.

The approach and algorithms that we use for positioning the node and the search drives are pretty basic and intuitive. When applying the search and insert methods, we generally have to use the basic DSTs techniques, and it doesn't require much modification when performing these functions. Furthermore, this approach doesn't tend to keep the additional data preserved in the nodes to maintain the order and balance of the tree. This technically helps eliminate the tree's extra spaces while doing the other approaches. The balancing element of the tree is pretty much managed by the depth of the tree, which is figured by the length of the tree. The length of the tree is generally counted by the number of bits present in that particular key.

Complexities

If the data is randomly distributed in the digital search tree, then the time taken to perform any operation in that tree will be calculated by O(log N), where N stands for the height of the digital search tree.

However, if the data is not sorted, which is the usual case in these types of trees, then the time taken to perform any operation will ultimately depend upon the number of bits present in the tree. So, the worst case will be calculated by O(b), where b stands for the number of bits.

Advantages of the digital search tree

• The main benefit of the digital search tree is that it occupies and consumes less space and memory as compared to the rest of the other trees, says AVL tree or binary tree.
• We don't have to compile any extra data or information to maintain the hierarchy of the tree because the depth of the tree is usually maintained by the length of the key. This key maintains the posture by keeping a count on the number of bits present.
• Multiple operations can take place very efficiently.
• Various operations such as deletion, insertion, or search can take place in DST much more easily as compared to the other trees such as binary search, AVL, or simply binary tree.

Disadvantages of the digital search tree

• If we are given a key or node with long data, and the comparison takes a lot of time, this can lead to a costly procedure.
• We already know that the operations we perform in these trees are conducted via bits, which can result in difficulties when handling bitwise.
• The data or records that we encounter are generally not organized.
• There might be a case where we encounter keys that have similar errors, and they have different lengths.