Heap Data Structure
In this article, we will learn in detail about Heap (Min heap and Max heap). Before going to the main topics, let’s have a look at what is complete binary tree?
What is a complete binary tree?
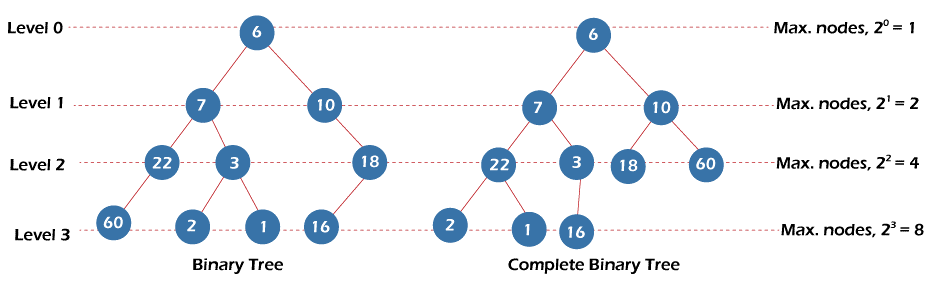
Complete binary tree - A binary tree is said to be a complete binary tree when all the levels except the last level must have the maximum number of nodes, and all the nodes at the last level should appear on the leftmost side as possible. For any node k, the left and right children can be found easily and are 2*k, and 2*k+1 and its parent would be lower bound (k/2).
To obtain a complete binary tree from a binary tree, we select all the nodes of the binary tree and start constructing a complete binary tree. Starting from the root node, we fill the nodes level-by-level. After filling a level to its maximum node capacity, we move to the next level and start adding the nodes from the leftmost side of the tree. And we can observe the difference between a binary tree and a complete tree in the figure given below:
Heap – In the data structure, a heap is a special type of complete binary tree categorized into Min Heap and Max Heap.
- Min heap – A complete binary tree is said to be a Min heap when the value of all the parent nodes is less than the value of their respective children or the value of all the children is greater than the value of their respective parent.
- Max Heap – A complete binary tree is said to be a Max heap when all the value of parent nodes is greater than the value of their respective children or all the value of children nodes is less than the value of their respective parent.
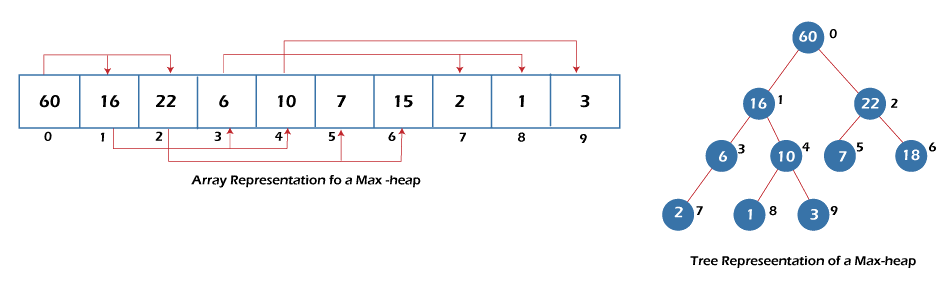
Representation of a heap – A max-heap or min-heap is represented in two forms:
- The array representation of a heap
- The tree representation of a heap
Now, let us look at how a max heap or Min heap is implemented.
- Max-heap implementation – A heap is implemented on an array, and the code of the same is given below:
C++ program to implement max-heap using an array is given below:
#include <iostream>
using namespace std;
int heap_size = 0; // Variable to store the current size of the heap
int heap_max_size; // Variable to store the max size of the heap
int key_value; // Variable to store the key value needs to be inserted in the heap
// Function to find the parent index of a node.
int parent_node(int k)
{
return (k - 1) / 2;
}
// Function to find the left child of a node.
int left_child(int k)
{
return 2 * k + 1;
}
// Function to find the right child of a node.
int right_child(int k)
{
return 2 * k + 2;
}
// Function to convert a tree of size n into a max heap.
void max_heapify(int arr[], int parent_index)
{
int left_child_index = left_child(parent_index); // Storing the index of the left child of a node.
int right_child_index = right_child(parent_index); // Storing the index of the right child of a node.
int largest_value_index = parent_index; // Largest_value_index stores the index of the largest of parent, right child, and left child.
// If the left child is in the heap and greater than the parent.
if (left_child_index < heap_size && arr[left_child_index] > arr[largest_value_index])
{
largest_value_index = left_child_index;
}
// If the right child is in the heap and greater than the parent.
if (right_child_index < heap_size && arr[right_child_index] > arr[largest_value_index])
{
largest_value_index = right_child_index;
}
// If the largest is not equal to parent.
if (largest_value_index != parent_index)
{
// Swapping the value largest value with its parent.
swap(arr[largest_value_index], arr[parent_index]);
// Calling the max_heapify function at index where the largest value was.
max_heapify(arr, largest_value_index);
}
}
// Function to place the newly added element at its correct position in a heap.
void build_max_heap(int arr[], int child_index)
{
// If the new added element was not added to the root node.
if (child_index != 0)
{
// Finding the parent of the newly added element.
int parent_index = parent_node(child_index);
// If the newly added element is greater than its parent.
if (arr[child_index] > arr[parent_index])
{
// Swapping the newly added element with its parent
swap(arr[child_index], arr[parent_index]);
// calling the build_max_heap function at the parent index.
build_max_heap(arr, parent_index);
}
}
}
// Function to insert an element in a heap
void insert(int arr[], int key_value)
{
// Increasing the size of the heap by 1.
heap_size += 1;
// Adding element at the last position in the heap.
arr[heap_size - 1] = key_value;
// Calling the build_max_heap at the last index.
build_max_heap(arr, heap_size - 1);
}
// Function to delete root node of the max heap.
void delete_root_node(int arr[])
{
// Storing the value of the last node.
int last_element = arr[heap_size - 1];
// Replacing the value of root node with the value of the last node.
arr[0] = last_element;
// Decreasing the size of the heap by 1.
heap_size -= 1;
// Heapifying the heap of size n-1.
max_heapify(arr, 0);
}
// Function to traverse all the elements of the heap.
void heap_traversal(int arr[])
{
// If heap has no nodes.
if (heap_size == 0)
{
cout << "No elements in the heap!" << endl;
return;
}
// Printing all the elements of the heap
cout << "Elements of the heap are: ";
for (int i = 0; i < heap_size; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
// Function to search in a heap using linear search
int search_in_heap(int arr[], int key_value)
{
// If heap size is not equal to zero.
if (heap_size != 0)
{
// Traversing all the elements of the heap.
for (int i = 0; i < heap_size; i++)
{
if (key_value == arr[i])
{
// If element is found.
return i;
}
}
}
// If element is not found.
return -1;
}
// Driver function
int main()
{
cout << "Enter the maximum size of the heap: ";
// Asking for the maximum size of the heap
cin >> heap_max_size;
// Creating an array of size entered by the user and initializing by 0.
// This method is called the dynamic memory allocation to an array.
int *arr = new int[heap_max_size]{0};
// Providing options to an user to perform its desire action.
cout << "Enter 1 to insert an element in a heap: " << endl;
cout << "Enter 2 to delete an element from the heap: " << endl;
cout << "Enter 3 to search an element in the heap: " << endl;
cout << "Enter 4 to print all the elements of the heap: " << endl;
cout << "Enter 5 to exit from the program: " << endl;
int choice, key_value, element_found;
do
{
// Asking for the choice
cout << "Enter your choice: ";
cin >> choice;
switch (choice)
{
// If choice is to insert an element
case 1:
cout << "Enter the value to insert in a heap: ";
cin >> key_value;
insert(arr, key_value);
break;
// If choice is to delete an element
case 2:
delete_root_node(arr);
break;
// If choice is to search an element
case 3:
cout << "Enter the value to search in the heap: ";
cin >> key_value;
element_found = search_in_heap(arr, key_value);
element_found > -1 ? cout << "Element is found at index = " << element_found << endl : cout << "The element is not present in the heap!" << endl;
break;
// If choice is to traverse all elements.
case 4:
heap_traversal(arr);
break;
// If the user wants to exit from the program
case 5:
cout << "Exited Successfully!";
break;
// In case of wrong inputs
default:
cout << "Wrong choice!" << endl;
break;
}
} while (choice != 5); // Condition to exit from the program
return 0;
}
The possible output of the above program:
Enter the maximum size of the heap: 20
// Output of inserting elements in a heap
Enter 1 to insert an element in a heap:
Enter 2 to delete an element from the heap:
Enter 3 to search an element in the heap:
Enter 4 to print all the elements of the heap:
Enter 5 to exit from the program:
Enter your choice: 1
Enter the value to insert in a heap: 6
Enter your choice: 1
Enter the value to insert in a heap: 7
Enter your choice: 1
Enter the value to insert in a heap: 10
Enter your choice: 1
Enter the value to insert in a heap: 22
Enter your choice: 1
Enter the value to insert in a heap: 3
Enter your choice: 1
Enter the value to insert in a heap: 18
Enter your choice: 1
Enter the value to insert in a heap: 60
Enter your choice: 1
Enter the value to insert in a heap: 2
Enter your choice: 1
Enter the value to insert in a heap: 1
Enter your choice: 1
Enter the value to insert in a heap: 16
Enter your choice: 4
// Output of traversing a heap
Elements of the heap are: 60 16 22 6 10 7 18 2 1 3
// Output of searching in a heap
Enter your choice: 3
Enter the value to search in a heap: 10
Element is found at index = 4
Enter your choice: 3
Enter the value to search in a heap: 16
Element is found at index = 1
Enter your choice: 3
Enter the value to search in a heap: 23
The element is not present in the heap!
// Output of deleting the root node in a heap
Enter your choice: 4
Elements of the heap are: 60 16 22 6 10 7 18 2 1 3
Enter your choice: 2
Enter your choice: 4
Elements of the heap are: 22 16 18 6 10 7 3 2 1
Enter your choice: 5
Exited Successfully!
Let us understand the above program and its functions step by step:
One might get confused about how the heap is implemented using an array. But it is very simple to understand.
- Insertion in a heap: Here, we are constructing a heap starting from size zero. The code of the insertion is explained below:
void build_max_heap(int arr[], int child_index)
{
if (child_index != 0)
{
int parent_index = parent_node(child_index);
if (arr[child_index] > arr[parent_index])
{
swap(arr[child_index], arr[parent_index]);
build_max_heap(arr, parent_index);
}
}
}
void insert(int arr[], int key_value)
{
heap_size += 1;
arr[heap_size - 1] = key_value;
build_max_heap(arr, heap_size - 1);
}
Now, the first element inserted in the Max heap is 6. The insert function will call the build max heap function to place 6 at its correct position in the Max heap, but we know a heap with one node is min, and max heap means 6 is added at its correct position as of now. The heap size is now 1.
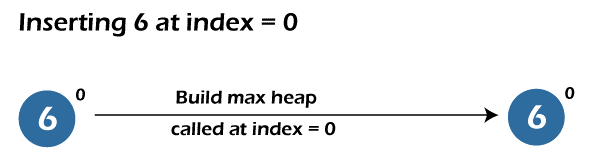
The second element inserted in the max heap is 7. We will add 7 at the end of the max heap and call the build max heap function to place 7 at its correct position in the Max heap. The build max heap will compare it with its parent, which is 6. Here, 7 is greater than 6, both are swapped, and the build max heap function will be called at the parent index to check further whether 7 is at its correct position or not. As of now, 7 is at its correct position.
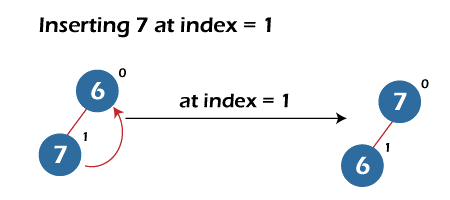
The third element inserted is 10. It is added at the end of the heap, and the build max function is called to place 10 at its correct position. The build max heap function compares it with its parent, which is 6 here and less than 10. Now both are swapped, and the build max heap is again called at the parent index to check whether the 10 is placed at its correct position in the max heap or not.
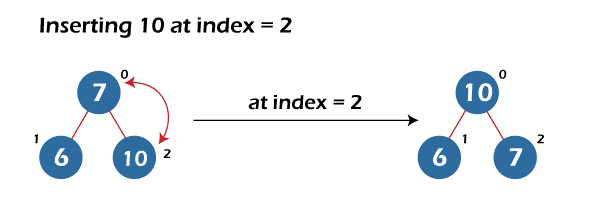
The fourth element inserted is 22. It is added at the end of the max heap. The build max heap function is called to place 22 at its correct position. It will compare it with its parent, which is 7 here and less than 22. Now, both are swapped, and the build max heap function is called at the parent index to check whether 22 is placed at its correct position or not. Here, the parent of 22 is 10, which is less than 22. Now, both are swapped, and the build max heap function is again called at the parent index.
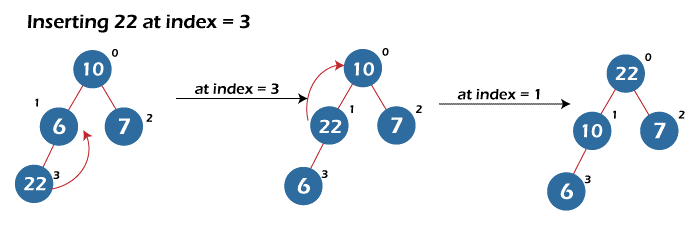
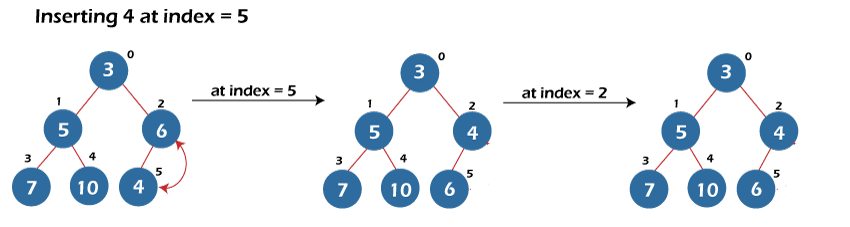
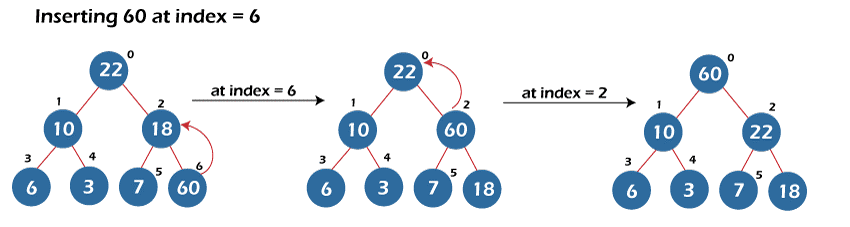
The other insertion of the elements is shown below in the tree representation:

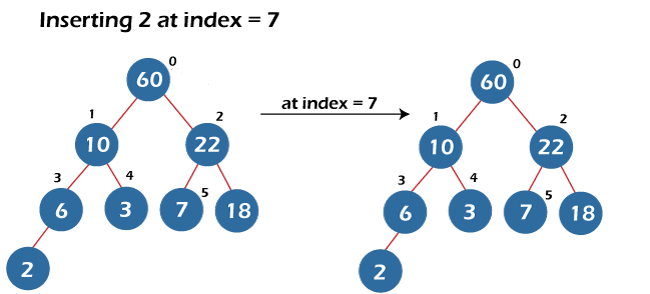
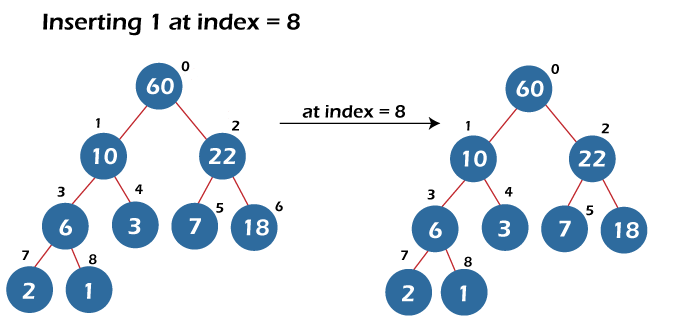
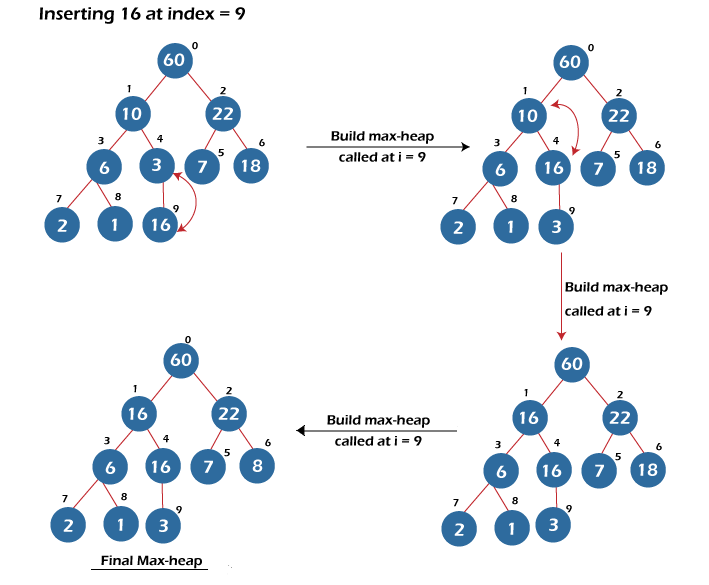
- Deletion in a heap – The standard delete operation performed on a heap is to delete the root element, i.e., the largest element if the heap is a max-heap or the smallest element if it is a min-heap. Deleting the random elements in a heap is time costly because we first need to perform a search operation to find that particular element in a heap.
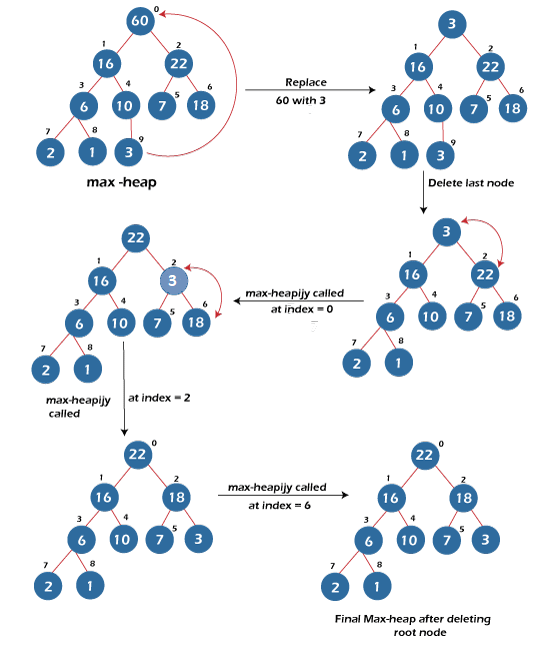
Steps involved in the deletion of a node in a heap:
- We swap the root node with the last node (or the last element). To delete a random element, we first find its index and then swap it with the last element.
- Delete the last node by decreasing the size of the heap by 1.
- Now, we call the max-heapify function to place the root value at its correct position.
The code of the delete function and max-heapify function is given below:
void max_heapify(int arr[], int parent_index)
{
int left_child_index = left_child(parent_index);
int right_child_index = right_child(parent_index);
int largest_value_index = parent_index;
if (left_child_index < heap_size && arr[left_child_index] > arr[largest_value_index])
{
largest_value_index = left_child_index;
}
if (right_child_index < heap_size && arr[right_child_index] > arr[largest_value_index])
{
largest_value_index = right_child_index;
}
if (largest_value_index != parent_index)
{
swap(arr[largest_value_index], arr[parent_index]);
max_heapify(arr, largest_value_index);
}
}
void delete_root_node(int arr[])
{
int last_element = arr[heap_size - 1];
arr[0] = last_element;
heap_size -= 1;
max_heapify(arr, 0);
}
The deletion of the root node is shown in the figure given below:
- Searching in a Heap – A heap is not optimised to search a random element; instead, it is optimised to search minimum or maximum elements. This makes searching for random elements a non-standard operation of a heap. The time complexity of finding the minimum element in min-heap or maximum element in max-heap is O(1). To search a random element, we need to visit all the nodes, which makes its time complexity equal to O(n), the same as the time complexity of the linear search in an array.
We know that the heap is implemented using an array, so for searching a random element, we implement a linear search on it. And compares it with all the values stored starting from the root index.
The code of searching in a heap, i.e., linear search in a heap, is given below:
int search_in_heap(int arr[], int key_value)
{
if (heap_size != 0)
{
for (int i = 0; i < heap_size; i++)
{
if (key_value == arr[i])
{
return i;
}
}
}
return -1;
}
The above code returns the key-value index if it is found and -1 if the element is not found.
Searching for a random element is also shown in the figure given below:
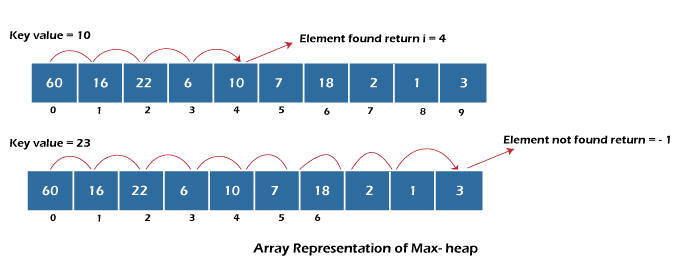
- Heap Traversal – The traversal of all the nodes in a heap is done linearly. We visit nodes starting from the root node to the last node and print all the values.
The code of heap traversal is given below:
void heap_traversal(int arr[])
{
if (heap_size == 0)
{
cout << "No elements in the heap!" << endl;
return;
}
cout << "Elements of the heap are: ";
for (int i = 0; i < heap_size; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
We have done the traversal using a for loop starting from 0 indexes to the heap size and printing all the values as an output.
- Min-heap implementation – A min-heap is also implemented on an array, and the code of the same is given below:
C++ Program to implement min-heap using an array: The implementation of min-heap is similar to the max-heap implementation.
#include <iostream>
using namespace std;
int heap_size = 0; // Variable to store the current size of the heap
int heap_max_size; // Variable to store the max size of the heap
int key_value; // Variable to store the key value needs to be inserted in the heap
// Function to find the parent index of a node.
int parent_node(int k)
{
return (k - 1) / 2;
}
// Function to find the left child of a node.
int left_child(int k)
{
return 2 * k + 1;
}
// Function to find the right child of a node.
int right_child(int k)
{
return 2 * k + 2;
}
// Function to convert a tree of size n into a min heap.
void min_heapify(int arr[], int parent_index)
{
int left_child_index = left_child(parent_index); // Storing the index of the left child of a node.
int right_child_index = right_child(parent_index); // Storing the index of the right child of a node.
int smallest_value_index = parent_index; // Smallest_value_index stores the index of the smallest of parent, right child, and left child.
// If the left child is in the heap and smaller than the parent.
if (left_child_index < heap_size && arr[left_child_index] < arr[smallest_value_index])
{
smallest_value_index = left_child_index;
}
// If the right child is in the heap and smaller than the parent or its sibling.
if (right_child_index < heap_size && arr[right_child_index] < arr[smallest_value_index])
{
smallest_value_index = right_child_index;
}
// If the smallest is not equal to parent.
if (smallest_value_index != parent_index)
{
// Swapping the smallest value with its parent.
swap(arr[smallest_value_index], arr[parent_index]);
// Calling the min_heapify function at index where the smallest value was.
min_heapify(arr, smallest_value_index);
}
}
// Function to place the newly added element at its correct position in a heap.
void build_min_heap(int arr[], int child_index)
{
// If the new added element was not added to the root node.
if (child_index != 0)
{
// Finding the parent of the newly added element.
int parent_index = parent_node(child_index);
// If the newly added element is smaller than its parent.
if (arr[child_index] < arr[parent_index])
{
// Swapping the newly added element with its parent
swap(arr[child_index], arr[parent_index]);
// calling the build_min_heap function at the parent index.
build_min_heap(arr, parent_index);
}
}
}
// Function to insert an element in a heap
void insert(int arr[], int key_value)
{
// Increasing the size of the heap by 1.
heap_size += 1;
// Adding element at the last position in the heap.
arr[heap_size - 1] = key_value;
// Calling the build_min_heap at the last index.
build_min_heap(arr, heap_size - 1);
}
// Function to delete root node of the min heap.
void delete_root_node(int arr[])
{
// Storing the value of the last node.
int last_element = arr[heap_size - 1];
// Replacing the value of root node with the value of the last node.
arr[0] = last_element;
// Decreasing the size of the heap by 1.
heap_size -= 1;
// Heapifying the heap of size n-1.
min_heapify(arr, 0);
}
// Function to traverse all the elements of the heap.
void heap_traversal(int arr[])
{
// If heap has no nodes.
if (heap_size == 0)
{
cout << "No elements in the heap!" << endl;
return;
}
// Printing all the elements of the heap
cout << "Elements of the heap are: ";
for (int i = 0; i < heap_size; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
// Function to search in a heap using linear search
int search_in_heap(int arr[], int key_value)
{
// If heap size is not equal to zero.
if (heap_size != 0)
{
// Traversing all the elements of the heap.
for (int i = 0; i < heap_size; i++)
{
if (key_value == arr[i])
{
// If element is found.
return i;
}
}
}
// If element is not found.
return -1;
}
// Driver function
int main()
{
cout << "Enter the maximum size of the heap: ";
// Asking for the maximum size of the heap
cin >> heap_max_size;
// Creating an array of size entered by the user and initializing by 0.
// This method is called the dynamic memory allocation to an array.
int *arr = new int[heap_max_size]{0};
// Providing options to an user to perform its desire action.
cout << "Enter 1 to insert an element in a heap: " << endl;
cout << "Enter 2 to delete an element from the heap: " << endl;
cout << "Enter 3 to search an element in the heap: " << endl;
cout << "Enter 4 to print all the elements of the heap: " << endl;
cout << "Enter 5 to exit from the program: " << endl;
int choice, key_value, element_found;
do
{
// Asking for the choice
cout << "Enter your choice: ";
cin >> choice;
switch (choice)
{
// If choice is to insert an element
case 1:
cout << "Enter the value to insert in a heap: ";
cin >> key_value;
insert(arr, key_value);
break;
// If choice is to delete an element
case 2:
delete_root_node(arr);
break;
case 3:
cout << "Enter the value to search in the heap: ";
cin >> key_value;
element_found = search_in_heap(arr, key_value);
element_found > -1 ? cout << "Element is found at index = " << i << endl : cout << "The element is not present in the heap!" << endl;
break;
// If choice is to traverse all elements.
case 4:
heap_traversal(arr);
break;
// If the user wants to exit from the program
case 5:
cout << "Exited Successfully!";
break;
// In case of wrong inputs
default:
cout << "Wrong choice!" << endl;
break;
}
} while (choice != 5); // Condition to exit from the program
return 0;
}
The sample output of the above program is given below:
Enter the maximum size of the heap: 15
Enter 1 to insert an element in a heap:
Enter 2 to delete an element from the heap:
Enter 3 to search an element in the heap:
Enter 4 to print all the elements of the heap:
Enter 5 to exit from the program:
// Output of inserting elements
Enter your choice: 1
Enter the value to insert in a heap: 6
Enter your choice: 1
Enter the value to insert in a heap: 7
Enter your choice: 1
Enter the value to insert in a heap: 3
Enter your choice: 1
Enter the value to insert in a heap: 5
Enter your choice: 1
Enter the value to insert in a heap: 10
Enter your choice: 1
Enter the value to insert in a heap: 4
Enter your choice: 1
Enter the value to insert in a heap: 1
// Output of traversal
Enter your choice: 4
Elements of the heap are: 1 5 3 7 10 6 4
// Output of searching
Enter your choice: 3
Enter the value to search in the heap: 10
Element is found at index = 4
Enter your choice: 3
Enter the value to search in the heap: 22
The element is not present in the heap!
// Output of deleting root node
Enter your choice: 2
Enter your choice: 4
Elements of the heap are: 3 5 4 7 10 6
Enter your choice: 5
Exited Successfully!
- Insertion in min-heap – The code of the insertion in min-heap is explained below:
void build_min_heap(int arr[], int child_index)
{
if (child_index != 0)
{
int parent_index = parent_node(child_index);
if (arr[child_index] < arr[parent_index])
{
swap(arr[child_index], arr[parent_index]);
build_min_heap(arr, parent_index);
}
}
}
void insert(int arr[], int key_value)
{
heap_size += 1;
arr[heap_size - 1] = key_value;
build_min_heap(arr, heap_size - 1);
}
- Inserting 6 at index = 0 – We are adding the first element in the min-heap at index = 0. Insert function increases the heap size, adds the element at index = 0, and calls the build min-heap function at zero indexes. The function will not perform any action, and the control is again transferred to the main function.
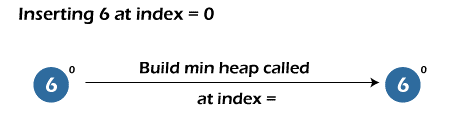
- Inserting 7 at index = 1 – Insert function increases the size of the heap by one, adds 7 at index = 0, and calls min-heap at index = 1. Here, 7 is greater than 6, which means the heap is already a min-heap. Hence, no changes will be made by the build min function.
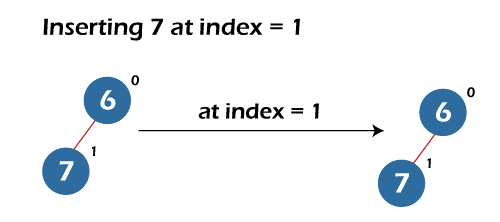
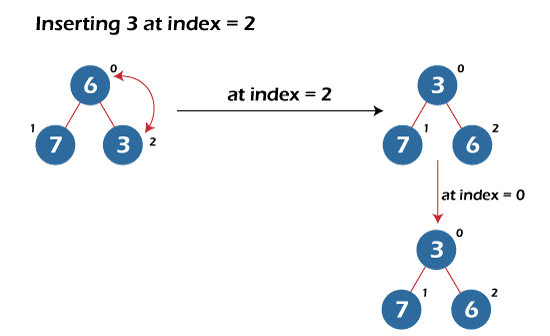
- Inserting 3 at index = 2 – Insert function again increases the size of the heap by one, adds 3 at index = 2 and calls the build min-heap function at index = 2. Here 3 is less than 6; the build min-heap function swaps both of them and calls itself at index = 0 to check whether the 3 reaches its correct position.
- Rest of the insertions are shown in the figure given below:
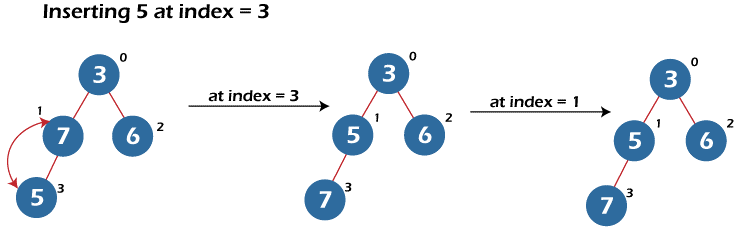
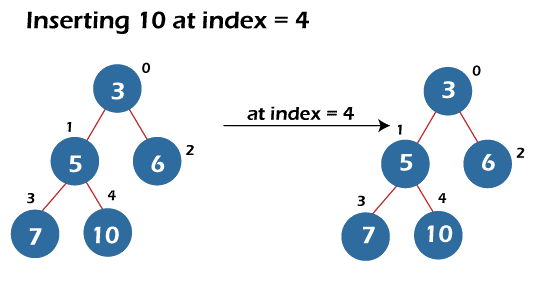
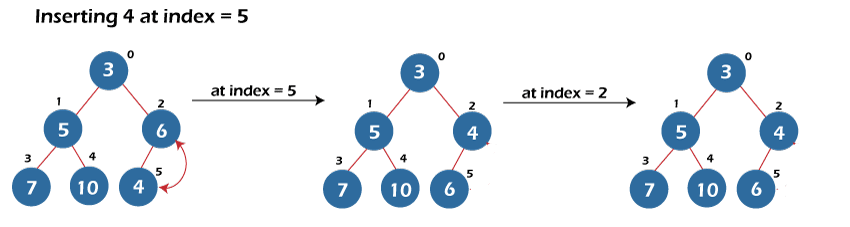
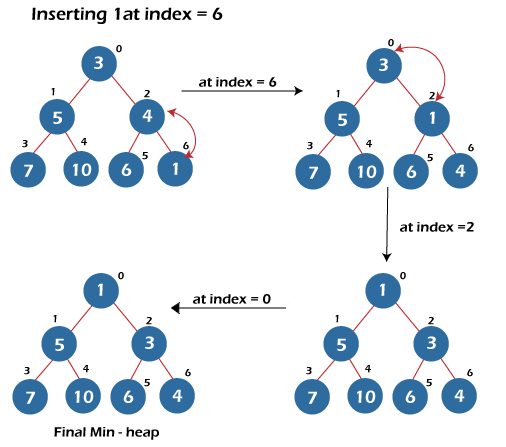
- Deletion of the root node in min-heap – The code of the deletion of the root node in min-heap is explained below:
void min_heapify(int arr[], int parent_index)
{
int left_child_index = left_child(parent_index);
int right_child_index = right_child(parent_index);
int smallest_value_index = parent_index;
if (left_child_index < heap_size && arr[left_child_index] < arr[smallest_value_index])
{
smallest_value_index = left_child_index;
}
if (right_child_index < heap_size && arr[right_child_index] < arr[smallest_value_index])
{
smallest_value_index = right_child_index;
}
if (smallest_value_index != parent_index)
{
swap(arr[smallest_value_index], arr[parent_index]);
min_heapify(arr, smallest_value_index);
}
}
void delete_root_node(int arr[])
{
int last_element = arr[heap_size - 1];
arr[0] = last_element;
heap_size -= 1;
min_heapify(arr, 0);
}
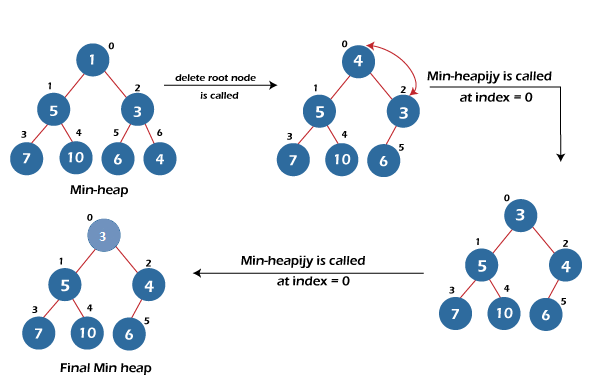
Here, the root node in the given heap is 1. The delete root node function replaces the root value with the last node value = 4, deletes the last node by decreasing the heap size by 1, and calls the min-heapify function at index 0 to re-construct the complete binary tree into a min-heap.
The min heapify function finds min of three, the root node = 4, its left child = 5, and the right child = 3. Here, the right child is the minimum; the function swaps 4 with 3 and calls itself at the index of the right child = 2. Now, 4 is correctly placed, and the obtained complete binary tree is min-heap. Hence, no changes are made by the min-heapify. And the delete function ends here, and we get our required min-heap.
The above process is also shown in the figure given below:
- Search in a heap – The heap is not optimised to search random elements; instead, it is optimised to search the largest element in max-heap and the smallest element in min-heap. This makes the searching in a heap a non-standard operation.
The time complexity of finding the minimum element in min-heap or maximum element in max-heap is O(1). To search a random element, we need to visit all the nodes, which makes its time complexity equal to O(n), the same as the time complexity of the linear search in an array.
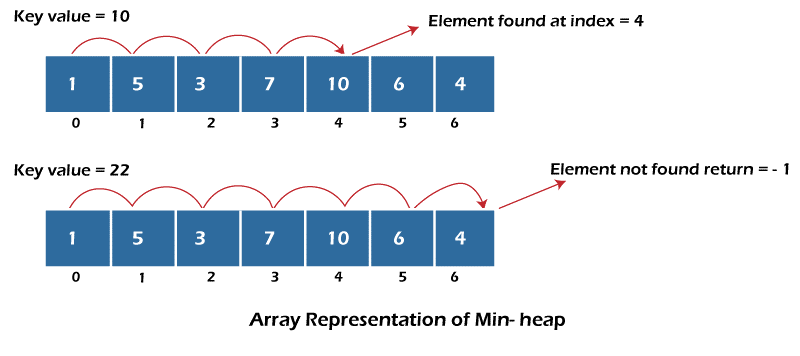
We know that the heap is implemented using an array, so for searching a random element, we implement a linear search on it. And compares it with all the values stored starting from the root index.
The code of searching in a heap, i.e., linear search in a heap, is given below:
int search_in_heap(int arr[], int key_value)
{
if (heap_size != 0)
{
for (int i = 0; i < heap_size; i++)
{
if (key_value == arr[i])
{
return i;
}
}
}
return -1;
}
In the above code, we return the element’s index if it is present in a heap or -1 if the element is not present in the heap.
- Heap Traversal – The code for traversing all the elements of a min-heap is explained below:
void heap_traversal(int arr[])
{
if (heap_size == 0)
{
cout << "No elements in the heap!" << endl;
return;
}
cout << "Elements of the heap are: ";
for (int i = 0; i < heap_size; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
In the above code, we first check whether the heap has at least one node or not. If no node is present, we return from the function. If the heap is not empty, we traverse all the nodes from zero indexes to the heap size and print the value of all nodes.