Huffman tree in Data Structures

The Huffman trees in the field of data structures are pretty impressive in their work. They are generally treated as the binary tree, which is linked with the least external route or pathway that implies the one which is linked with the least sum of the weighed pathway lengths when it comes to a given set of leaves. So, here the main agenda is to properly construct a tree that contains the least exterior path weight.

Huffman Coding

Huffman coding is generally known to be a lossless data compression algorithm. It is mainly known for its application in providing the codes to that temperament in such a way that the entire measurement of the code depends upon the frequency or mass of the succeeding character. These types of codes are specifically made of changing – lengths and that too without any adjacent character.

This implies that when we allot a given code or bit sequences to a specific character, then it is next to impossible that the same code is allocated to any other character as well. A fun fact here is that we can represent any prefix-free code as the binary tree that is full of interconnected characters occupied on the leaves. Huffman tree is initially described as the full or strict binary tree in which it is known that every leaf is fixed with a certain type of letter that is already embedded in the alphabet.

The main ideology of this type of tree is to allot changing – length codes to input characters. In this, the most persistent character attains the smallest code present there, while the least persistent character attains the largest code that is present there. This is pretty much the entire ideology on which the mechanism of the Huffman tree works and makes sure that there is no fault or uncertainty while giving the bitstream.

Example

In this section of the article, we will be taking an example to understand the concept of the Huffman tree more precisely. So, let us suppose that there are four characters present which are consecutively named w, x, y, and z, and let us assume that their succeeding variable measures are 00, 01, 0, and 1.

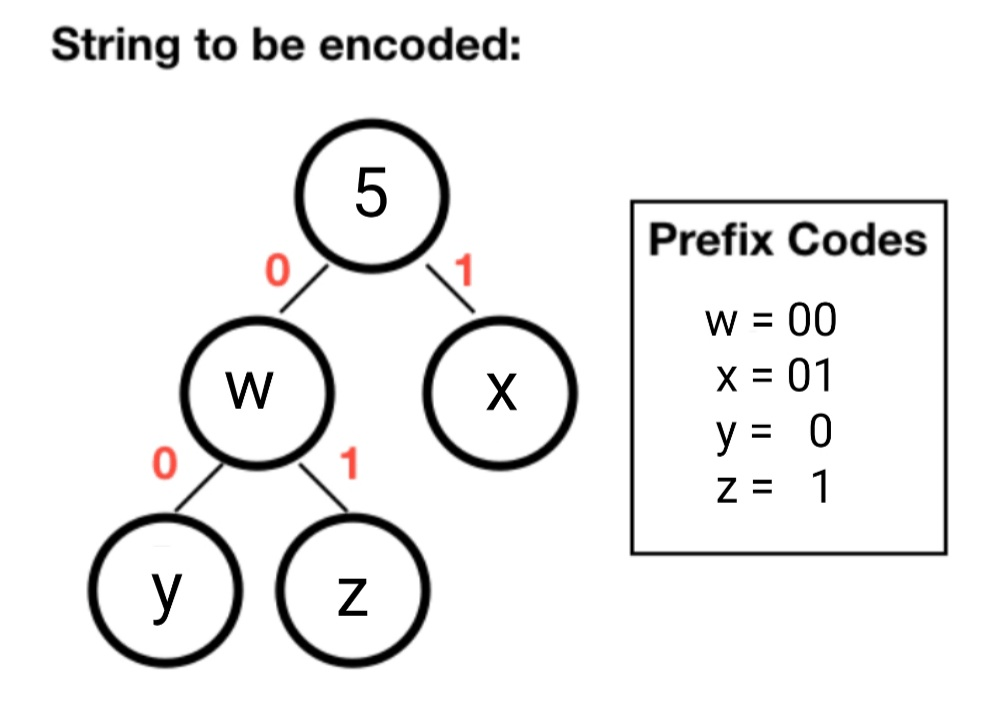
Now, if you look closely and observe, then you might realize that the codes allotted to the character y are the prefix of codes that are specifically allotted to the codes w and x. If we want to check the output of the displayed result, then it might look like this:

• The compressed bit stream will provide the result 0001
• Whereas the de – compressed bit stream will provide the result “yyyz” or “yyz” or “wyz” or “wx”.

Applications of the Huffman tree

• Huffman trees are widely used for their quick nature in fax and text propagations.
• They are quite known for their potential in generating equal outputs
• It is also used for conventional minimization of various formats such as BZIP2, GZIP, and several others.
• They are best known for their techniques in attaining entropies.

Steps to build a Huffman tree

When it comes to these kinds of trees, we mainly have to deal with two parts that are: -

• The first and very important part is to construct a Huffman tree.
• Another important aspect of the Huffman tree is learning how to traverse it.

Steps: -

1. The first and foremost task that we have to do is to build a leaf node for every character that is present. After that, we have to move ahead and construct a minimal heap of all the leaf nodes.
2. The next thing we have to do is to take out two nodes that have the minimal frequency and that too from the minimal heap.
3. Now, as we move further, we have to create a node on the inside whose frequency is equal to the sum of the two node's frequencies. After this, we can allow the two given nodes as the child of the other node. Say, the first attained node is declared as the left child, while on the other hand, the second attained node can be declared as the right child.
4. After all of this, we have to keep repeating steps number 2 and 3 until we reach a position where there is only one node present on the heap and that one single node left is also termed the root node.

Algorithm

In this section, we will be seeing the steps through which we can use a Huffman tree in data structures.

Firstly, we have to create a queue that will behave as our priority, let it be X, and it consists of unique individual characters.

Next, the following steps go for all the unique individual characters: -

1. create a newNode
2. extract minimal value from X and allot it to the left child of newNode
3. extract minimal value from X and allot it to the right child of newNode
4. We have to calculate the sum of the above two minimal values and appoint it to the value of the new node
5. We will now extract the addition of the two nodes and then, after getting the output to assign the same to the new node.
6. Return rootNode.

Implementation

In this section, we will be seeing the steps that will help us understand the working and execution of the Huffman tree.

#include <iostream>
using namespace std;


struct MinHNode {
  unsigned freq;
  char item;
  struct MinHNode *left, *right;
};


struct MinH {
  unsigned size;
  unsigned capacity;
  struct MinHNode **array;
};


//We will now create a Huffman tree
struct MinHNode *newNode(char item, unsigned freq) {
  struct MinHNode *temp = (struct MinHNode *)malloc(sizeof(struct MinHNode));


  temp->left = temp->right = NULL;
  temp->item = item;
  temp->freq = freq;


  return temp;
}


// We will now be creating a min heap 
struct MinH *createMinH(unsigned capacity) {
  struct MinH *minHeap = (struct MinH *)malloc(sizeof(struct MinH));
  minHeap->size = 0;
  minHeap->capacity = capacity;
  minHeap->array = (struct MinHNode **)malloc(minHeap->capacity * sizeof(struct MinHNode *));
  return minHeap;
}


// Printing the following
void printArray(int arr[], int n) {
  int i;
  for (i = 0; i < n; ++i)
    cout << arr[i];


  cout << "\n";
}


// Using the swap function
void swapMinHNode(struct MinHNode **a, struct MinHNode **b) {
  struct MinHNode *t = *a;
  *a = *b;
  *b = t;
}


// We will now use heapify
void minHeapify(struct MinH *minHeap, int idx) {
  int smallest = idx;
  int left = 2 * idx + 1;
  int right = 2 * idx + 2;


  if (left < minHeap->size && minHeap->array[left]->freq < minHeap->array[smallest]->freq)
    smallest = left;


  if (right < minHeap->size && minHeap->array[right]->freq < minHeap->array[smallest]->freq)
    smallest = right;


  if (smallest != idx) {
   
swapMinHNode(&minHeap->array[smallest],
           &minHeap->array[idx]);
    minHeapify(minHeap, smallest);
  }
}


//Verifying whether the size is one or not
int checkSizeOne(struct MinH *minHeap) {
  return (minHeap->size == 1);
}


// Taking out the min
struct MinHNode *extractMin(struct MinH *minHeap) {
  struct MinHNode *temp = minHeap->array[0];
  minHeap->array[0] = minHeap->array[minHeap->size - 1];


  --minHeap->size;
  minHeapify(minHeap, 0);


  return temp;
}


// Using the insertion function
void insertMinHeap(struct MinH *minHeap, struct MinHNode *minHeapNode) {
  ++minHeap->size;
  int i = minHeap->size - 1;


  while (i && minHeapNode->freq < minHeap->array[(i - 1) / 2]->freq) {
    minHeap->array[i] = minHeap->array[(i - 1) / 2];
    i = (i - 1) / 2;
  }


  minHeap->array[i] = minHeapNode;
}


// Constructing min heap
void buildMinHeap(struct MinH *minHeap) {
  int n = minHeap->size - 1;
  int i;


  for (i = (n - 1) / 2; i >= 0; --i)
    minHeapify(minHeap, i);
}


int isLeaf(struct MinHNode *root) {
  return !(root->left) && !(root->right);
}


struct MinH *createAndBuildMinHeap(char item[], int freq[], int size) {
  struct MinH *minHeap = createMinH(size);


  for (int i = 0; i < size; ++i)
    minHeap->array[i] = newNode(item[i], freq[i]);


  minHeap->size = size;
  buildMinHeap(minHeap);


  return minHeap;
}


struct MinHNode *buildHfTree(char item[], int freq[], int size) {
  struct MinHNode *left, *right, *top;
  struct MinH *minHeap = createAndBuildMinHeap(item, freq, size);


  while (!checkSizeOne(minHeap)) {
    left = extractMin(minHeap);
    right = extractMin(minHeap);


    top = newNode('$', left->freq + right->freq);


    top->left = left;
    top->right = right;


    insertMinHeap(minHeap, top);
  }
  return extractMin(minHeap);
}
void printHCodes(struct MinHNode *root, int arr[], int top) {
  if (root->left) {
    arr[top] = 0;
    printHCodes(root->left, arr, top + 1);
  }


  if (root->right) {
    arr[top] = 1;
    printHCodes(root->right, arr, top + 1);
  }
  if (isLeaf(root)) {
    cout << root->item << " | ";
    printArray(arr, top);
  }
}


//Using the wrapper function
void HuffmanCodes(char item[], int freq[], int size) {
  struct MinHNode *root = buildHfTree(item, freq, size);


  int arr[MAX_TREE_HT], top = 0;


  printHCodes(root, arr, top);
}


int main() {
  char arr[] = {'A', 'B', 'C', 'D'};
  int freq[] = {5, 1, 6, 3};


  int size = sizeof(arr) / sizeof(arr[0]);


  cout << "Char | Huffman code ";
  cout << "\n----------------------\n";
  HuffmanCodes(arr, freq, size);
}

Output: