Program to calculate the area of the circumcircle of an equilateral triangle

You have given one value which represents the side of the equilateral triangle. You have to find out the area of the circumcircle. Let’s take an example -

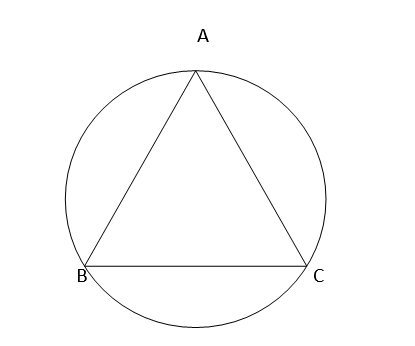
For the above diagram, we have an equilateral triangle named ABC. We have to find out the area of its circumcircle.

Input-

6

Output-

37.69

Explanation- 6 is the value of the side of an equilateral triangle. By calculating the area of the circumcircle, we get the answer 37.69.

Note: -

What is the equilateral triangle?

Triangle has three sides, and an equilateral triangle is a triangle whose three sides are equal. It means, according to the above diagram, the sides AB, BC, and CA are of the same length.

AB = BC = CA

What is the circumcircle?

A circumcircle is a special type of circle. For various types of polygons, we can get circumcircles. It is a circle which goes through every vertex of the polygon. We can calculate different properties of the circle by using different properties of the polygon. A circumcircle of an equilateral triangle goes through three vertices of the triangle.

Algorithm:-

Step 1: Start

Step 2: The value of the sides of a triangle is taken from the user

Step 3: A function is called to calculate the area.

Step 4: In this function, we take the input value, which represents the side of the triangle.

Step 5: The floating point variable is declared in function to store the area

Step 6: The area is calculated.

Step 7: The value of the calculated area is returned.

Step 8: The returned value will be printed.

Step 9: Stop.

Explanation of Algorithm: - Let's try to understand the algorithm by the above diagram. We have an equilateral triangle ABC whose each side is the same in length ( AB = BC = CA ). If we consider the point 'O' as the centre of the circle that goes through each vertex of the triangle, then the value of OA is the radius of the circle. From geometry, we know that the intersection point of all medians of a triangle is the centre of the circumcircle of the equilateral triangle. In this way, we can get the value of the radius of the circle based on the side of the triangle. So, radius = a/ ( root of 3 ).

The formula of area of circle is

Here r = a/

So, area =

Code: -

// Program in CPP to calculate the area of circum.
Circle of an equilateral triangle
#include <iostream>
#include <math.h>
using namespace std;
// function to calculate the area of circumcircle
// of equilateral triangle
float area_circumscribed(float a)
{
	return (a * a * (3.14 / 3));
}
// Driver code
int main()
{
	float a, Area;
	cin >> a;
	// function calling
	Area = area_circumscribed(a);
	// displaying the area
	cout << " The value of triangle side = " << a;
cout << “Area of CircumCircle = ”  << Area;
	return 0;
}

Program in C

// Program in c to calculate the area of circum
circle of an equilateral triangle
#include <stdio.h>
#define PI 3.14159265
// function to find area of
// circumscribed circle
float area_circumscribed(float a)
{
	return (a * a * (PI / 3));
}
// Driver code
int main()
{
	float a = 6;
	printf("Area of circumscribed circle is :%f",
			area_circumscribed(a));
	return 0;
}

Program in Java

// Program in java to calculate the area of the circum
circle of an equilateral triangle
import java. lang.*;
class jtp {	
	static double PI = 3.14159265;
	// function to find the area of
	// circumscribed circle
	public static double area_circumscribed(double a)
	{
		return (a * a * (PI / 3));
	}
	// Driver code
	public static void main(String[] args)
	{
		double a = 6.0;
		System.out.println("Area of circumscribed circle is :"
		+ area_circumscribed(a));
	}
}

Program in Python

// Program in python to calculate the area of the circum
circle of an equilateral triangle
PI = 3.14159265	
# Function to find the area of
# circumscribed circle
def area_circumscribed(a):
	return (a * a * (PI / 3))	
# Driver code
a = 6.0
print("Area of circumscribed circle is :%f"
       %area_circumscribed(a))

Output:

1.	 The value of triangle side = 6
Area of CircumCircle = 37.69
2.	The value of triangle side = 9
Area of CircumCircle = 84.82
3.	The value of triangle side = 3
Area of CircumCircle = 9.42

Complexity Analysis: -

Time complexity- Here, we need no recursion or looping so we can find the solution within constant time. Time complexity will be O (1).

Space complexity- In this solution, we use constant memory. So, space complexity will be O(1).