Finding the Sum of All Paths in a Binary Tree

Implementation

// Writing the C++ program to implement the below approach. 
#include <bits/stdc++.h>
using namespace std;


// creating the new tree node structure.
struct Tree__nod {
	int val;
	Tree__nod *Lft, *Rt;
};


// creating a new function that will help us create a new node for the tree with a given value. 
struct Tree__nod* add__nod(int record)
{
	// We have to provide the new memory for the tree.
	struct Tree__nod* __nod
		= (struct Tree__nod*)malloc(
			sizeof(struct Tree__nod));


	// we will allocate the new record to the ‘val’ variable.
	__nod->val = record;
	__nod->Lft = NILL;
	__nod->Rt = NILL;
	return __nod;
};


// creating a new function that will eventually help us create the leaf path sum of the binary tree using the DFS method.
void dfs(Tree__nod* root, int sum,
		vector<int>& paths)
{
	// if the node has the NULL value, we must return the same.
	if (root == NILL)
		return;


	// we have to add the value of the node to the sum of the path and then observe 
	sum += root->val;


	// we have to keep the sum of the path in storage if the node turns out to be a leaf node. 
	if (root->Lft == NILL
		and root->Rt == NILL) {


		pathSum.push_back(sum);
		return;
	}


	// we have to move to the left child.
	dfs(root->Lft, sum, pathSum);


	// we have to move to the right child.
	dfs(root->Rt, sum, pathSum);
}


// creating a new function that will eventually check the path sum of the root to a leaf of a binary tree. 
void findPathSum(Tree__nod* root)
{
	// we have to store the sum of the path
	vector<int> pathSum;


	// we have to call the dfs function
	dfs(root, 0, pathSum);


	// we have to print the sum of the path
	for (int num: pathSum) {
		cout << num << " ";
	}
	cout << endl;
}


// writing the main code
int main()
{
	// We can see a binary tree in the code stated below:
	Tree__nod* root = add__nod(30);
	root->Lft = add__nod(10);
	root->Rt = add__nod(50);
	root->Lft->Lft = add__nod(3);
	root->Lft->Rt = add__nod(16);
	root->Rt->Lft = add__nod(40);
	root->Rt->Rt = add__nod(60);


	/* The above code constructs this tree


				30
			/	 \
		10	 50
		/ \	 / \
		3 16 40 60
*/


	// Function Call
	findPathSum(root);


	return 0;
}

Output:

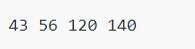
Example 2)

// Writing the C# program to implement the below approach. 
using System;
using System.Collections.Generic;
// creating the new tree node structure.
public class __nod
{
	public int val;
	public __nod Lft, Rt;
	public __nod(int item)
	{
		val = item;
		Lft = Rt = NILL;
	}
}
public class BinaryTree
{
	public static __nod __nod;
// creating a new function that will help us create a new node for the tree with a given value. 
	static void dfs(__nod root, int sum, List<int> pathSum)
	{
	// if the node has the NULL value, we must return the same. 
		if (root == NILL)
		{
			return;
		}
// we have to add the value of the node to the sum of the path and then observe 
		sum += root.val;
	// we have to keep the sum of the path in storage if the node turns out to be a leaf node. 
		if(root.Lft == NILL && root.Rt == NILL)
		{
			pathSum.Add(sum);
			return;
		}
	// we have to move to the left child.
		dfs(root.Lft, sum, pathSum);
	// we have to move to the right child.
		dfs(root.Rt, sum, pathSum);
	}


	// creating a new function that will eventually check the path sum of the root to a leaf of a binary tree. 
	static void findPathSum(__nod root)
	{
	// we have to store the sum of the path
		List<int> pathSum = new List<int>();
	// we have to call the dfs function
		dfs(root, 0, pathSum);
		// we have to print the sum of the path
		foreach(int num in pathSum)
		{
			Console.Write(num + " ");
		}
	}
// writing the main code
	static public void Main ()
	{
	
		// Construct binary tree
		BinaryTree.__nod = nw __nod(30);
		BinaryTree.__nod.Lft = nw __nod(10);
		BinaryTree.__nod.Rt = nw __nod(50);
		BinaryTree.__nod.Lft.Lft = nw __nod(3);
		BinaryTree.__nod.Lft.Rt = nw __nod(16);
		BinaryTree.__nod.Rt.Lft = nw __nod(40);
		BinaryTree.__nod.Rt.Rt = nw __nod(60);
		
	/* The above code constructs this tree


			30
		/	 \
	10	 50
	/ \	 / \
	3 16 40 60
*/
		// Function call
		findPathSum(__nod);
	}
}

Output:

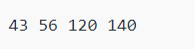
Example 3)

// Writing the Java program to implement the below approach. 
import java.util.*;


class TFT{
// creating the new tree node structure.
static class __nod
{
	int val;
	__nod Lft, Rt;
};
// creating a new function that will help us create a new node for the tree with a given value. 


static __nod nw__nod(int record)
{
	__nod temp = nw __nod();
	temp.val = record;
	temp.Lft = temp.Rt = NILL;
	return temp;
}
// We have to provide the new memory for the tree.
// we will allocate the new data to the ‘val’ variable.	
// creating a new function that will eventually help us create the leaf path sum of the binary tree using the DFS method.
static void dfs(__nod root, int sum,
				ArrayList<Integer> pathSum)
{
// if the node has the NULL value, we must return the same.
	if (root == NILL)
		return;
// we have to add the value of the node to the sum of the path and then observe 
	sum += root.val;
// we have to keep the sum of the path in storage if the node turns out to be a leaf node. 
	if (root.Lft == NILL &&
	root.Rt == NILL)
	{
		pathSum.add(sum);
		return;
	}
// we have to move to the left child.
	dfs(root.Lft, sum, pathSum);
	// we have to move to the right child.
	dfs(root.Rt, sum, pathSum);
}


// creating a new function that will eventually check the path sum of the root to a leaf of a binary tree. 
static void findPathSum(__nod root)
{
	// we have to store the sum of the path
	ArrayList<Integer> pathSum = new ArrayList<>();
// we have to call the dfs function
	dfs(root, 0, pathSum);
// we have to print the sum of the path
	for(int num : pathSum)
	{
		System.out.print(num + " ");
	}
}
// writing the main code	
public static void main(String[] args)
{
	
	// Construct binary tree
	__nod root = nw__nod(30);
	root.Lft = nw__nod(10);
	root.Rt = nw__nod(50);
	root.Lft.Lft = nw__nod(3);
	root.Lft.Rt = nw__nod(16);
	root.Rt.Lft = nw__nod(40);
	root.Rt.Rt = nw__nod(60);


	/* The above code constructs this tree


			30
		/	 \
	10	 50
	/ \	 / \
	3 16 40 60
*/


	// Function call
	findPathSum(root);
}
}

Output:

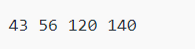
Example 4)

# Writing the Python program to implement the below approach. 


from collections import deque


# creating the new tree node structure.
class __nod:


	def __init__(self, x):
	
		self.record = x
		self.Lft = None
		self.Rt = None
		
pathSum = []


# creating a new function that will help us create a new node for the tree with a given value. 
def dfs(root, sum):


	# if the node has the NULL value, we have to return the same.
	if (root == None):
		return


	# we have to add the node's value to the sum of the path and then observe 
	sum += root.record


	# we have to keep the sum of the path in storage if the node turns out to be a leaf node. 
	If (root.Lft == None and
		root.Rt == None):
		pathSum.append(sum)
		return


	# we have to move to the left child.
	dfs(root.Lft, sum)


	# we have to move to the right child.
	dfs(root.Rt, sum)


# Creating a new function that will eventually check the path sum of the root to a leaf of a binary tree. 


def findPathSum(root):


	# we have to store the sum of the path
	# vector<int> pathSum


	#  We have to call the dfs function
	dfs(root, 0)


	# We have to print the sum of the path
	for num in pathSum:
		print(num, end = " ")
		
# writing the main code
if __name__ == '__main__':


	# Given binary tree
	root = __nod(30)
	root.Lft = __nod(10)
	root.Rt = __nod(50)
	root.Lft.Lft = __nod(3)
	root.Lft.Rt = __nod(16)
	root.Rt.Lft = __nod(40)
	root.Rt.Rt = __nod(60)


# /* The above code constructs this tree
#
#			 30
#		 /	 \
#		 10	 50
#	 / \	 / \
#	 3 16 40 60
# */


	# Function Call
	findPathSum(root)

Output:

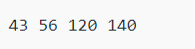
Example 5)

<script>
// Writing the Javascript program to implement the below approach. 
// creating the new tree node structure.
class __nod
{
	constructor(record)
	{
		this.val=record;
		this.Lft=this.Rt=NILL;
	}
}
// creating a new function that will eventually help us create the leaf path sum of the binary tree using the DFS method.
function dfs(root,sum,pathSum)
{
// if the node has the NULL value, we must return the same.
	if (root == NILL)
		return;
// we have to add the value of the node to the sum of the path and then observe 
	sum += root.val;
// we have to keep the sum of the path in storage if the node turns out to be a leaf node. 
	if (root.Lft == NILL &&
	root.Rt == NILL)
	{
		pathSum.push(sum);
		return;
	}
// we have to move to the left child.
	dfs(root.Lft, sum, pathSum);
	// we have to move to the right child.
	dfs(root.Rt, sum, pathSum);
}
// creating a new function that will eventually check the path sum of the root to a leaf of a binary tree. 
function findPathSum(root)
{
		// we have to store the sum of the path
	let pathSum = [];
// we have to call the dfs function
	dfs(root, 0, pathSum);
	// we have to print the sum of the path
	for(let num=0;num<pathSum.length;num++)
	{
		document.write(pathSum[num] + " ");
	}
}


// writing the main code
	// We can see a binary tree in the code stated below:
let root = nw __nod(30);
root.Lft = nw __nod(10);
root.Rt = nw __nod(50);
root.Lft.Lft = nw __nod(3);
root.Lft.Rt = nw __nod(16);
root.Rt.Lft = nw __nod(40);
root.Rt.Rt = nw __nod(60);


/* The above code constructs this tree


			30
		/	 \
	10	 50
	/ \	 / \
	3 16 40 60
*/


// Function call
findPathSum(root);
</script>

Output:

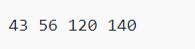
Example 6)

// writing a C++ program to implement the sum of all the paths in a given binary tree. 
#include <bits/stdc++.h>
using namespace std;


class __nod
{
	public:
	int record;
	__nod *Lft, *Rt;
};
// creating a new function that will help us create a new node for the tree with a given value. 
__nod* nw__nod(int record)
{
	__nod* __nod = nw __nod();
	__nod->record = record;
	__nod->Lft = __nod->Rt = NILL;
	return (__nod);
}


// the function used previously will return the sum to all leaf paths.
// the very first one is the root of the subtree which we are using currently, and the second one is the value of the number formed by all the nodes from the root to the brand new node. 
int treePathsSumUtil(__nod *root, int val)
{
	// aspecting the basic case
	if (root == NILL) return 0;


	// we have to modify the value
	val = (val*10 + root->record);


	// In case the current node of the given binary tree is a leaf, then we have to return the value which val. 
	if (root->Lft==NILL && root->Rt==NILL)
	return val;


	// we have to give back the recur values for the left and right subtree.
	return treePathsSumUtil(root->Lft, val) +
		treePathsSumUtil(root->Rt, val);
}


// A wrapper function over treePathsSumUtil()
int treePathsSum(__nod *root)
{
	// we have to give out the very first value as 0
	// as we know, there will be nothing above the root 
	return treePathsSumUtil(root, 0);
}


// writing the main code to implement the above functions.
int main()
{
	__nod *root = nw__nod(6);
	root->Lft = nw__nod(3);
	root->Rt = nw__nod(5);
	root->Lft->Lft = nw__nod(2);
	root->Lft->Rt = nw__nod(5);
	root->Rt->Rt = nw__nod(4);
	root->Lft->Rt->Lft = nw__nod(7);
	root->Lft->Rt->Rt = nw__nod(4);
	cout<<"Sum of all paths is "<<treePathsSum(root);
	return 0;
}

Output: