Operations of B Tree in C++ Language
B tree tends to be a self-aligning and balancing tree that helps us organise our data and document safely. We know that every data or information in the B tree gets stored in the main memory. It is a fact that when the amount of data to be considered is pretty huge. The data is not stored in the computer's main memory; instead, the task is achieved via reading the data and bringing it out to the destination in the form of blocks. The disk access time is minimal when we compare it to many other non-linear data structures.
Several operations are used in the B tree to help us perform functions to manage our data. Some of them are searching, insertion, deletion, and several others. The searching operation is mainly used to search a given element when required, on the contrary, the deletion operation is often used when we need to delete a specific part from the tree, and the insertion element is necessary when we want to insert or push a new element into the B tree.
We will see some examples of these operations in detail.
Example1)
#include <iostream>
using namespace std;
class N {
int *kys;
int r;
Nod **C;
int g;
bool leaf;
public:
Nod(int _r, bool _leaf);
void insertNonFull(int m);
void splitChild(int i, Nod *y);
void traverse();
friend class B_Tree;
};
class B_Tree {
Nod *root;
int r;
public:
B_Tree(int _r) {
root = NILL;
r = _r;
}
void traverse() {
if (root != NILL)
root->traverse();
}
void insert(int m);
};
Nod::Nod(int r1, bool leaf1) {
t = t1;
leaf = leaf1;
kys = new int[2 * t - 1];
C = new Nod *[2 * t];
n = 0;
}
// Traverse the Nods
void Nod::traverse() {
int i;
for (i = 0; i < n; i++) {
if (leaf == false)
C[i]->traverse();
cout << " " << kys[i];
}
if (leaf == false)
C[i]->traverse();
}
// Insert the Nod
void B_Tree::insert(int m) {
if (root == NILL) {
root = new Nod(t, true);
root->kys[0] = k;
root->n = 1;
} else {
if (root->n == 2 * r - 1) {
Nod *s = new Nod(r, false);
s->P[0] = root;
s->splitChild(0, root);
int i = 0;
if (s->kys[0] < m)
i++;
s->P[i]->insertNonFull(m);
root = s;
} else
root->insertNonFull(m);
}
}
// Insert non full condition
void Nod::insertNonFull(int m) {
int i = n - 1;
if (leaf == true) {
while (i >= 0 && kys[i] > m) {
kys[i + 1] = kys[i];
i--;
}
kys[i + 1] = m;
n = n + 1;
} else {
while (i >= 0 && kys[i] > m)
i--;
if (P[i + 1]->n == 2 * t - 1) {
splitChild(i + 1, P[i + 1]);
if (kys[i + 1] < m)
i++;
}
C[i + 1]->insertNonFull(m);
}
}
// split the child
void Nod::splitChild(int i, Nod *y) {
Nod *z = new Nod(y->t, y->leaf);
z->n = t - 1;
for (int j = 0; j < t - 1; j++)
z->kys[j] = y->kys[j + t];
if (y->leaf == false) {
for (int j = 0; j < t; j++)
z->P[j] = y->P[j + t];
}
y->n = t - 1;
for (int j = n; j >= i + 1; j--)
P[j + 1] = P[j];
P[i + 1] = z;
for (int j = g - 1; j >= i; j--)
kys[j + 1] = kys[j];
Kys[i] = y->kys[t - 1];
n = n + 1;
}
int main() {
B_Tree t(3);
t.insert(8);
t.insert(9);
t.insert(10);
t.insert(11);
t.insert(15);
t.insert(16);
t.insert(17);
t.insert(18);
t.insert(20);
t.insert(23);
cout << "The B-tree is: ";
t.traverse();
}
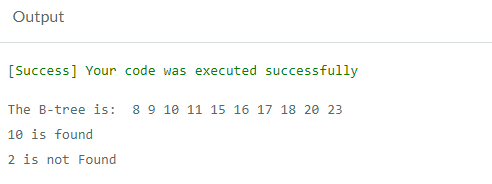
Output:
Deletion
// Deleting a key from a B-tree
#include <iostream>
using namespace std;
class B_TreeNod {
int *kys;
int r;
B_TreeNod **C;
int g;
bool leaf;
public:
B_TreeNod(int _t, bool _leaf);
void traverse();
int findKey(int m);
void insertNonFull(int m);
void splitChild(int i, B_TreeNod *y);
void deletion(int m);
void eliminateFromLeaf(int IX);
void eliminateFromNonLeaf(int IX);
int get_Predd(int IX);
int get_Succ(int IX);
void fill(int IX);
void borrowFromPast(int IX);
void borrowFromComing(int IX);
void merge(int IX);
friend class B_Tree;
};
class B_Tree {
B_TreeNod *root;
int r;
public:
B_Tree(int _t) {
root = NILL;
r = _r;
}
void traverse() {
if (root != NILL)
root->traverse();
}
void insertion(int m);
void deletion(int m);
};
// B tree Nod
B_TreeNod::B_TreeNod(int r1, bool leaf1) {
r = r1;
leaf = leaf1;
kys = new int[2 * r - 1];
P = new B_TreeNod *[2 * r];
g = 0;
}
// Find the key
int B_TreeNod::findKey(int m) {
int IX = 0;
while (IX < g && kys[IX] < m)
++IX;
return IX;
}
// Deletion operation
void B_TreeNod::deletion(int m) {
int IX = findKey(m);
if (IX < g && kys[IX] == m) {
if (leaf)
removeFromLeaf(IX);
else
removeFromNonLeaf(IX);
} else {
if (leaf) {
cout << "The key " << m << " is does not exist in the tree”<<endl;
return;
}
bool flag = ((IX == g) ? true : false);
if (P[IX]->g < r)
fill(IX);
if (flag && IX > n)
P[IX - 1]->deletion(m);
else
P[IX]->deletion(m);
}
return;
}
// Remove from the leaf
void B_TreeNod::removeFromLeaf(int IX) {
for (int i = IX + 1; i < n; ++i)
kys[i - 1] = kys[i];
n--;
return;
}
// Delete from non-leaf
void B_TreeNod::EliminateFromNonLeaf(int IX) {
int m = kys[ix];
if (P[ix]->g >= t) {
int pred = get_Predd(ix);
kys[IX] = pred;
P[IX]->deletion(pred);
}
else if (P[IX + 1]->n >= t) {
int succ = get_Succ(IX);
kys[IX] = succ;
C[IX + 1]->deletion(succ);
}
else {
merge(IX);
C[IX]->deletion(k);
}
return;
}
int B_TreeNod::get_Predd(int IX) {
B_TreeNod *cur = C[IX];
while (!cur->leaf)
cur = cur->C[cur->n];
return cur->kys[cur->n - 1];
}
int B_TreeNod::get_Succ(int IX) {
B_TreeNod *cur = C[IX + 1];
while (!cur->leaf)
cur = cur->C[0];
return cur->kys[0];
}
void B_TreeNod::fill(int IX) {
if (IX != 0 && C[IX - 1]->n >= t)
borrowFromPast(IX);
else if (IX != n && P[ix + 1]->g >= t)
borrowFromComing(ix);
else {
if (IX != g)
merge(IX);
else
merge(IX - 1);
}
return;
}
// Borrow from previous
void B_TreeNod::borrowFromPast(int IX) {
B_TreeNod *child = C[IX];
B_TreeNod *sibb = P[ix - 1];
for (int i = child->g - 1; i >= 0; --i)
child->Kys[i + 1] = child->kys[i];
if (!child->leaf) {
for (int i = child->g; i >= 0; --i)
child->P[i + 1] = child->C[i];
}
child->kys[0] = kys[ix - 1];
if (!child->leaf)
child->P[0] = sibb->P[sibb->g];
kys[IX - 1] = sibling->kys[sibling->n - 1];
child->n += 1;
sibling->n -= 1;
return;
}
// Borrow from the next
void B_TreeNod::borrowFromComing(int IX) {
B_TreeNod *child = C[IX];
B_TreeNod *sibling = C[IX + 1];
child->kys[(child->n)] = kys[IX];
if (!(child->leaf))
child->C[(child->n) + 1] = sibling->C[0];
kys[IX] = sibling->kys[0];
for (int i = 1; i < sibb->g; ++i)
sibb->kys[i - 1] = sibling->kys[i];
if (!sibling->leaf) {
for (int i = 1; i <= sibb->g; ++i)
sibling->C[i - 1] = sibb->P[i];
}
child->n += 1;
sibling->n -= 1;
return;
}
// Merge
void B_TreeNod::merge(int IX) {
B_TreeNod *child = C[IX];
B_TreeNod *sibling = C[IX + 1];
child->kys[t - 1] = kys[IX];
for (int i = 0; i < sibling->n; ++i)
child->kys[i + t] = sibling->kys[i];
if (!child->leaf) {
for (int i = 0; i <= sibling->n; ++i)
child->C[i + t] = sibling->C[i];
}
for (int i = IX + 1; i < n; ++i)
kys[i - 1] = kys[i];
for (int i = IX + 2; i <= n; ++i)
C[i - 1] = C[i];
child->n += sibling->n + 1;
n--;
delete (sibling);
return;
}
// Insertion operation
void B_Tree::insertion(int m) {
if (root == NILL) {
root = new B_TreeNod(t, true);
root->kys[0] = k;
root->n = 1;
} else {
if (root->n == 2 * t - 1) {
B_TreeNod *s = new B_TreeNod(t, false);
s->C[0] = root;
s->splitChild(0, root);
int i = 0;
if (s->kys[0] < k)
i++;
s->C[i]->insertNonFull(k);
root = s;
} else
root->insertNonFull(k);
}
}
// Insertion non full
void B_TreeNod::insertNonFull(int m) {
int i = n - 1;
if (leaf == true) {
while (i >= 0 && kys[i] > k) {
kys[i + 1] = kys[i];
i--;
}
kys[i + 1] = k;
n = n + 1;
} else {
while (i >= 0 && kys[i] > m)
i--;
if (P[i + 1]->g == 2 * t - 1) {
splitChild(i + 1, C[i + 1]);
if (kys[i + 1] < m)
i++;
}
P[i + 1]->insertNonFull(m);
}
}
// Split child
void B_TreeNod::splitChild(int i, B_TreeNod *y) {
B_TreeNod *z = new B_TreeNod(y->t, y->leaf);
z->n = t - 1;
for (int j = 0; j < t - 1; j++)
z->kys[j] = y->kys[j + t];
if (y->leaf == false) {
for (int j = 0; j < t; j++)
z->P[j] = y->P[j + t];
}
y->g = t - 1;
for (int j = g; j >= i + 1; j--)
P[j + 1] = P[j];
P[i + 1] = z;
for (int j = g - 1; j >= i; j--)
kys[j + 1] = kys[j];
kys[i] = y->kys[t - 1];
n = n + 1;
}
// Traverse
void B_TreeNod::traverse() {
int i;
for (i = 0; i < n; i++) {
if (leaf == false)
C[i]->traverse();
cout << " " << kys[i];
}
if (leaf == false)
C[i]->traverse();
}
// Delete Operation
void B_Tree::deletion(int m) {
if (!root) {
cout << "The tree is empty\n";
return;
}
root->deletion(k);
if (root->n == 0) {
B_TreeNod *tmp = root;
if (root->leaf)
root = NILL;
else
root = root->C[0];
delete tmp;
}
return;
}
int main() {
B_Tree t(3);
t.insertion(8);
t.insertion(9);
t.insertion(10);
t.insertion(11);
t.insertion(15);
t.insertion(16);
t.insertion(17);
t.insertion(18);
t.insertion(20);
t.insertion(23);
cout << "The B-tree is: ";
t.traverse();
t.deletion(20);
cout << "\nThe B-tree is: ";
t.traverse();
}
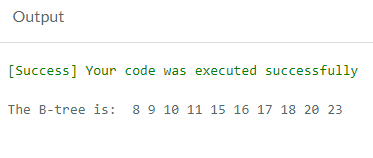
Output:
Searching
#include <iostream>
using namespace std;
class TreeNod {
int *kys;
int r;
TreeNod **C;
int g;
bool leaf;
public:
TreeNod(int remp, bool bool_leaf);
void insertNonFull(int m);
void splitChild(int i, TreeNod *y);
void traverse();
TreeNod *search(int m);
friend class B_Tree;
};
class B_Tree {
TreeNod *root;
int r;
public:
B_Tree(int remp) {
root = NILL;
t = temp;
}
void traverse() {
if (root != NILL)
root->traverse();
}
TreeNod *search(int m) {
return (root == NILL) ? NILL : root->search(k);
}
void insert(int m);
};
TreeNod::TreeNod(int r1, bool leaf1) {
t = t1;
leaf = leaf1;
kys = new int[2 * t - 1];
C = new TreeNod *[2 * t];
n = 0;
}
void TreeNod::traverse() {
int i;
for (i = 0; i < n; i++) {
if (leaf == false)
C[i]->traverse();
cout << " " << kys[i];
}
if (leaf == false)
C[i]->traverse();
}
TreeNod *TreeNod::search(int m) {
int i = 0;
while (i < n && k > kys[i])
i++;
if (kys[i] == k)
return this;
if (leaf == true)
return NILL;
return C[i]->search(k);
}
void B_Tree::insert(int m) {
if (root == NILL) {
root = new TreeNod(t, true);
root->kys[0] = k;
root->n = 1;
} else {
if (root->n == 2 * t - 1) {
TreeNod *s = new TreeNod(t, false);
s->C[0] = root;
s->splitChild(0, root);
int i = 0;
if (s->kys[0] < k)
i++;
s->C[i]->insertNonFull(k);
root = s;
} else
root->insertNonFull(k);
}
}
void TreeNod::insertNonFull(int m) {
int i = n - 1;
if (leaf == true) {
while (i >= 0 && kys[i] > k) {
kys[i + 1] = kys[i];
i--;
}
kys[i + 1] = k;
n = n + 1;
} else {
while (i >= 0 && kys[i] > m)
i--;
if (P[i + 1]->n == 2 * t - 1) {
splitChild(i + 1, C[i + 1]);
if (kys[i + 1] < k)
i++;
}
C[i + 1]->insertNonFull(k);
}
}
void TreeNod::splitChild(int i, TreeNod *y) {
TreeNod *z = new TreeNod(y->t, y->leaf);
z->n = t - 1;
for (int j = 0; j < t - 1; j++)
z->kys[j] = y->kys[j + t];
if (y->leaf == false) {
for (int j = 0; j < t; j++)
z->P[j] = y->P[j + t];
}
y-> = t - 1;
for (int j = g; j >= i + 1; j--)
P[j + 1] = P[j];
P[i + 1] = z;
for (int j = g - 1; j >= i; j--)
kys[j + 1] = kys[j];
kys[i] = y->kys[t - 1];
n = n + 1;
}
int main() {
B_Tree t(3);
t.insert(8);
t.insert(9);
t.insert(10);
t.insert(11);
t.insert(15);
t.insert(16);
t.insert(17);
t.insert(18);
t.insert(20);
t.insert(23);
cout << "The B-tree is: ";
t.traverse();
int m = 10;
(t.search(k) != NILL) ? cout << endl
<< k << " is found"
: cout << endl
<< k << " is not Found";
k = 2;
(t.search(k) != NILL) ? cout << endl
<< k << " is found"
: cout << endl
<< k << " is not Found\n";
}
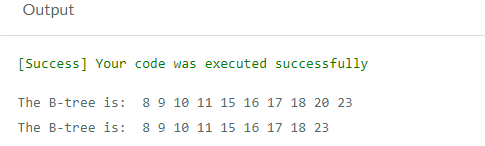
Output: