Introduction to Arrays

What exactly is an array?

A group of related data pieces stored in contiguous memory regions is referred to as an array. It is the most basic data structure in which each data piece may be retrieved simply by its index number alone.

For example, if we want to keep a student's grades in five subjects, we don't need to establish distinct variables for each topic. We may instead build an array that stores the data items in contiguous memory regions.

Array marks[5] denotes the marks scored by a student in 5 different subjects, where each subject marks are located at a specific location in the array, i.e. marks[0] denotes the marks scored in the first subject, marks[1] denotes the marks scored in the second subject, and so on and so forth.

The objective is to group together goods of the same category. This makes calculating the position of each element easy by simply adding an offset to a base value, such as the memory address of the array's first member (generally denoted by the name of the array. Index 0 is the starting point, and the offset is the difference between the two indices.

Use of an Array Is Necessary –

In most circumstances, programming requires the storage of a huge amount of data of a comparable type. We need to establish a lot of variables to store such a large amount of data. While writing the scripts, it would be quite difficult to remember all of the variable names. It is preferable to create an array and store all of the items in it.

The following example demonstrates how arrays may be utilised in code-writing:

We've given a student's grades in five distinct disciplines in the example below. The goal is to find the average of a student's grades.

Without the use of an array –

#include<stdio.h>
void main()
{
            int sub1 = 41, sub2 = 54, sub3 = 50, sub4 = 74, sub5 = 72;
            float average = (sub1 + sub2 + sub3 + sub4 + sub5)/5;
            printf(average);
}

While array is being used –

#include<stdio.h>
void main()
{
            int subject[5]={41,54,50,74,72};
            float average = ( subject[0] + subject[1] + subject[2] + subject[3] + subject[4])/5;
            printf(average);
}

Complexities of Array Operations

Time Complexity

Algorithm	Average case	Worst case
Access	O (1)	O (1)
Search	O (n)	O (n)
Insertion	O (n)	O (n)
Deletion	O (n)	O (n)

The worst case space complexity of an array is O (n).

What Are the Different Array Types?

Arrays can be divided into two categories:

• Arrays in One Dimension:   

A 1d array may be thought of as a row with elements stored one after the other.

• Arrays with Multiple Dimensions:

There are two types of multi-dimensional arrays. They are as follows:

• Arrays in Two Dimensions:

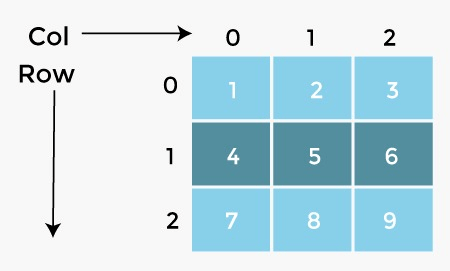
You may think of it as a table with items in each cell.

• Arrays in Three Dimensions:

You may think of it as a cuboid built up of smaller cuboids, each of which can hold an element.

The size of the array

In the C programming language, an array has a fixed size, which means that once the size is set, it cannot be modified, i.e. it cannot be shrunk or expanded. The rationale for this was because while expanding, we can't always be sure (it's not always feasible) that we'll obtain the following memory address as free. The shrinking won't work since the array is RAM statically allocated when it's defined, and the compiler is the only one who can remove it.

In Arrays, there are several types of indexing.

• 0 (Zero Based Indexing) - The array's initial member corresponds to index 0.
• 1 (One Based Indexing) - The array's first member corresponds to index 1.
• n (n Based Indexing) – An array's base index can be customised to meet specific needs.

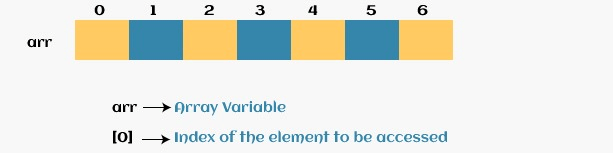
Getting to an Array's Elements –

The following information is required to access any element of an array:

• The array's starting address.
• In bytes, the size of an element.
• Array is the type of indexing that follows.

The following formula may be used to compute the address of any element in a 1D array:

A[i] = base address + size * (i – first index)

Array to Function Passing –

As previously stated, the address of the array's first element is represented by the array's name. The base address may be used to traverse the items of an array.

The following example shows how to provide an array to a function.

The programme below defines the total function, which takes an array as an input. This function computes the sum of all the array's items.

#include<stdio.h>
int total(int[]);
void main()
{
    int array[5] = {0,1,2,3,4};
    int sum = total(array);
    printf(“%d”,sum);
}
int total(int array[])
{
    int sum=0;
    int index;
    for(index=0; index<5; index++)
    {
        sum = sum + array[index];
    }
    return sum;
}

Defined 2D Array

An array of arrays is a common definition for a two-dimensional array. A matrix is another name for a two-dimensional array. A matrix looks like a table with rows and columns’.

Array's Benefits -

• Arrays use a single identifier to represent numerous data components of the same kind.
• Using the index number to retrieve or find an element in an array is simple.
• The index of an array may be simply incremented by one to traverse it.
• For all of its data items, arrays reserve memory in contiguous memory regions.
• Memory overflow is avoided by using arrays.
• There is no extra memory loss because the array memory is present.
• 2D arrays are a good way to display tabular data.

Arrays have certain drawbacks.

Disadvantages of utilising arrays include the inability to adjust the size of the array after it has been declared due to static memory allocation. Here because the pieces are stored in successive memory regions, insertions and deletions are complex, and the shifting operation is also expensive.

Array-based applications.

• Data elements of the same data type are stored in an array.
• It's used to solve matrices problems.
• In a computer, it's used as a lookup table.
• Arrays are also used to implement database records.
• Assists with the implementation of the sorting algorithm.
• Variables of the same type can be stored under the same name.
• CPU scheduling may be done with arrays.
• Stacks, Queues, Heaps, Hash tables, and other data structures are implemented using this class.