FIFO approach
FIFO is first in first out approach.
It is done for the list of elements in data structures where first element will be deleted after another element ia added to it
Here, we treat the information components with a fair opportunity; the component which has entered first will get the chance to leave first.
The other name we call First Come First Serve is executed utilizing the information structure named a line.
The best guide to comprehend the FIFO rule is the point at which we stand in a line and need to take a film ticket, and there are a many individuals remaining before us, and we have no other decision left as opposed to hanging tight for our opportunity.
In the event that we notice the above model, we can undoubtedly see that we will find the opportunity after individuals remaining before us and will be treated as the early bird gets the worm.
The FIFO standard has extraordinary significance in the different cycles booking calculation, which the working framework does to settle the timetable of a few cycles in a steady progression.
One of the calculations that CPU utilizes is FCFS, the early bird gets the worm to allow a fair opportunity to each cycle, and it is executed by utilizing the line information structure.
In one of the crude calculations of booking, we will utilize the cooperative calculation, and the roundabout line has its extraordinary significance; by utilizing the roundabout line, we will actually want to seize the cycle and allow a fair opportunity to each interaction utilizing a round line.
This calculation is utilized by cycle and organization schedulers in processing.
It is likewise utilized in PC controlled Traffic Signal Systems.
It is additionally utilized in CPU planning and memory the executives
The information structure, in view of the FIFO rule, is the line.
In the line information structure, we will play out the two fundamental tasks: first, Enqueue activity for embedding the information components into the line, and one more is Dequeue activity for eliminating the information components from the line.
In stack, we will chiefly utilize two tasks drive for driving the information components into the stack, and another is pop for eliminating the components from the stack.
The line contains two finishes, i.e., the front, and another is the back
Many projects depend on the idea of the FIFO rule.
A line is one of the significant direct information structures widely utilized in different PC applications, and furthermore it depends on the FIFO ( First In First Out ) standard.
It follows a specific request of information execution for which tasks are performed. In this information structure, information enters from one end, i.e., the REAR end, and the following information enters the line after the past one.
Erasure activity is performed from another end, i.e., FRONT
As contrasted and stacks, stacks are likewise a direct information structure.
In spite of the fact that, it depends on LIFO (Last In First Out) rule, which suggests that information enters individually from one end into the stack till it arrives at its end breaking point, and it jumped out the information component from the stack from that end itself.
In a stack, just a single pointer is required for playing out all tasks, which is top, while, in the line, there are two pointers required, back and front, for playing out all activities.
The methodology, as referenced prior, is known as the First-In-First-Out approach or FIFO.
Application of FIFO approach:
The line is a straight information structure in light of the FIFO approach, in which information components go into the line utilizing the backside, and from the front end, cancellation of components happens.
FIFO approach is for the most part utilized in network scaffolds, switches, and switches.
It is additionally sorted as straight line
1. Linear Queue:
A straight line is a direct information structure in light of FIFO (First in First Out) rule, in which information enters from the backside and is erased from the front end.
A direct line is supposed to be the basic line, and at whatever point we want to discuss the line, it is of course set that we are thinking about a straight line.
We will talk about these finishes in more detail further.
Different models like:
Individuals are hanging tight for the transport.
The main individual remaining in the line will be quick to get on the transport.
Vehicles lined at a cost span. The main vehicle to arrive at the scaffold will be quick to leave.
Operations of Linear Queue:
There are sure essential activities has acted in the straight line are as per the following >
Enqueue
For the expansion of information components in the line, this activity is utilized.
By applying this activity, information is placed in the line as per the grouping after each other. Enqueue will be gone on till the line arrives at its end limit.
After it arrives at the endpoint, the information can't add to the line, and afterward such condition is supposed to be an Overflow condition.
En-line activity is finished from the backside.
Dequeue
This activity is utilized to erase an information component from the line.
Utilizing Dequeue activity, that information component is erased, which is enqueued first in the line, or the components are popped in similar request in which they are pushed.
This cycle will erase the information components from the line until the entire line becomes unfilled.
When every one of the components are erased, then the erasure activity can't execute, and afterward such condition is supposed to be an Underflow condition.
It is finished from the front end.
Peek
This activity is utilized to figure out the absolute first line component, which is to be served first without dequeuing it.
Two ends of linear queue:
Front end - It alludes to the underlying or beginning place of the line. The front end is primarily used to erase the information component from the line or play out a dequeue activity.
Rear end - alludes to the last or back position of the line. The backside is predominantly used to embed the line information components or play out the en-line activity.
Methods of implementation linear queue:
1. using array
2. using stack
3. using linked list
Implementation of linear queue:
At first, we really want to make a variety of size 'n' whether statically or powerfully, contingent upon the client.
Announce two pointers named FRONT and REAR.
Introduce REAR = - 1 and FRONT = 0.
Make three capabilities named Enqueue for adding information components in the Queue,
Dequeue for cancellation of an information component from the line, and look for figuring out the principal component from the line without dequeuing it.
//C program code
#include<stdio.h>
#include<stdlib.h>
#define MAX 10
int queue [ MAX ] ; //Declaration of Array
int front = -1 , rear = -1 ;
void enqueue () ;
int dequeue () ;
int peek () ;
void display () ;
void main()
{
int choice , data ;
while ( 1 )
{
printf ( " \n \n ***************** Main ******************** \n " ) ;
printf ( " 1. Inserting the element \n " ) ;
printf ( " 2. Deleting the element \n " ) ;
printf ( " 3. Peek value in the queue \n " ) ;
printf ( " 4. Display the Queue \n " ) ;
printf ( " 5. Exit from queue \n " ) ;
printf ( " Enter your choice of operation : " ) ;
scanf ( "%d" , &choice ) ;
switch ( choice )
{
case 1 :
enqueue () ;
break ;
case 2 :
data = dequeue () ;
if ( data != -1 )
printf ( " \n The data element popped out from queue is -> %d " , data ) ;
break ;
case 3 :
data = peek () ;
if ( data != -1 )
printf ( " \n The first value in queue is -> %d " , data ) ;
break ;
case 4 :
display () ;
break ;
case 5 :
exit ( 0 ) ;
break ;
default :
printf ( " \n Choice not available \n " ) ;
}
}
}
void enqueue ()
{
int val ;
printf ( " Enter data to insert in queue -> " ) ;
scanf ( "%d" , &val ) ;
if ( rear == MAX - 1 )
{
printf ( " Overflow Condition " ) ;
}
else
{
if ( front == -1 )
{
front = 0 ;
}
rear = rear + 1 ;
queue [ rear ] = val ;
}
}
int dequeue ()
{
int val ;
if ( front == -1 || rear < front )
{
printf ( " \n Underflow condition " ) ;
return -1 ;
}
else
{
val = queue [ front ] ;
front = front + 1 ;
if ( front > rear )
{
front = rear = -1 ;
}
return val ;
}
}
int peek ()
{
if ( front == -1 || rear < front )
{
printf ( " \n Queue is empty " ) ;
return -1 ;
}
else
{
return queue [ front ] ;
}
}
void display()
{
int i ;
printf ( " \n " ) ;
if ( front == -1 || front > rear )
{
printf ( " \n Queue is empty " ) ;
}
else
{
for ( i = front ; i <= rear ; i++ )
{
printf ( " %d \n " , queue [ i ] ) ;
}
}
}
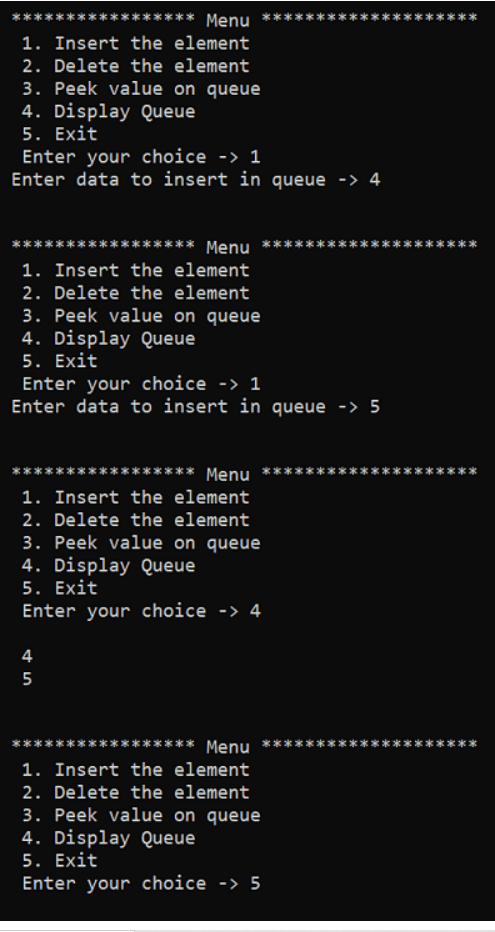
Output: