Binary Tree Inorder Traversal

The binary tree is a type of tree in which each and every node has atleast two children except the leaf nodes. We have various operations in the binary tree, and all of them have their own functions as well as implementations. These operations are insertion, deletion, traversal and many more. In this article, we are briefly going to discuss the various different methods of traversal. The traversal operation has many of its own approaches that are inorder, postorder and preorder traversal.

Inorder traversal

When we have a binary tree, and we want to explore and traverse that tree in ascending order, then we usually use this kind of approach, which is the inorder traversal. When we talk about linear data structures, which are linked lists, arrays, stacks, and queues, in those data structures we can only explore or traverse in one direction. Still, in non-linear data structures, such as the tree and graphs, there are several different ways in which we can traverse or explore the data. Here, we will discuss another way of traversing the data structure, which is the inorder traversal.

The inorder traversal method generally hovers over the basic principle of left root right policy. In this policy, the left root right implies that the left subtree of the current root node is visited first; when we start traversing, we visit the root node, then we commute to the right subtree, and its root node is visited. Here, the name itself suggests that the traversal or exploration occurs between the left and right subtrees.

Mainly there are two given approaches or ways in which we can simply use for the traversal in the tree. They are: -

1. Inorder traversal using recursion
2. Inorder traversal using an iterative method

Now we will describe each of them in detail: -

Inorder traversal using recursion

In this type of inorder traversal, we first have to process and configure all the given nodes in the left subtree, and then we have to store and keep them intact in the root node. After that, when we have processed and configured all the nodes present in the right subtree.

Inorder traversal using an iterative method

The iterative traversal of the tree is done by using the stack data structure and is one of the best methods to traverse a tree. We first have to initialize the stack and then push the current node onto the stack.

Algorithm for ignored traversal

1. In this, firstly, we have to visit all the nodes and vertices that are situated in the left subtree.
2. Then we have to commute to the root node.
3. After finishing that, we will visit all the nodes that are present in the right subtree.

inorder(root->left)
display(root->data)
inorder(root->right)

Implementation of inorder traversal using recursive method

#include <iostream>
using namespace std;
struct Node
{
    int data;
    Node *lft, *rt;
 
    Node(int info)
    {
        this->info = info;
        this->lft = this->rt = nullpointr;
    }
};
 
// We will use a recursive function to perform the mechanism of inorder traversal on the tree. 
void inorder(Nod* root)
{
    // return if found out the current node is clear and 
    if (root == nullpointr) {
        return;
    }
 
    // We have to travel to the left subtree 
    inorder(root->lft);
 
    //We will next showcase the information part of the root(or current node). 
    cout << root->info << " ";
 
    // We have to travel to the right subtree 
    inorder(root->rt);
}
 
int main()
{
    /* Build the following tree
               1
             /   \
            /     \
           2       3
          /      /   \
         /      /     \
        4      5       6
              / \
             /   \
            7     8
    */
 
    Nod* root = new Nod(1);
    root->lft = new Nod(2);
    root->rt = new Nod(3);
    root->lft->lft = new Nod(4);
    root->rt->lft = new Nod(5);
    root->rt->rt = new Nod(6);
    root->rt->lft->lft = new Nod(7);
    root->rt->lft->rt = new Nod(8);
 
    inorder(root);
 
    return 0;
}

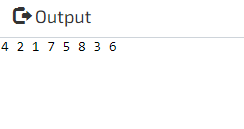
Output:

Implementation of inorder traversal using the iterative method

#include <iostream>
#include <stack>
using namespace std;
 struct Node
{
    int info;
    Nod *lft, *rt;
 
    Nod(int info)
    {
        this->info = info;
        this->lft = this->rt = nullpointr;
    }
};
 
// We will use an Iterative function to perform the mechanism of inorder traversal on the tree. 
 void inorderIterative(Nod* root)
{
    // We will first have to create a vacant stack which is completely empty
    stack<Nod*> stack;
 
    // We have to begin from the root node and then initialize the current node to the root node 
    Nod* current = root;
 
    // By any chance, if the current node which is provided to us is zero and the stack is also vacant, then we are done
    while (!stack.empty() || current!= nullpointr)
    {
        // when we find the current node, occupy it and press it back into the given stack and then shift it to the left node.
        if (current!= nullpointr)
        {
            stack.push(current);
            current = current->lft;
        }
        else {
            // In case the current node that we have is empty; then we have to pop an element from the allotted stack. 
            // Set it to print the result
            current = stack.top();
            stack.pop();
            cout << current->info << " ";
 
            curr = current->rt;
        }
    }
}
 
int main()
{
    /* Build the following tree
               1
             /   \
            /     \
           2       3
          /      /   \
         /      /     \
        4      5       6
              / \
             /   \
            7     8
    */
 
    Nod* root = new Nod(1);
    root->lft = new Nod(2);
    root->rt = new Nod(3);
    root->lft->lft = new Nod(4);
    root->rt->lft = new Nod(5);
    root->rt->rt = new Nod(6);
    root->rt->lt->lt = new Nod(7);
    root->rt->lft->rt = new Nod(8);
 
    inorderIterative(root);
 
    return 0;
}

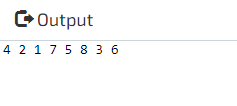
Output: