Create a Complete Binary Tree from its Linked List

Introduction

A binary tree is a data structure that allows us to store a set of elements, called nodes. It stores elements in such a way that it is convenient for retrieving. A binary tree comprises two parts: the tree root node and the left and right subtrees of the tree. The left sub-tree is the leftmost child of the root node, and the right subtree is the rightmost child of the root node.

A linked list is a data structure consisting of a group of nodes that together represent a sequence. Linked lists are often used to implement queues, stacks, and other dynamic data structures. A complete binary tree is a binary tree in which every level of the tree is fully filled, except for perhaps the last level. A complete binary tree is very efficient at both insertion and deletion. It is possible to create a complete binary tree from a linked list. The algorithm is simple and easy to implement. Given a linked list, we can create a complete binary tree by inserting the nodes of the linked list into the tree in level order. The first node in the linked list will be the root of the tree, and subsequent nodes will be inserted into the leftmost available position at each level. This process continues until all nodes of the linked list have been inserted into the tree. The result will be a complete binary tree with the same data as the original linked list.

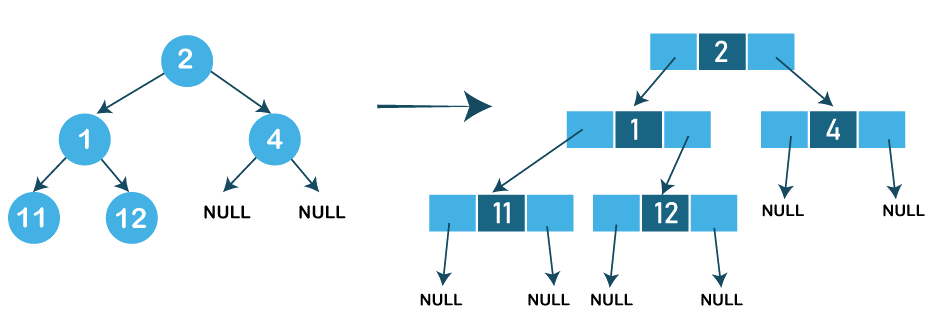
A linked list is a sequence of elements in which each element stores the location of its successor. On the other hand, a binary tree is an abstract data structure that stores items in hierarchical order. Binary trees have long been used for the storage and access of data efficiently and quickly. In this article, we will look at how to create a complete binary tree from a given linked list. We will discuss the step-by-step process of constructing a binary tree while considering time and space complexities.

A binary tree is an alternative representation of a list or a set. It is also referred to as a rooted tree or data structure, and it's the most common representation of numbers in binary form. A binary tree is a data structure that has only two distinct parts: the nodes and the links. A node has two components: a data component and a child component. Each component has its own value, which is the value of the item it contains. In this way, a binary tree is very similar to a linked list.

A linked list is a linear arrangement of elements with each element linked to the next link by a pointer. Essentially, each node contains an array where each element represents the data and child components of the node. To navigate through a binary tree, you only need to know the left and right links. For example, to navigate through binary tree #01 in the form of a linked list, you only need to know the left links- left link #01 and left link #02. To navigate through binary tree #02 in the form of a linked list, you only need to know the right links- right link #01 and right link #02.

A binary tree is a structure that can easily be represented in the form of a tree or a linked list. When storing data in binary form, it's best to use binary trees because they're quick and efficient when storing large amounts of data. Each node in a binary tree has two components: data and child components. The data component stores your original information while the child components allow you to organize your information into different structures such as lists and trees. To create a binary tree, start with an empty directory (node) with two components: data and child components. Then link each component to another component using pointers (links). In this way, you have created your binary tree; now all you have to do is fill it with information!

It's possible to efficiently navigate binary trees using only left and right links- no extra work is required.

How to navigate Binary Tree?

To navigate through binary trees using only left and right links, follow these steps:

• Start at the root directory (node 0),
• then move leftward through each node one link at a time until you reach the end of the linked list (node 2).
• After reaching node 2, return back one step along your left link until you reach the parent node 1).
• From there, move rightward through each child node until you reach your desired item;
  • there are no child nodes, return back one step along your parent node until reaching your desired item.

A binary tree is an efficient way to store large amounts of data efficiently because it uses less space than other storage methods such as arrays or lists. It's also easy to navigate through because you need only know your left and right links- no extra work is required.

Complete Binary Tree from its Linked List

Assuming we have a linked list where each node has a value and pointer to the next node in the list:

To create a complete binary tree from this linked list, we can do a breadth-first traversal of the list, i.e.,

• starting from the head of the list, we visit each node in order and add it to the tree.
• For each node in the list, we add its left child by traversing to the node with the next lower value.
• If there is no such node, we add a null child.
• We then add its right child by traversing to the node with the next higher value. If there is no such node, we again add a null child.
• We continue this process until we reach the end of the linked list. The resulting tree will be a complete binary tree with all levels filled except for possibly the last level which will be filled from left to right.

C++ Code for representation of binary tree in linked list

#include <bits/stdc++.h>
using namespace std;
//the  Link list Node
struct LL_Node
{
    int data;
    struct LL_Node *next;
    LL_Node(int x)
    {
        data = x;
        next = NULL;
    }
};
// Tree Node
struct Tree_Node
{
    int data;
    Tree_Node *left;
    Tree_Node *right;
    Tree_Node(int x)
    {
        data = x;
        left = NULL;
        right = NULL;
    }
};
// Inserting nodes at the beginning of the Linked List
void push_to_LL(struct LL_Node **head, int new_data)
{
    struct LL_Node *new_node = new LL_Node(new_data);
    new_node->next = *head;
    *head = new_node;
}
// To perform inorder traversal of the created tree
void inorder_traversal(Tree_Node *root)
{
    if (root)
    {
        inorder_traversal(root->left);
        cout << root->data << " ";
        inorder_traversal(root->right);
    }
}
// To reverse Linked List
void reverse_LL(LL_Node **head)
{
    LL_Node *prev = NULL;
    LL_Node *cur = *head;
    LL_Node *nxt;
    while (cur != NULL)
    {
        nxt = cur->next;
        cur->next = prev;
        prev = cur;
        cur = nxt;
    }
    *head = prev;
}
// To convert the Linked List to Binary Tree
void convert_LL_to_BinaryTree(LL_Node *head, Tree_Node *&root)
{
    if (head == NULL)
        return;
    // create an empty queue
    queue<Tree_Node *> q;
    LL_Node *curr = head;
    // create root of the tree
    root = new Tree_Node(curr->data);
    q.push(root);
    // until the linked list is empty, run the while loop
    while (curr->next != NULL)
    {
        Tree_Node *temp = q.front();
        if (curr->next != NULL)
        {
            curr = curr->next;
            // insert left child of tree
            temp->left = new Tree_Node(curr->data);
            // add it in the queue
            q.push(temp->left);
        }
        if (curr->next != NULL)
        {
            curr = curr->next;
            // insert right child of tree
            temp->right = new Tree_Node(curr->data);
            // add it in the queue
            q.push(temp->right);
        }
        //remove the parent node from the queue
        q.pop();
    }
}
int main()
{
    struct LL_Node *head = NULL;
    push_to_LL(&head, 1);
    push_to_LL(&head, 2);
    push_to_LL(&head, 3);
    push_to_LL(&head, 4);
    push_to_LL(&head, 5);
    push_to_LL(&head, 6);
    // reverse the Linked List
    reverse_LL(&head);
    Tree_Node *root = NULL;
    // construct the Binary Tree
    cout<<"The inorder traversal of the binary tree is:"<<endl;
    convert_LL_to_BinaryTree(head, root);
    inorder_traversal(root);
    return 0;
}

Example to Create a Complete Binary Tree from its Linked List

Given a Linked List, create a Complete Binary Tree. The idea is to first find the middle node of the linked list and make it the root of the tree. We then recursively do the same for the left and right halves. The algorithm has mainly two steps.

1) Get the middle of the linked list and make it the root of the tree.

2) Recursively we do the same for the left half and right half.

a) Also get the middle of the left half and make it the left child of the root created in step 1.

b) Now get the middle of the right half and make it the right child of the root created in step 1.

/* Function to get to the middle of the linked list */

void _getMiddle(struct Node *head, struct Node **middle){
struct Node *slow_ptr = head;
struct Node *fast_ptr = head;
if (head==NULL){
*middle = NULL;
return;
}
while (fast_ptr != NULL && fast_ptr->next != NULL){
fast_ptr = fast_ptr->next->next; // move to next element in linked list
/* we need the reference to the previous element as we are changing slow pointer */
slow_prev = slow_ptr; // keep track of the  previous node also
slow_ptr = slow_ptr->next; 

Complete Binary Tree from its Linked List

Assuming we have a linked list of N nodes, we can create a complete binary tree with those nodes in O(N) time. The idea is to insert nodes in level order. We first set the root as the first node of the linked list. Then we insert the remaining nodes into the tree. To insert a node at its correct position, we traverse all levels one by one starting from the root. For every level, we compare the leftmost child with the node to be inserted. If the node to be inserted is less than the leftmost child, then we insert it as a left child of that level’s root. Otherwise, we traverse to the right child and continue this process until we find an empty slot.

We can also use a queue for the process of insertion. Start by enqueuing the root node. Then for each level, while there are still nodes in the queue:

- Dequeue a node from the queue and make it the left child of the current node

- If there are more nodes in the queue:

- Dequeue another node from the queue and make it the right child of the current node

- Enqueue the current node's left and right children (if they exist)

Conclusion

A complete binary tree is a type of binary tree in which every level of the tree is fully filled, except for possibly the last level. A complete binary tree is very useful for certain algorithms, such as heap sort, but constructing one from a linked list can be tricky.