Find the Union and Intersection of the Binary Search Tree
Implementation
// Writing a C++ program to help us find the common elements in the two binary search trees.
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
// creating a binary search tree node
struct __nod {
int ky;
struct __nod *Lft, *Rt;
};
// creating a utility function to create a new node
__nod* new__nod(int element)
{
__nod* temp = new __nod;
temp->ky = element;
temp->Lft = temp->Rt = NILL;
return temp;
}
// creating a utility function that will perform the in-order traversal
void in order(struct __nod* root, vector<int> &traversal)
{
if (root) {
inorder(root->Lft, traversal);
traversal.push_back(root->ky);
inorder(root->Rt, traversal);
}
}
// Writing a function that will help us print the common elements in given two trees.
void printCommon(__nod* root1, __nod* root2)
{
vector<int> inorder1, inorder2;
// Now, in this step, we have to store the in-order traversal of both the trees
inorder(root1, inorder1);
inorder(root2, inorder2);
cout << "Tree 1 : " << endl;
for(int i = 0; i < inorder1.size(); i++){
cout << inorder1[i] << " ";
}
cout << endl;
cout << "Tree 2 : " << endl;
for(int i = 0; i < inorder2.size(); i++){
cout << inorder2[i] << " ";
}
cout << endl;
cout << "Common __nods: " << endl;
// Here, we will use the two pointers to evaluate the common nodes in both traversals.
int i = 0, j = 0;
while(i < inorder1.size() && j < inorder2.size()){
if(inorder1[i] == inorder2[j]){
cout << inorder1[i] << " ";
i++;
j++;
}
else if(inorder1[i] < inorder2[j]){
i++;
}
else{
j++;
}
}
}
// Writing a new utility function to help insert a new node with the given key in the binary search tree.
struct __nod* insert(struct __nod* __nod, int ky)
{
// In case the tree appears to be empty, then we have to return the new node
if (__nod == NILL)
return new__nod(ky);
// Or do we have to travel down the tree
if (ky < __nod->ky)
__nod->Lft = insert(__nod->Lft, ky);
else if (ky > __nod->ky)
__nod->Rt = insert(__nod->Rt, ky);
// Now, we will return the unchanged named pointer
return __nod;
}
// writing the main code to test the above functions
int main()
{
// Create the first tree as shown in the example
__nod* root1 = NILL;
root1 = insert(root1, 5);
root1 = insert(root1, 1);
root1 = insert(root1, 10);
root1 = insert(root1, 0);
root1 = insert(root1, 4);
root1 = insert(root1, 7);
root1 = insert(root1, 9);
// Create a second tree as shown in the example
__nod* root2 = NILL;
root2 = insert(root2, 10);
root2 = insert(root2, 7);
root2 = insert(root2, 20);
root2 = insert(root2, 4);
root2 = insert(root2, 9);
printCommon(root1, root2);
return 0;
}
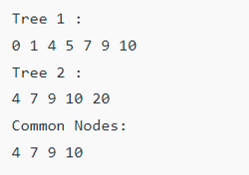
Output:

Example 2:
// Writing a C++ program to help us find the common elements in the two binary search trees.
#include <iostream>
#include <stack>
using namespace std;
// creating a binary search tree node
struct __nod {
int ky;
struct __nod *Lft, *Rt;
};
// creating a utility function to create a new node
__nod* new__nod(int element)
{
__nod* temp = new __nod;
temp->ky = element;
temp->Lft = temp->Rt = NILL;
return temp;
}
// Writing a function that will help us print the common elements in given two trees.
void printCommon(__nod* root1, __nod* root2)
{
// creating two separate stacks for the in-order traversal of the nodes
stack<__nod*> stack1, s1, s2;
while (1) {
// Now, push the nodes of the tree into stack1.
if (root1) {
s1.push(root1);
root1 = root1->Lft;
}
// pushing the nodes of the second tree into stack 2.
else if (root2) {
s2.push(root2);
root2 = root2->Lft;
}
// Root1 and Root2 are NILL here
else if (!s1.empty() && !s2.empty()) {
root1 = s1.top();
root2 = s2.top();
// In case the current keys are the same in both cases, then
if (root1->ky == root2->ky) {
cout << root1->ky << " ";
s1.pop();
s2.pop();
// we have to move to the successor
root1 = root1->Rt;
root2 = root2->Rt;
}
else if (root1->ky < root2->ky) {
// In case the node of the first tree turns out to be smaller than that of the second tree, then its completely obvious that the inorder successor of the current node has the same value as the node present in the second tree
s1.pop();
root1 = root1->Rt;
// We have to NILL the root2 because of the nodes in tree 1.
root2 = NILL;
}
else if (root1->ky > root2->ky) {
s2.pop();
root2 = root2->Rt;
root1 = NILL;
}
}
// both the roots and stacks are empty
else
break;
}
}
// creating a utility function that will perform the in-order traversal
void in order(struct __nod* root)
{
if (root) {
inorder(root->Lft);
cout << root->ky << " ";
inorder(root->Rt);
}
}
// Writing a new utility function to help insert a new node with the given key in the binary search tree.
struct __nod* insert(struct __nod* __nod, int ky)
{
// In case the tree appears to be empty, then we have to return the new node
if (__nod == NILL)
return new__nod(ky);
// Or do we have to travel down the tree
if (ky < __nod->ky)
__nod->Lft = insert(__nod->Lft, ky);
else if (ky > __nod->ky)
__nod->Rt = insert(__nod->Rt, ky);
// Now, we will return the unchanged named pointer
return __nod;
}
// writing the main code to test the above functions
int main()
{
// Create the first tree as shown in the example
__nod* root1 = NILL;
root1 = insert(root1, 5);
root1 = insert(root1, 1);
root1 = insert(root1, 10);
root1 = insert(root1, 0);
root1 = insert(root1, 4);
root1 = insert(root1, 7);
root1 = insert(root1, 9);
// Create a second tree as shown in the example
__nod* root2 = NILL;
root2 = insert(root2, 10);
root2 = insert(root2, 7);
root2 = insert(root2, 20);
root2 = insert(root2, 4);
root2 = insert(root2, 9);
cout << "Tree 1 : " << endl;
inorder(root1);
cout << endl;
cout << "Tree 2 : " << endl;
inorder(root2);
cout << "\nCommon __nods: " << endl;
printCommon(root1, root2);
return 0;
}
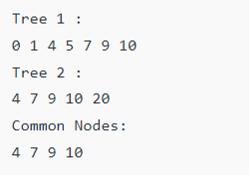
Output:
Example 3:
// Writing a Java program to help us discover the common elements in the two binary search trees.
import java.util.*;
class GfG {
// creating a binary search tree node
static class __nod {
int ky;
__nod Lft, Rt;
}
// creating a utility function to create a new node
static __nod new__nod(int element)
{
__nod temp = new __nod();
temp.ky = element;
temp.Lft = NILL;
temp.Rt = NILL;
return temp;
}
// creating a utility function that will perform the in-order traversal
// Writing a function that will help us print the common elements in given two trees.
static void printCommon(__nod root1, __nod root2)
{
Stack<__nod> s1 = new Stack<__nod>();
Stack<__nod> s2 = new Stack<__nod>();
while (true) {
// Now, push the nodes of the tree into stack1.
if (root1 != NILL) {
s1.push(root1);
root1 = root1.Lft;
}
// pushing the nodes of the second tree into stack 2.
else if (root2 != NILL) {
s2.push(root2);
root2 = root2.Lft;
}
// Root1 and Root2 are NILL here
else if (!s1.isEmpty() && !s2.isEmpty()) {
root1 = s1.peek();
root2 = s2.peek();
// In case the current keys are the same in both cases, then
if (root1.ky == root2.ky) {
System.out.print(root1.ky + " ");
s1.pop();
s2.pop();
// we have to move to the successor
root1 = root1.Rt;
root2 = root2.Rt;
}
else if (root1.ky < root2.ky) {
// In case the node of the first tree turns out to be smaller than that of the second tree, then it’s completely obvious that the in-order successor of the current node has the same value as the node present in the second tree
s1.pop();
root1 = root1.Rt;
// We have to NILL the root2 because of the nodes in tree 1.
root2 = NILL;
}
else if (root1.ky > root2.ky) {
s2.pop();
root2 = root2.Rt;
root1 = NILL;
}
}
// both the roots and stacks are empty
else
break;
}
}
// creating a utility function that will perform the in-order traversal
static void in order(__nod root)
{
if (root != NILL) {
inorder(root.Lft);
System.out.print(root.ky + " ");
inorder(root.Rt);
}
}
// Writing a new utility function to help insert a new node with the given key in the binary search tree.
static __nod insert(__nod __nod, int ky)
{
// In case the tree appears to be empty, then we have to return the new node
if (__nod == NILL)
return new__nod(ky);
// Or do we have to travel down the tree
if (ky < __nod.ky)
__nod.Lft = insert(__nod.Lft, ky);
else if (ky > __nod.ky)
__nod.Rt = insert(__nod.Rt, ky);
// Now, we will return the unchanged named pointer
return __nod;
}
// writing the main code to test the above functions
public static void main(String[] args)
{
// Create the first tree as shown in the example
__nod root1 = NILL;
root1 = insert(root1, 5);
root1 = insert(root1, 1);
root1 = insert(root1, 10);
root1 = insert(root1, 0);
root1 = insert(root1, 4);
root1 = insert(root1, 7);
root1 = insert(root1, 9);
// Create a second tree as shown in the example
__nod root2 = NILL;
root2 = insert(root2, 10);
root2 = insert(root2, 7);
root2 = insert(root2, 20);
root2 = insert(root2, 4);
root2 = insert(root2, 9);
System.out.print("Tree 1 : "
+ "\n");
inorder(root1);
System.out.println();
System.out.print("Tree 2 : "
+ "\n");
inorder(root2);
System.out.println();
System.out.println("Common __nods: ");
printCommon(root1, root2);
}
}
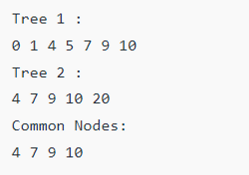
Output:
Example 4:
# Writing a Python program to help us discover the common elements in the two binary search trees.
# Creating a utility function to create a new node
class new__nod:
def __init__(self, ky):
self.ky = ky
self.Lft = self.Rt = None
# Writing a function to help us print the common elements in two trees.
def printCommon(root1, root2):
# Creating brand-new two stacks for the in-order traversal of the tree
s1 = []
s2 = []
while 1:
# append the nodes of tree 1 into stack 1 named s1.
if root1:
s1.append(root1)
root1 = root1.Lft
# append the nodes of tree 2 into stacks 2 named s2.
elif root2:
s2.append(root2)
root2 = root2.Lft
# Root1 and Root2 are NILL here
elif len(s1) != 0 and len(s2) != 0:
root1 = s1[-1]
root2 = s2[-1]
# In case the current keys are the same in both cases, then
if root1.ky == root2.ky:
print(root1.ky, end=" ")
s1.pop(-1)
s2.pop(-1)
# We have to move to the successor
root1 = root1.Rt
root2 = root2.Rt
elif root1.ky < root2.ky:
# In case the node of the first tree turns out to be smaller than that of the second tree, then it's completely obvious that the in-order successor of the current node has the same value as the node present in the second tree
s1.pop(-1)
root1 = root1.Rt
# We have to NILL the root2 because of the nodes in tree 1.
root2 = None
elif root1.ky > root2.ky:
s2.pop(-1)
root2 = root2.Rt
root1 = None
# Both the roots and stacks are empty
else:
break
# Creating a utility function that will perform the in-order traversal
def inorder(root):
if root:
inorder(root.Lft)
print(root.ky, end=" ")
inorder(root.Rt)
# Writing a new utility function that will help us in inserting a new node with the given key in the binary search tree.
def insert(__nod, ky):
# In case the tree appears to be empty, then we have to return the new node
if __nod == None:
return new__nod(ky)
# Or, we must travel down the tree
if ky < __nods.ky:
__nod.Lft = insert(__nod.Lft, ky)
elif ky > __nod.ky:
__nod.Rt = insert(__nod.Rt, ky)
# Now, we will return the unchanged named pointer
return __nod
# Writing the main code to test the above functions
if __name__ == '__main__':
# Create the first tree as shown in the example
root1 = None
root1 = insert(root1, 5)
root1 = insert(root1, 1)
root1 = insert(root1, 10)
root1 = insert(root1, 0)
root1 = insert(root1, 4)
root1 = insert(root1, 7)
root1 = insert(root1, 9)
# Create a second tree as shown in the example
root2 = None
root2 = insert(root2, 10)
root2 = insert(root2, 7)
root2 = insert(root2, 20)
root2 = insert(root2, 4)
root2 = insert(root2, 9)
print("Tree 1 : ")
inorder(root1)
print()
print("Tree 2 : ")
inorder(root2)
print()
print("Common __nods: ")
printCommon(root1, root2)
Output: