Recursion - Factorial and Fibonacci

In this article, we will learn how to find the factorial of a number and the Fibonacci series up to n using the recursion method.

What is recursion?

Defining anything in terms of itself is called recursion. Recursion is so powerful tool in the programming language that we used to solve many real-life problems easily. When in the body of a function, if any statement calls the same function or another function then that function is recursive in nature. The properties of recursion include the base criteria and progressive approach. Any recursive function should follow these two essential properties.

The Base criteria or conditions define the condition for the function call to stop, and the progressive approach defines that the result should come close to the base criteria after each function call.

• Factorial – The factorial of a number is defined as the product of all the integers less than it and the number itself. It is determined as n! = n * (n-1)!

Q. Write a C++ program to print the factorial of a number using the recursive method.

// C++ program to find the factorial of a number using recursive method.
#include <iostream>
using namespace std;


// Function to calculate the factorial of a number through recursion.
int factorial(int n)
{
    // Base Criteria
    if (n == 0 || n == 1)
    {
        return 1;
    }


    // Calculating the factorial using the recursive method.
    else
    {
        return n * factorial(n - 1);
    }
}


// Driver Function
int main()
{
    // Variable to store the user inputs
    int x;
    cout << "To exit the program enter a negative number!" << endl;
    while (1) // Always True
    {
        cout << "Enter a number: ";
        cin >> x;


        // The while loop terminates when the user enters a negative integer.
        if (x < 0)
        {
            cout << "Exited Successfully!" << endl;
            break;
        }
        // Calling the factorial function, passing the value, and storing it in the fact variable.
        int fact = factorial(x);


        // Ternary operator
        fact > 0 ? cout << "The factorial of " << x << " is = " << fact << endl : cout << "Enter a positive number!" << endl;
    }


    return 0;
}

The possible output of the above program is given below:

Enter a negative number to exit the program!
Enter a number: 0
The factorial of 0 is = 1
Enter a number: 4
The factorial of 4 is = 24
Enter a number: 5
The factorial of 5 is = 120
Enter a number: 10
The factorial of 10 is = 3628800
Enter a number: -1
Exited Successfully!

As we know, the factorial of zero and one is 1. Hence, in the base criteria of the factorial function, we return 1 if the value of n is 0 or 1. In the else part, we return the product of factorial (n-1) and n itself.

int factorial(int n)
{
    if (n == 0 || n == 1)
    {
        return 1;
    }
    else
    {
        return n * factorial(n - 1);
    }
}

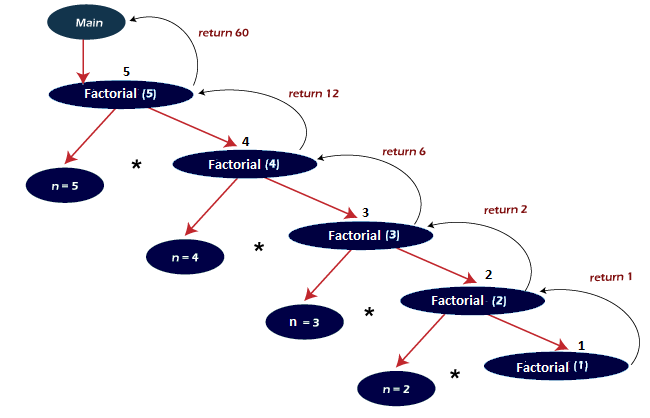
Let us now see the activation record after each function calls and how these recursive functions calls are done:

Operation	Activation Record	Value Return	Remark
Push(main())	main()	-	The main function is called, and we enter n = 5. The main function is pushed into the stack as soon as it calls the factorial function. The control is transferred to the factorial function.
Push(factorial(5))	factorial(5) main()	-	Here, n = 5; hence the base condition is not satisfied, and in the else, it calls itself with n = 4. It is pushed into the stack, and the control is transferred to the factorial function with n = 4.
Push(factorial(4))	factorial(4) factorial(5) main()	-	Here also, the base condition is not satisfied. We push Factorial (4) because it calls itself with the value of n = 3.
Push(factorial(3))	factorial(3) factorial(4) factorial(5) main()	-	We push Factorial (3) because it calls itself with the value of n = 2.
Push(factorial(2))	factorial(2) factorial(3) factorial(4) factorial(5) main()	Factorial (1) = 1	We push Factorial (2) because it also calls itself with the value n = 1. Here, the base condition is satisfied, and factorial (1) returns 1.
Pop(factorial(2))	factorial(3) factorial(4) factorial(5) main()	Factorial (2) = 2	Factorial (2) returns 2 and is popped from the stack. The control is again transferred to factorial(3).
Pop(factorial(3))	factorial(4) factorial(5) main()	Factorial (3) = 6	Factorial (3) returns 6 and is popped from the stack. The control is now transferred to factorial(4).
Pop(factorial(4))	factorial(5) main()	Factorial (4) = 24	Factorial (4) returns 24 and is popped from the stack. The control is now transferred to factorial(5).
Pop(factorial(3))	main()	Factorial (5) = 120	Factorial (5) returns 120 and is popped from the stack. The control is again transferred to the main function.
Pop(main())	NULL	0	The program terminates after the main function returns 0.

The above function calls are shown in the figure below and the numbering associated with them tells us which function call is evaluated first:

• Fibonacci Series – In the Fibonacci series, the nth term is equal to the sum of the previous two terms of the series.

Q. Write a C++ program to print the Fibonacci series up to n terms.

// C++ program to print the Fibonacci series up to n terms.
#include <iostream>
using namespace std;


// Function to find any term of the Fibonacci series.
int fibonacci_series(int n)
{
    // Base Criteria
    if (n == 0 || n == 1)
    {
        return n;
    }


    // Recursive Method
    else
    {
        return fibonacci_series(n - 1) + fibonacci_series(n - 2);
    }
}


// Driver Function
int main()
{
    int n, x;
    cout << "Enter a number: ";
    cin >> n;
    cout << "Fibonacci Series up to n terms: ";


    // Calling the function n times.
    for (int i = 0; i < n; i++)
    {
        x = fibonacci_series(i);
        cout << x << " ";
    }
    return 0;
}

The sample output of the above program is given below:

// Output 1
Enter a number: 5
Fibonacci Series up to n terms: 0 1 1 2 3


// Output 2
Enter a number: 10
Fibonacci Series up to n terms: 0 1 1 2 3 5 8 13 21 34


// Output 3
Enter a number: 15
Fibonacci Series up to n terms: 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377

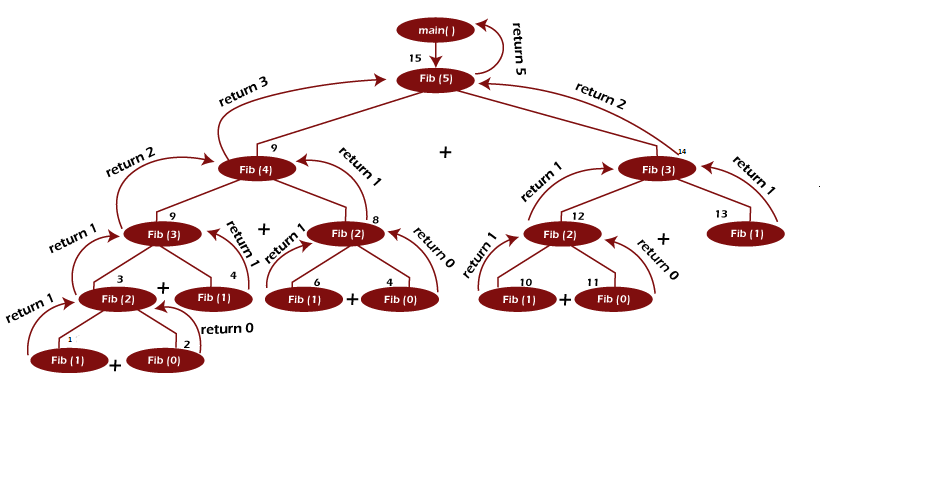
In the above method, we have used recursion to find the Fibonacci series. Let us see how the function calls are done in the above method. Assume that n = 5 is passed to the fibonacci_series function. We have used fib for the Fibonacci function.

Operation	Activation Record	Value Return	Remark
Push(main())	main()	-	The main function calls the Fibonacci function with n = 5. Hence, it is pushed into the stack, and the control is transferred to the Fibonacci function.
Push(fib(5))	fib(5) main()	-	The fib(5) function calls the fib(4) and fib(3) functions. So, we pushed it into the stack. Here, we have two function calls, fib(4) will be evaluated first and then fib(3).
Push(fib(3))	fib(3) fib(5) main()	-	Fib(4) is called itself, so we push fib(3) into the stack and start evaluating fib(4).
Push(fib(4))	fib(4) fib(3) fib(5) main()	-	The fib(4) calls fib(3) and fib(2). So we push fib(4) into the stack.
Push(fib(2)	fib(2) fib(4) fib(3) fib(5) main()	-	Fib(3) is called itself, so we push fib(2) into the stack and start evaluating fib(3).
Push(fib(3))	fib(3) fib(2) fib(4) fib(3) fib(5) main()	-	But fib(3) calls fib(2) and fib(1), so we push fib(3) in the stack. Now, we evaluate fib(2) first and then fib(1).
Push(fib(1))	fib(1) fib(3) fib(2) fib(4) fib(3) fib(5) main()	-	Fib(2) is called itself. So, we push fib(1) into the stack and start evaluating fib(2).
Push(fib(2))	fib(2) fib(1) fib(3) fib(2) fib(4) fib(3) fib(5) main()	-	But fib(2) calls fib(1) and fib(0), so we push fib(2) in the stack.
Push(fib(0))	fib(0) fib(2) fib(1) fib(3) fib(2) fib(4) fib(3) fib(5) main()	Fib(1) = 1	Now, fib(1) will be called itself and we push fib(0) into the stack. Fib(1) returns 1 to its previous call, which is fib(2).
Pop()	fib(2) fib(1) fib(3) fib(2) fib(4) fib(3) fib(5) main()	fib(0) = 0	We pop fib(0) from the stack, which returns 0 to fib(2). Now, evaluate fib(2).
Pop()	fib(1) fib(3) fib(2) fib(4) fib(3) fib(5) main()	fib(2) = 1	We pop fib(2) from the stack. Fib(2) returns 1 sum of fib(1) = 1 and fib(0) = 0 to fib(3). Now, evaluate fib(1).
Pop()	fib(3) fib(2) fib(4) fib(3) fib(5) main()	fib(1) = 1	We pop fib(1) from the stack, which returns 1 to fib(3). Now, evaluate fib(3).
Pop()	fib(2) fib(4) fib(3) fib(5) main()	fib(3) = 2	We pop fib(3) from the stack which returns 2 sum of fib(2) = 1 and fib(1) = 1 to fib(4). Now evaluate fib(2).
Push(fib(0))	fib(0) fib(2) fib(4) fib(3) fib(5) main()	fib(1) = 1	Here, fib(2) calls fib(1) and fib(0). Fib(1) is called itself and we push fib(0) into the stack. On evaluating fib(1) returns 1 to fib(2).
Pop()	fib(2) fib(4) fib(3) fib(5) main()	fib(0) = 0	We pop fib(0) from the stack, which returns 0 to fib(2). Now, evaluate fib(2).
Pop()	fib(4) fib(3) fib(5) main()	fib(2) = 1	We pop fib(2) from the stack which returns 1 sum of fib(1) = 1 and fib(0) = 0 to fib(4). Now, evaluate fib(4).
Pop()	fib(3) fib(5) main()	fib(4) = 3	We pop fib(4) from the stack which returns 3 sum of fib(3) = 2 and fib(2) = 1 to fib(4). Now, evaluate fib(3).
Push(fib(1))	fib(1) fib(3) fib(5) main()	-	Here, fib(3) calls fib(2) and fib(1). Fib(2) is called itself, so we push fib(1) into the stack.
Push(fib(2))	fib(2) fib(1) fib(3) fib(5) main()		Here, fib(2) calls fib(1) and fib(0). So we push fib(2) in the stack.
Push(fib(0))	fib(0) fib(2) fib(1) fib(3) fib(5) main()	fib(1) = 1	Fib(1) is called itself, so we push fib(0) in the stack. Here, fib(1)  returns 1 to fib(2) as per the base condition. Now, evaluate fib(0).
Pop()	fib(2) fib(1) fib(3) fib(5) main()	fib(0) = 0	We pop fib(0) from the stack, which returns 0 to fib(2) as per the base condition. Now evaluate fib(2).
Pop()	fib(1) fib(3) fib(5) main()	fib(2) = 1	We pop fib(2) from the stack. Fib(2) returns 1 sum of fib(1) = 1 and fib(0) = 0 to fib(3). Now, evaluate fib(1).
pop()	fib(3) fib(5) main()	fib(1) = 1	We pop fib(1) from the stack, which returns 1 to fib(3). Now, evaluate fib(3).
Pop()	fib(5) main()	fib(3) = 3	We pop fib(3) from the stack which returns 2 sum of fib(2) = 1 and fib(1) = 1 to fib(5). Now evaluate fib(5).
Pop()	main()	fib(5) = 5	We pop fib(5) from the stack which returns 5 sum of fib(4) = 3 and fib(3) = 2 to the main function. The control now transfers to the main function
Pop()	Empty stack	-	The main function runs other lines of code, and then the program terminates.

The above function call is also shown in the figure given below, and the numbering associative with each function calls tell us which function call is evaluated first.