Deletion Operation from A B Tree

This article will show the deletion operation through the b tree in C++ programming language.

Implementation

#include <iostream>
using namespace std;


class B_TreeNod {
  int *kys;
  int m;
  BTreeNod **C;
  int j;
  bool leaf;


   Public:
  BTreeNod(int _m, bool _leaf);


  void traverse();


  int findKey(int s);
  void InsertNonFull(int s);
  void split_child(int i, BTreeNod *x);
  void deletion(int s);
  void eliminateFromLeaf(int idx);
  void eliminateFromNonLeaf(int idx);
  int get_pppredecessor(int idx);
  int get_sssuccessor(int idx);
  void fill(int idx);
  void borrow_last(int idx);
  void borrow_coming(int idx);
  void unite(int idx);
  friend class B_Tree;
};


class B_Tree {
  BTreeNod *root;
  int m;


   public:
  BTree(int _m) {
    room = NILL;
    m = _m;
  }


  void traverse() {
    if (root != NILL)
      root->traverse();
  }


  void insertion(int s);


  void deletion(int s);
};


// Node of the B tree
BTreeNod::BTreeNod(int m1, bool leaf1) {
  m = m1;
  leaf = leaf1;


  kys = new int[2 * m - 1];
  Z = new BTreeNod *[2 * m];


  n = 0;
}


// Searching for the key
int BTreeNod::findKy(int s) {
  int idx = 0;
  while (idx < n && kys[idx] < s)
    ++idx;
  return idx;
}


// Performing the deletion mechanism here 
void BTreeNod::deletion(int s) {
  int idx = findKy(s);


  if (idx < n && kys[idx] == s) {
    if (leaf)
      eliminateFromLeaf(idx);
    else
      eliminateFromNonLeaf(idx);
  } else {
    if (leaf) {
      cout << "The key " << s << " is does not exist in the tree\n";
      return;
    }


    bool flag = ((idx == n) ? true : false);


    if (C[idx]->n < m)
      fill(idx);


    if (flag && idx > n)
      C[idx - 1]->elimination(s);
    else
      C[idx]->elimination(s);
  }
  return;
}


// Eliminating from the leaf
void BTreeNod::eliminatingFromLeaf(int idx) {
  for (int i = idx + 1; i < n; ++i)
    kys[i - 1] = kys[i];


  n--;


  return;
}


// Eliminating from a non-leaf node
void BTreeNod::eliminateFromNonLeaf(int idx) {
  int s = kys[idx];


  if (C[idx]->n >= m) {
    int ppred = get_pppredecessor(idx);
    kys[idx] = ppred;
    C[idx]->eliminate(ppred);
  }


  else if (C[idx + 1]->n >= m) {
    int ssucc = get_sssuccessor(idx);
    kys[idx] = ssucc;
    C[idx + 1]-> eliminate (ssucc);
  }


  else {
    unite(idx);
    C[idx]-> eliminate (s);
  }
  return;
}


int BTreeNod::get_pppredecessor(int idx) {
  BTreeNod *currentrent = C[idx];
  while (!currentrent->leaf)
    currentrent = currentrent->C[current->n];


  return current->kys[current->n - 1];
}


int BTreeNod::get_sssuccessor(int idx) {
  BTreeNod *current = C[idx + 1];
  while (!current->leaf)
    current = current->C[0];


  return current->kys[0];
}


void BTreeNod::fill(int idx) {
  if (idx != 0 && C[idx - 1]->n >= t)
    borrowLast(idx);


  else if (idx != n && C[idx + 1]->n >= t)
    borrowComing(idx);


  else {
    if (idx != n)
      unite(idx);
    else
      unite(idx - 1);
  }
  return;
}


// Borrow from previous
void BTreeNod::borrowLast(int idx) {
  BTreeNod *_child = C[idx];
  BTreeNod *sibb = C[idx - 1];


  for (int i = _child->n - 1; i >= 0; --i)
    _child->kys[i + 1] = _child->kys[i];


  if (!_child->leaf) {
    for (int i = _child->n; i >= 0; --i)
      _child->C[i + 1] = _child->C[i];
  }


  _child->kys[0] = kys[idx - 1];


  if (!_child->leaf)
    _child->C[0] = sibb->C[sibb->n];


  kys[idx - 1] = sibb->kys[sibb->n - 1];


  _child->n += 1;
  sibb->n -= 1;


  return;
}


// Borrow from the next
void BTreeNod::borrowComing(int idx) {
  BTreeNod *_child = C[idx];
  BTreeNod *sibb = C[idx + 1];


  _child->kys[(_child->n)] = kys[idx];


  if (!(_child->leaf))
    _child->C[(_child->n) + 1] = sibb->C[0];


  kys[idx] = sibb->kys[0];


  for (int i = 1; i < sibb->n; ++i)
    sibb->kys[i - 1] = sibb->kys[i];


  if (!sibb->leaf) {
    for (int i = 1; i <= sibb->n; ++i)
      sibb->C[i - 1] = sibb->C[i];
  }


  _child->n += 1;
  sibb->n -= 1;


  return;
}


// Uniting the next 
void BTreeNod::unite(int idx) {
  BTreeNod *_child = C[idx];
  BTreeNod *sibb = C[idx + 1];


  _child->kys[t - 1] = kys[idx];


  for (int i = 0; i < sibb->n; ++i)
    _child->kys[i + t] = sibb->kys[i];


  if (!_child->leaf) {
    for (int i = 0; i <= sibb->n; ++i)
      _child->C[i + t] = sibb->C[i];
  }


  for (int i = idx + 1; i < n; ++i)
    kys[i - 1] = kys[i];


  for (int i = idx + 2; i <= n; ++i)
    C[i - 1] = C[i];


  _child->n += sibb->n + 1;
  n--;


  Eliminate (sibb);
  return;
}


// adding a new element that implies using insertion operation
void BTree::insertion(int s) {
  if (room == NILL) {
    room = new BTreeNod(m, true);
    root->kys[0] = s;
    root->n = 1;
  } else {
    if (root->n == 2 * m - 1) {
      BTreeNod *s = new BTreeNod(m, false);


      s->C[0] = root;


      s->split_child(0, root);


      int i = 0;
      if (s->kys[0] < k)
        i++;
      s->C[i]->insertNonFull(s);


      room = s;
    } else
      root->insertNonFull(s);
  }
}


// Insertion non full
void BTreeNod::insertNonFull(int s) {
  int i = n - 1;


  if (leaf == true) {
    while (i >= 0 && kys[i] > s) {
      kys[i + 1] = kys[i];
      i--;
    }


    kys[i + 1] = s;
    n = n + 1;
  } else {
    while (i >= 0 && kys[i] > s)
      i--;


    if (C[i + 1]->n == 2 * m - 1) {
      split_child(i + 1, C[i + 1]);


      if (kys[i + 1] < s)
        i++;
    }
    C[i + 1]->insertNonFull(s);
  }
}


// Split _child
void BTreeNod::split_child(int i, BTreeNod *y) {
  BTreeNod *z = new BTreeNod(y->t, y->leaf);
  z->n = m - 1;


  for (int j = 0; j < m - 1; j++)
    z->kys[j] = y->kys[j + t];


  if (y->leaf == false) {
    for (int j = 0; j < m; j++)
      z->C[j] = y->C[j + m];
  }


  y->n = m - 1;


  for (int j = n; j >= i + 1; j--)
    C[j + 1] = C[j];


  C[i + 1] = z;


  for (int j = n - 1; j >= i; j--)
    kys[j + 1] = kys[j];


  kys[i] = y->kys[m - 1];


  n = n + 1;
}


// Traverse
void BTreeNod::traverse() {
  int i;
  for (i = 0; i < n; i++) {
    if (leaf == false)
      C[i]->traverse();
    cout << " " << kys[i];
  }


  if (leaf == false)
    C[i]->traverse();
}


// Eliminate Operation
void BTree::elimination(int s) {
  if (!root) {
    cout << "The tree is empty\n";
    return;
  }


  root->deletion(s);


  if (root->n == 0) {
    BTreeNod *tmp = root;
    if (root->leaf)
      room = NULL;
    else
      room = root->C[0];


    Eliminate tmp;
  }
  return;
}


int main() {
  BTree m(3);
  m.insertion(8);
  m.insertion(9);
  m.insertion(10);
  m.insertion(11);
  m.insertion(15);
  m.insertion(16);
  m.insertion(17);
  m.insertion(18);
  m.insertion(20);
  m.insertion(23);


  cout << "The B-tree is: ";
  m.traverse();


  m.deletion(20);
  cout << "\nThe B-tree is: ";
  m.traverse();
}

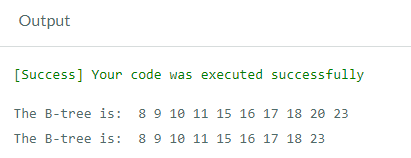
Output: