What is a Tree in Terms of a Graph?

To know the explanation of trees in terms of graphs, we need first to know what trees and graphs are. So let us first learn about trees and graphs.

Trees and graphs are types of non-linear data structures.

Note:

Data structures

A data structure is a form used intelligently and quickly to store, process, organize, and store data in a machine or computer format. Data structures help represent data for ease of use and manipulation.

Data structures are not just for storing data but also for processing, storage, and preservation. Almost every program or application contains basic and advanced data structures. We have many simple and advanced data structures, and finding a program in a programming language that does not have a data structure is complicated.

Non-linear Data structuresIn Non-linear data structures, content is not a series of information presented at different levels. There are several ways to pass indirectly from one element to another, and unauthorized data points are shared at least once.

Graph Data structure

The graph has two sets, considered V and E. These vertices are also called nodes, and edges are referred to as arcs connecting any two nodes in a graph. In a simple sentence, we can say that graph- is a set of vertices (V) and edges (E) which is denoted as G (V, E). These are usually accustomed to solving several real-time problems efficiently.

These represent networks like a city's telephones, circuitry, and paths. These are also used on many social platforms like Facebook, LinkedIn, etc. Let us consider an example of each user or person on Facebook as a vertex (or node) in the graph.

Each vertex has information about the user, like name, gender, etc., and the connection between each node or vertex is considered an edge or arc. These are also used in the operating system as resource location graphs.

These are also used in Google maps to find the shortest distance between two places, these are also used in airlines to know the best effective route, used in transportation, in circuits it is used to represent the nodes or circuitry points, these are used to solve challenging puzzles like mazes, these are also used in computer networking, there are many advantages of using graphs like it is straightforward to work with the algorithms like DFS and BFS, it has many practical applications, because of its nature(non-linear data structure) it is used in solving many complex problems, it helps in understanding and visualizing complex issues. As we know, every coin has the other side.

Advantages of graphs in data structures

1. Data is organized with the help of graphs.
2. Resource allocation graphs are used in operating systems.
3. Graphs are used in algorithms which include circuits. In these cases, the wires are represented by the edges, and the nodes represent the circuit points.
4. Neighbors of given nodes, the shortest paths between nodes, and many more can be easily found with the help of graphs.
5. As graphs are non-linear data structures, they help in problem visualization and understanding complex problems.
6. Google maps use graphs. The shortest route on the map is found in google maps using graphs.
7. Graphs are also used in algorithms used in games which include solving puzzles or mazes with one solution.
8. DFS (Depth first search) and BFS (Breadth-first search) algorithms are implemented using graphs.
9. In computers, their flow of control is represented using graphs.
10. Graphs are used in state transition diagrams. Their respective states and transitions are represented using graphs.
11. Computer networks that have peer-to-peer (P2P) applications use graphs.
12. Minimum spanning trees are identified with the help of graphs. These trees have many applications.
13. Social networking sites like Facebook, Instagram, etc., use graphs. On these websites, the users are treated as nodes, and the relations between them are treated as edges.
14. Graphs are also used in algorithms that help find the shortest transportation path.
15. Graphs are also used in blockchain that is used for cryptocurrency, and directed acyclic graphs (DAG) are used for these purposes. Nano, IOTA, and other cryptos mainly based on Directed acyclic graphs (DAG) can be examples of graph algorithms used in blockchains for cryptocurrency.

Tree Data structure

The Tree is a document editor and is a great way to organize your content and quickly transfer it to your computer. A tree data structure consists of child, structure, and root nodes associated with fields, and this data also contains leaves, branches, and related roots.

Advantages of trees in data structures

Tree data is organized into columns, groups, arrays, and linked lists. A tree is a hierarchical structure; A data model consists of nodes representing and supporting processes. Asynchronous data stores store different data types in a tree-like data structure called a root. All kinds of data are stored in a central location. Each line contains a message. The branches at the bottom of the Tree are called data models.

A tree is a hierarchical, non-linear file with nodes. Each tree section contains a table of values and store names that refer to other units ("Children"). Trees are considered non-linear because they are hierarchical. The data in the Tree is non-linear. But it is organized differently, more precisely, hierarchically.

A type of binary Tree. This is for security purposes only and is a private message. Since this data structure is a separate tree, it can have at most two children. A binary tree can always have 0, 1, or 2 children. A binary search tree can traverse a nested list and match its speed. This allows a binary tree to provide the benefits of a linked list and an array, making it easier to find hidden objects (since they are mutable data structures).

Advantages of trees in data structures

1. It takes an average time to perform any insertion and deletion operations in trees.
2. Data is represented in the hierarchical format in trees.
3. Keys can be organized as a tree (like in a BST (Binary search tree)). This helps search any given tree easier and quicker than Linked Lists. However, it is slower compared to arrays. Red-black trees and AVL (Adelson, Velskii & Landis Tree) are self-balancing search trees that guarantee an upper bound of O(log N) for search.
4. As the tree data structures are dynamic, the count of nodes forming the tree data structure is not limited.
5. The implementation of pointers in the tree data structure is similar to linked lists but differs from arrays. This means that the nodes are linked using pointers and do not have an upper limit.
6. As the tree data structures are dynamic, the count of nodes forming the tree data structure is not limited.
7. The tree data structure is used as a Decision tree.

Trees in terms of graph

Trees are the simplest graph forms, and they have a rich structure. Trees are a subpart of graphs with no loops or cycles. Trees in a graphical format represent a hierarchical structure. Trees have a vast range of applications starting from a simple family tree to thorny trees in data structures.

In technical terms, we can say that trees are connected acyclic graphs. This means that trees are graphs in which there are no loops and circles (i.e., there exists exactly one path between any two chosen nodes of the graph), and all the nodes are connected.

Note:

Connected graph

The graphs in which all the nodes are connected are called connected graphs. A connected graph has at least one path between any two chosen nodes.

Acyclic graph

The graphs in which no loops or circles are present are called acyclic graphs. In an acyclic graph, precisely one path exists between two chosen nodes.

Connected acyclic graphsThe graphs which come under both acyclic and connected graphs are called connected acyclic graphs.

Examples:

Given below are examples of trees:

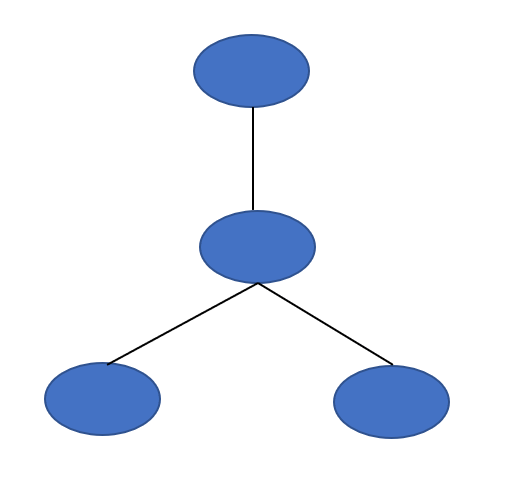
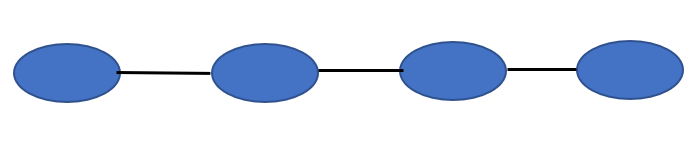
The above figures are examples of trees. We can observe that these are graphs with no cycles or loops, and all the nodes are connected, i.e., they are both connected and acyclic graphs (Connected acyclic graphs)