Insertion Sort vs Bubble Sort

In this article, we will see the major differences between Insertion Sort and Bubble Sort. Before that, let’s have a quick overview of what these sorting algorithms are and what’s the idea behind them.

What is Insertion Sort?

Insertion Sort – In Insertion sort, we select all elements of the unsorted array and place them at their correct position in the sorted array. After each iteration, the sorted array’s size increases and the unsorted array's size decreases. The pseudo-code of the insertion sort function is given below:

Insertion sort (a[], n)
{
	For j 1 to n-1
	{	
		Key = a[j]
		i = j - 1
		While i > -1 and a[i] > key
		{
			a[i + 1] = a[i]
			i = i – 1
		}
	a[i + 1] = Key
	}
} // Where n is the size of the array

The for-loop runs from 1 to n-1 and the while-loop runs from i = j-1 to 0. After complete execution of the internal while-loop, the element at the jth index is placed at its correct position in the sorted array.

Let’s understand the above idea through an example-

Consider an unsorted array a[] = {25, 10, 12, 18, 6}. Let’s apply insertion sort on it:

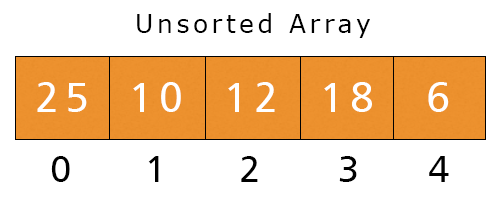
• First Iteration – j = 1, i = 0 to 0, and Key = a[j] = a[1] = 10
  • Here, i is greater than -1 and a[i = 0] = 25 > key = 10. The condition of while loop is satisfied, we place 25 at index 1, and decrement i by 1.

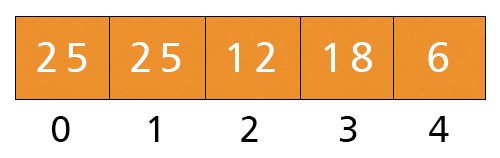
• Now, i is equal to -1, hence the condition is not satisfied. We execute the last statement. a[i + 1] = a[-1 + 1] = a[0] = Key = 10. Now, the array will be like as shown in figure.

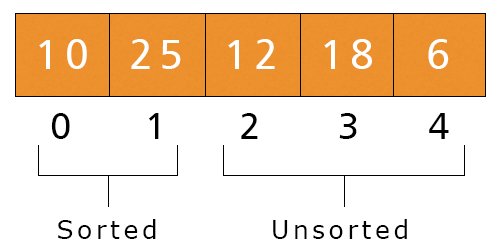
• Second Iteration – j = 2, i = 1 to 0, and Key = a[2] = 12.
  • Here, i = 1, a[i] = 25 > Key, the while-condition is satisfied. We execute a[1+1] = a[1] = 25 and i = 1-1 = 0.

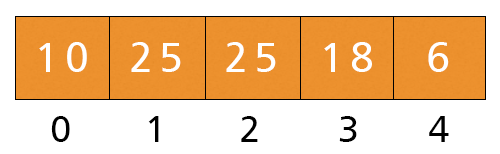
• Now, i = 0 and a[0] = 10 < key = 12. The while condition is not satisfied. We execute the last statement, a[i+1] = a[0+1] = 12.

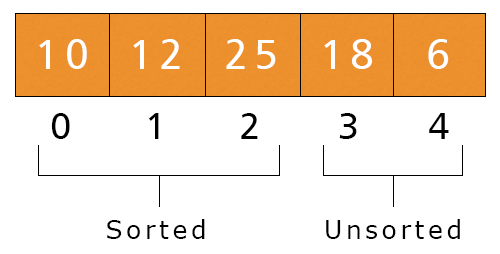
• Third Iteration – j = 3, i = 2 to 0, and Key = a[3] = 18
  • Here, i = 2, a[i] = 25 > Key = 18. The while condition is satisfied. We execute a[2+1] = a[2] = 25 and i = 2 - 1 = 1

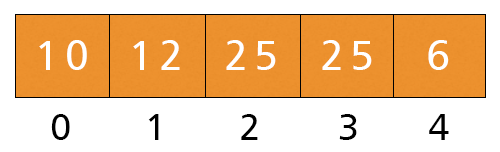
• Now, i = 1, a[i] = 12 < Key = 18. The while condition is not satisfied. We execute the last statement, a[i + 1] = a[1 + 1] = 18.

• Fourth Iteration – j = 4, i = 3 to 0, and Key = a[4] = 6.
  • Here, i = 3, a[i] = 25 > Key = 6. The while condition is satisfied. We execute a[3 + 1] = a[3] = 25 and i = 3 - 1 = 2.

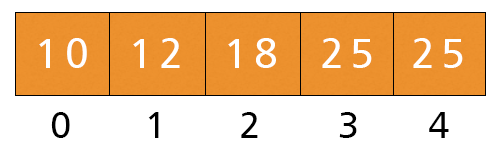
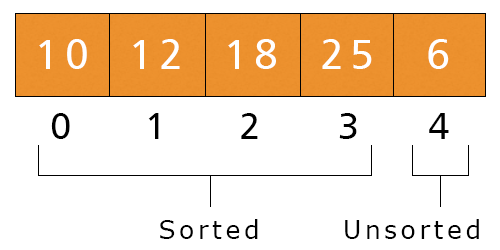
• Now, i = 2, a[i] = 18 > Key = 6. The while condition is satisfied. We execute a[2 + 1] = a[2] = 18 and i = 2 - 1 = 1.

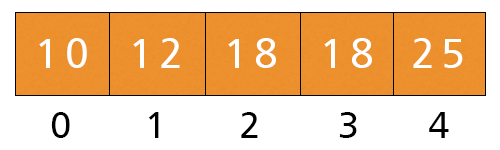
• Now, i = 1, a[i] = 12 > Key = 6. The while condition is satisfied. We execute a[1 + 1] = a[1] = 12 and i = 1 - 1 = 0.

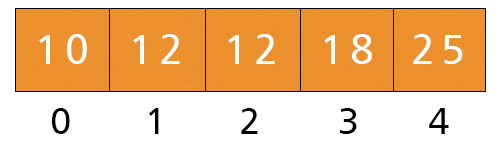
• Now, i = 0, a[i] = 10 > Key = 6. The while condition is satisfied. We execute a[0 + 1] = a[0] = 10 and i = 0 - 1 = -1.

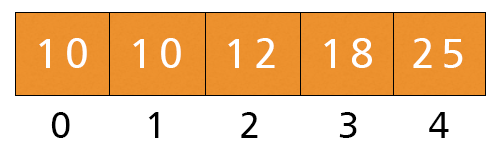
• Now, i is equal to -1, hence the condition is not satisfied. We execute the last statement. a[i + 1] = a[-1 + 1] = a[0] = Key = 6. Now, the array will be like as shown in figure.

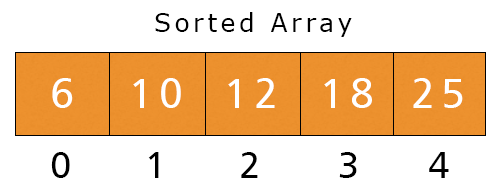
After complete execution of the 4^th iteration, we get our sorted array.

What is Bubble Sort?

Bubble Sort – In bubble sort, it continuously compares two adjacent elements and swaps them if they are not in the right order on each iteration. On each pass, it places the largest value at the end of the unsorted array. The pseudo-code of the bubble sort function is given below:

Bubble Sort (int a[], int n)
{
	For i =1 to n-1
	{
		for j = 0 to n - i – 1
		{
			If a[j] > a[j + 1]
				swap (a[j], a[j + 1])
		}
	}
} // Where n is the size of the array

We can clearly see in the above pseudo-code that the external for loop starts from 1 and ends at n - 1, and the internal for-loop starts from 0 and ends at n - i - 1.

Let’s understand the above idea through an example:

Consider an unsorted array a[5] = {25, 10, 12, 18, 6}. Let’s sort this array using bubble sort.

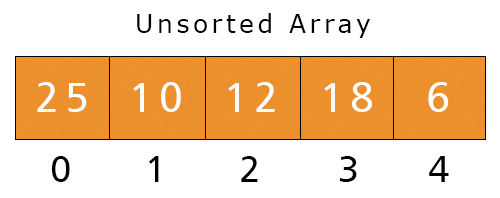
• First Iteration – i = 1, j 0 to n – 1 – 1 = 3.
  • j = 0. Here, a[0] = 25 and a[1] = 10 and 25 > 10, If-condition is satisfied, we swap these values.

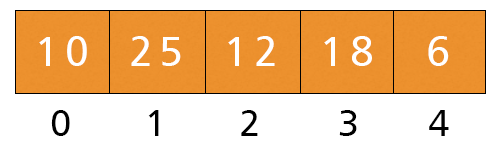
• j = 1. Here, a[1] = 25 and a[2] = 12 and 25 > 12, If-condition is satisfied, we swap these values.

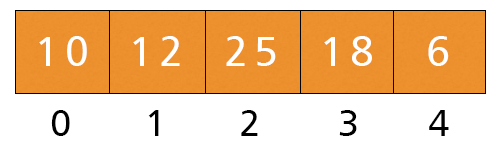
• j = 2. Here, a[2] = 25 and a[3] = 18 and 25 > 18, If-condition is satisfied, we swap these values:

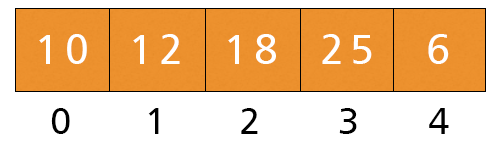
• j = 3. Here, a[3] = 25 and a[4] = 6 and 25 > 16, If-condition is satisfied, we swap these values:

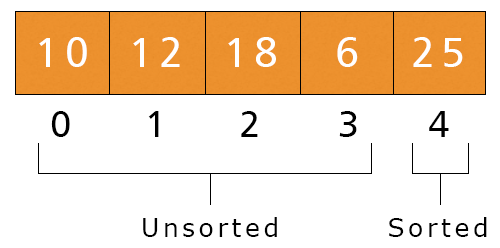
• Second Iteration – i = 2, j = 0 to 2
  • j = 0. Here, a[0] = 10 and a[1] = 12 and 10 < 12, If-condition is not satisfied, no swapping occurs:

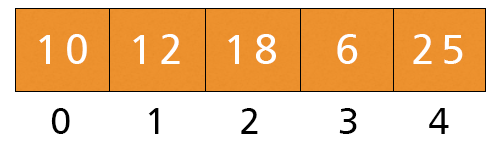
• j = 1. Here, a[1] = 12 and a[2] = 18 and 12 < 18, If-condition is not satisfied, no swapping occurs:

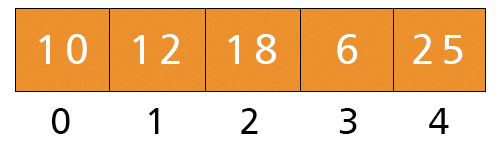
• j = 2. Here, a[2] = 18 and a[3] = 6 and 18 > 6, If-condition is satisfied, we swap these values:

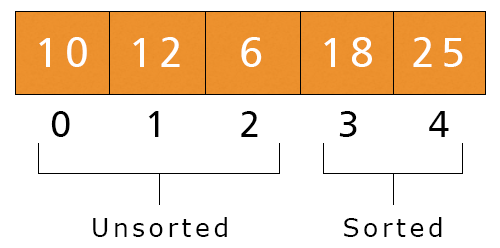
• Third Iteration – i = 3, j 0 to 1
  • j = 0. Here, a[0] = 10 and a[1] = 12 and 10 < 12, If-condition is not satisfied, no swapping occurs:

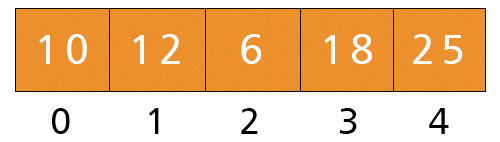
• j = 1. Here, a[1] = 12 and a[2] = 6 and 12 > 6, If-condition is satisfied, we swap these values:

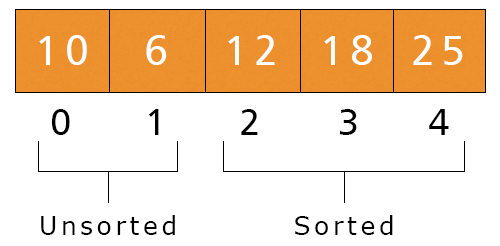
• Fourth Iteration – i = 4, j 0 to 0
  • j = 0. Here, a[0] = 10 and a[1] = 6 and 10 > 6, If-condition is satisfied, we swap these values.

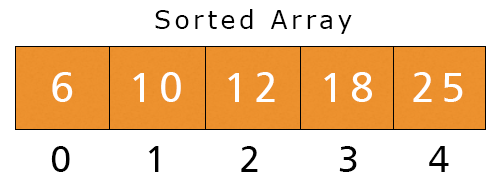
After complete execution of the external for loop, we get a sorted array.

Differences between Insertion Sort and Bubble Sort:

The main differences between these two sorting techniques are listed below in the table:

	Insertion Sort			Bubble Sort
Idea/ Approach	The idea is to insert an element of the unsorted array at its correct position in the sorted array.			The idea is to compare every place and place them in the right order.
Time Complexity	Best	Average	Worst	Best	Average	Worst
	T(n) = O(n)	T(n) = O(n^2)	T(n) = O(n^2)	T(n) = O(n)	T(n) = O(n^2)	T(n) = O(n^2)
Space Complexity	Worst Case: T(n) = O(1)			Worst Case: T(n) = O(1)
Efficiency	More efficient than the Bubble Sort.			Less Efficient than the Insertion Sort
Speed	Faster than the Bubble Sort as less comparison and swapping occur.			Slower than the Insertion sort as more comparisons and swapping occur.
Stability	Stable – Element’s orders remain preserved			Stable – Element’s Orders remain preserved
Method	The insertion method is used to sort an array.			The comparison method is used to sort an array.