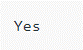Implementation

// Writing a C++ program to analyze whether the given binary search tree contains a dead end. 
#include<bits/stdc++.h>
using namespace std;


// creating a binary search tree node
struct __nod
{
	int record;
	struct __nod *Lft, *Rt;
};


// A utility function to create a new node
__nod *new__nod(int record)
{
	__nod *temp = nw __nod;
	temp->record = record;
	temp->Lft = temp->Rt = NILL;
	return temp;
}


/* creating a utility function to insert a new node with the given set of keys in a binary search tree. */
struct __nod* insert(struct __nod* __nod, int ky)
{
	/* In case the tree appears empty, we have to return a new node. */
	if (__nod == NILL) return new__nod(ky);


	/* or we have to perform recursion down the tree*/
	if (ky < __nod->record)
		__nod->Lft = insert(__nod->Lft, ky);
	else if (ky > __nod->record)
		__nod->Rt = insert(__nod->Rt, ky);


	/* we have to return the unchanged pointer of the node */
	return __nod;
}
// writing a function that will store all the nodes of the given binary tree. 
void store__nods(__nod * root, Unord_set<int> &all___nods,
						Unord_set<int> &leaf___nods)
{
	if (root == NILL)
		return ;


	// we have to store all the nodes of the binary search tree
	all___nods.insert(root->record);


	// now we have to store the leaf node in hash
	if (root->Lft==NILL && root->Rt==NILL)
	{
		leaf___nods.insert(root->record);
		return ;
	}


	// now we have to recur down the call test cases
	store__nods(root-> Lft, all___nods, leaf___nods);
	store__nods(root->Rt, all___nods, leaf___nods);
}


// we have to return the true value if there is a dead end in the tree; otherwise, we can return the false value. 
bool isDeadEnd(__nod *root)
{
	// writing the basic case
	if (root == NILL)
		return false ;


	//Now, we will originate two empty hash sets, which will help us store the elements of the binary search tree and leaf nodes, respectively.  
	Unord_set<int> all___nods, leaf___nods;


	//Now we have to insert the 0 value in all the nodes to handle a case and if the binary tree contains 1 value.
	all___nods.insert(0);


	// we have to call the store node function to store all the binary search tree nodes. 
	store__nods(root, all___nods, leaf___nods);


	// we have to traverse the leaf node and check whether the tree contains a continuous sequence of size tree or not 
	for (auto i = leaf___nods.begin(); i != leaf___nods.end(); i++)
	{
		int x = (*i);


		// Here, we check the first and the last element of
		// continuous sequence that are x-1 & x+1
		if (all___nods.find(x+1) != all___nods.end() &&
			all___nods.find(x-1) != all___nods.end())
			return true;
	}


	return false ;
}


// writing the main program to test the above functions
int main()
{
/*	 8
	/ \
	5 11
	/ \
	2 7
	\
	3
	\
		4 */
	__nod *root = NILL;
	root = insert(root, 8);
	root = insert(root, 5);
	root = insert(root, 2);
	root = insert(root, 3);
	root = insert(root, 7);
	root = insert(root, 11);
	root = insert(root, 4);
	if (isDeadEnd(root) == true)
		cout << "Yes " << endl;
	else
		cout << "No " << endl;
	return 0;
}

Output:

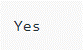
Finding a Deadlock in a Binary Search Tree

Example 2

// Writing a Java program to analyze whether the given binary search tree contains a dead end or not. 
import java.util.*;


class Main {
	// create two empty hash sets that store all
	// BST elements and leaf nodes, respectively.
	static HashSet<Integer> all___nods
		= new HashSet<Integer>();
	static HashSet<Integer> leaf___nods
		= new HashSet<Integer>();
/* creating a utility function to insert a new node with the given set of keys in a binary search tree. */


	public static __nod insert(__nod __nod, int ky)
	{
	/* In case the tree appears empty, we have to return a new node. */
		if (__nod == NILL)
			return new __nod(ky);
	/* or we have to perform recursion down the tree*/
		if (ky < __nod.record)
			__nod.Lft = insert(__nod.Lft, ky);
		else if (ky > __nod.record)
			__nod.Rt = insert(__nod.Rt, ky);
	/* we have to return the unchanged pointer of the node */
		return __nod;
	}
	// writing a function that will store all the nodes of the given binary tree.
	public static void store__nods(__nod root)
	{
		if (root == NILL)
			return;


	// we have to store all the nodes of the binary search tree
		all___nods.add(root.record);


	// now we have to store the leaf node in hash
		if (root.Lft == NILL && root.Rt == NILL) {
			leaf___nods.add(root.record);
			return;
		}
// now we have to recur down the call test cases
		store__nods(root.Lft);
		store__nods(root.Rt);
	}


	// we have to return the true value if there is a dead end in the tree; otherwise, we can return the false value. 
	public static boolean isDeadEnd(__nod root)
	{
	// writing the basic case
		if (root == NILL)
			return false;


		//Now, we will originate two empty hash sets, which will help us in storing the elements of the binary search tree and leaf nodes, respectively.  
		all___nods.add(0);


		//Now we have to insert the 0 value in all the nodes to handle a case and if the binary tree contains 1 value.


		store__nods(root);
	// we have to call the store node function to store all the binary search tree nodes. 


		for (int i: leaf___nods) {
			int x = i;


			// Here, we check the first and the last element of
			// continuous sequence that are x-1 & x+1
			if (all___nods.contains(x + 1)
				&& all___nods.contains(x - 1)) {
				return true;
			}
		}
		return false;
	}
// writing the main program to test the above functions
	public static void main(String[] args)
	{
		/*	 8
			/ \
			5 11
			/ \
			2 7
			\
			3
			\
				4 */
		__nod root = NILL;
		root = insert(root, 8);
		root = insert(root, 5);
		root = insert(root, 2);
		root = insert(root, 3);
		root = insert(root, 7);
		root = insert(root, 11);
		root = insert(root, 4);
		if (isDeadEnd(root) == true)
			System.out.println("Yes");


		else
			System.out.println("No");
	}
}


// A BST __nod
class __nod {
	int record;
	__nod Lft, Rt;


	__nod(int record)
	{
		this.record = record;
		Lft = NILL;
		Rt = NILL;
	}
}

Output:

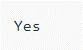
Example 3

# Writing a Python program to analyze whether the given binary search tree contains a dead end or not. 
all___nods = set()
leaf___nods = set()


# Creating a binary search tree node
class new__nod:


	def __init__(self, record):


		self.record = record
		self.Lft = None
		self.Rt = None


// A utility function to create a new node
def insert(__nod, ky):
	/* In case the tree appears empty, we have to return a new node. */
	if (__nod == None):
		return new__nod(ky)
/* or we have to perform recursion down the tree*/
	if (ky < __nod.record):
		__nod.Lft = insert(__nod.Lft,
						ky)
	elif (ky > __nod.record):
		__nod.Rt = insert(__nod.Rt,
							ky)


	# we have to return the unchanged pointer of the node 
	return __nod


# Writing a function that will store all the nodes of the given binary tree. 
def store__nods(root):


	global all___nods
	global leaf___nods
	if (root == None):
		return


	# We have to store all the nodes of the binary search tree
	all___nods.add(root.record)


	# Now we have to store the leaf node in hash
	if (root.Lft == None and
			root.Rt == None):
		leaf___nods.add(root.record)
		return


	# Now we have to recur down the call test cases
	store__nods(root. Lft)
	store__nods(root.Rt)


# We have to return the true value if there is a dead end in the tree; otherwise, we can return the false value. 
def isDeadEnd(root):


	global all___nods
	global leaf___nods


	# Writing the basic case
	if (root == None):
		return False


	# Now, we will originate two empty hash sets, which will help us store the elements of the binary search tree and leaf nodes, respectively.  
	# We must insert the 0 value in all the nodes to handle a case and if the binary tree contains one value.
	all___nods.add(0)


	# We have to call the store node function to store all the binary search tree nodes. 
	store__nods(root)


	# We have to traverse the leaf node and check whether the tree contains a continuous sequence of size tree or not 
	for x in leaf___nods:


		# Here, we check first and
		# last element of continuous
		# sequence that are x-1 & x+1
		if ((x + 1) in all___nods and
				(x - 1) in all___nods):
			return True


	return False




# Writing the main program to test the above functions
if __name__ == '__main__':


	'''/*	 8
	/ \
	5 11
	/ \
	2 7
	\
	3
	\
		4 */
	'''
	root = None
	root = insert(root, 8)
	root = insert(root, 5)
	root = insert(root, 2)
	root = insert(root, 3)
	root = insert(root, 7)
	root = insert(root, 11)
	root = insert(root, 4)


	if(isDeadEnd(root) == True):
		print("Yes")
	else:
		print("No")
# Writing a Python program to analyze whether the given binary search tree contains a dead end or not. 
all___nods = set()
leaf___nods = set()


# Creating a binary search tree node
class new__nod:


	def __init__(self, record):


		self.record = record
		self.Lft = None
		self.Rt = None


// A utility function to create a new node
def insert(__nod, ky):
	/* In case the tree appears empty, we have to return a new node. */
	if (__nod == None):
		return new__nod(ky)
/* or we have to perform recursion down the tree*/
	if (ky < __nod.record):
		__nod.Lft = insert(__nod.Lft,
						ky)
	elif (ky > __nod.record):
		__nod.Rt = insert(__nod.Rt,
							ky)


	# we have to return the unchanged pointer of the node 
	return __nod


# Writing a function that will store all the nodes of the given binary tree. 
def store__nods(root):


	global all___nods
	global leaf___nods
	if (root == None):
		return


	# We have to store all the nodes of the binary search tree
	all___nods.add(root.record)


	# Now we have to store the leaf node in hash
	if (root.Lft == None and
			root.Rt == None):
		leaf___nods.add(root.record)
		return


	# Now we have to recur down the call test cases
	store__nods(root. Lft)
	store__nods(root.Rt)


# We have to return the true value if there is a dead end in the tree; otherwise, we can return the false value. 
def isDeadEnd(root):


	global all___nods
	global leaf___nods


	# Writing the basic case
	if (root == None):
		return False


	# Now, we will originate two empty hash sets, which will help us store the elements of the binary search tree and leaf nodes, respectively.  
	# We must insert the 0 value in all the nodes to handle a case and if the binary tree contains one value.
	all___nods.add(0)


	# We have to call the store node function to store all the binary search tree nodes. 
	store__nods(root)


	# We have to traverse the leaf node and check whether the tree contains a continuous sequence of size tree or not 
	for x in leaf___nods:


		# Here, we check first and
		# last element of continuous
		# sequence that are x-1 & x+1
		if ((x + 1) in all___nods and
				(x - 1) in all___nods):
			return True


	return False


# Writing the main program to test the above functions
if __name__ == '__main__':


	'''/*	 8
	/ \
	5 11
	/ \
	2 7
	\
	3
	\
		4 */
	'''
	root = None
	root = insert(root, 8)
	root = insert(root, 5)
	root = insert(root, 2)
	root = insert(root, 3)
	root = insert(root, 7)
	root = insert(root, 11)
	root = insert(root, 4)


	if(isDeadEnd(root) == True):
		print("Yes")
	else:
		print("No")

Output:

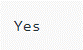
Example 4

// Writing a C++ program to analyze whether the given binary search tree contains a dead end. 
#include<bits/stdc++.h>
using namespace std;
// creating a binary search tree node
struct __nod
{
	int record;
	struct __nod *Lft, *Rt;
};
// A utility function to create a new node
__nod *new__nod(int record)
{
	__nod *temp = nw __nod;
	temp->record = record;
	temp->Lft = temp->Rt = NILL;
	return temp;
}
/* creating a utility function to insert a new node with the given keys in a binary search tree. */
struct __nod* insert(struct __nod* __nod, int ky)
{
	/* In case the tree appears empty, we have to return a new node. */
	if (__nod == NILL) return new__nod(ky);
	/* or we have to perform recursion down the tree*/
	if (ky < __nod->record)
		__nod->Lft = insert(__nod->Lft, ky);
	else if (ky > __nod->record)
		__nod->Rt = insert(__nod->Rt, ky);
	/* we have to return the unchanged pointer of the node */
	return __nod;
}
void findall__nods(__nod* root,map<int,int> &all__nods)
{
	if(root == NILL)
	return ;
	
	all__nods[root->record] = 1;
	findall__nods(root->Lft,all__nods);
	findall__nods(root->Rt,all__nods);
}
bool check(__nod* root,map<int,int> &all__nods)
{
	if(root == NILL)
	return false;
	
	if(root->Lft == NILL and root->Rt == NILL)
	{
		int pre = root->record - 1;
		int next = root->record + 1;


		if(all__nods.find(pre) != all__nods.end() and all__nods.find(next) != all__nods.end())
		return true;
	}
	
	return check(root->Lft,all__nods) or check(root->Rt,all__nods);
	
}
bool isDeadEnd(__nod *root)
{
	// writing the basic case


if (root == NILL)
		return false ;
	map<int,int> all__nods;
	// adding 0 for handling the exception of a node having record = 1
	all__nods[0] = 1;
	findall__nods(root,all__nods);
	
	return check(root,all__nods);
	
}
// writing the main program to test the above functions
int main()
{
/*	 8
	/ \
	5 11
	/ \
	2 7
	\
	3
	\
		4 */
	__nod *root = NILL;
	root = insert(root, 8);
	root = insert(root, 5);
	root = insert(root, 2);
	root = insert(root, 3);
	root = insert(root, 7);
	root = insert(root, 11);
	root = insert(root, 4);
	if (isDeadEnd(root) == true)
		cout << "Yes " << endl;
	else
		cout << "No " << endl;
	return 0;
}

Output:

Data Structures Tutorial

Misc Topic:

Data Structures Tutorial

Misc Topic:

Finding a Deadlock in a Binary Search Tree

Implementation