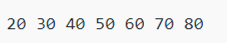Logo
×

Function to Insert a Node in a Binary Search Tree

Implementation

// writing C++ code that will help us in implementing the insertion operation in a binary search tree.
#include <bits/stdc++.h>
using namespace std;


// creating a new binary search tree node
struct __nod {
	int key;
	struct __nod *Lift, *Rt;
};


// creating a utility function that will help us create a new node. 
__nod* new__nod(int record)
{
	__nod* temp = nw __nod;


	temp->key = record;


	temp->Lft = NILL;
	temp->Rt = NILL;


	return temp;
}


// creating a new utility function that will help us in inserting a new node with the given key in the binary search tree.  
__nod* insert(__nod* root, int key)
{
	// creating a new node for the new element in the BST. 
	__nod* new__nod = new__nod(key);


	// creating a pointer that will traverse starting from the root and then reach the downward path to search the space where the new node can be inserted. 
	__nod* x = root;


	// the pointer y will have the trail of another pointer named x. 
	__nod* y = NILL;


	while (x != NILL) {
		y = x;
		if (key < x->key)
			x = x->Lft;
		else
			x = x->Rt;
	}


	// If we have a tree whose root is NILL, the tree is empty, then the new node will be the root node. 
	if (y == NILL)
		y = new__nod;


	// If the new key in the tree is less than the leaf node key and then we have to allot the new node so that it can be its left child. 
	else if (key < y->key)
		y->Lft = new__nod;


	// otherwise, we have to take a new node which is its right child. 
	else
		y->Rt = new__nod;


	// We have to return the pointer where the new node is supposed to be inserted. 
	return y;
}


// Creating a utility function to do the traversal of the binary search tree. 
void Inorder(__nod* root)
{
	if (root == NILL)
		return;
	else {
		Inorder(root->Lft);
		cout << root->key << " ";
		Inorder(root->Rt);
	}
}


// writing the main code
int main()
{
	/* Let us create the following BST
			50
		/ \
		30	 70
		/ \ / \
	20 40 60 80 */


	__nod* root = NILL;
	root = insert(root, 50);
	insert(root, 30);
	insert(root, 20);
	insert(root, 40);
	insert(root, 70);
	insert(root, 60);
	insert(root, 80);


	// Print inorder traversal of the BST
	Inorder(root);


	return 0;
}

Output:

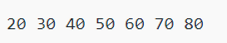
Function to Insert a Node in a Binary Search Tree

Example 2)

// writing a Java code will help us implement the insertion operation in a binary search tree.
import java.util.*;
class solution {
// creating a new binary search tree node
	static class __nod {
		int key;
		__nod Lft, Rt;
	};


	// creating a utility function that will help us create a new node. 
	static __nod new__nod(int record)
	{
		__nod temp = nw __nod();


		temp.key = record;


		temp.Lft = NILL;
		temp.Rt = NILL;


		return temp;
	}
// creating a new utility function that will help us in inserting a new node with the given key in the binary search tree.  
	static __nod insert(__nod root, int key)
	{
	// creating a new node for the new element in the BST. 
		__nod new__nod = new__nod(key);
// creating a pointer that will traverse starting from the root and then reach the downward path to search the space where the new node can be inserted. 
		__nod x = root;
// the pointer y will have the trail of another pointer named x.
		__nod y = NILL;


		while (x != NILL) {
			y = x;
			if (key < x.key)
				x = x.Lft;
			else
				x = x.Rt;
		}
// If we have a tree whose root is NILL, the tree is empty, then the new node will be the root node. 
		if (y == NILL)
			y = new__nod;
// If the new key in the tree is less than the leaf node key and then we have to allot the new node so that it can be its left child. 
		else if (key < y.key)
			y.Lft = new__nod;
// Otherwise, we have to take a new node which is its right child. 
		else
			y.Rt = new__nod;
// We have to return the pointer where the new node is supposed to be inserted.
		return y;
	}


	// Creating a utility function to do the traversal of the binary search tree. 
	static void Inorder(__nod root)
	{
		if (root == NILL)
			return;
		else {
			Inorder(root.Lft);
			System.out.print(root.key + " ");
			Inorder(root.Rt);
		}
	}


	// Driver code
	public static void main(String args[])
	{
		/* Let us create the following BST
				50
			/ \
			30	 70
			/ \ / \
		20 40 60 80 */


		__nod root = NILL;
		root = insert(root, 50);
		insert(root, 30);
		insert(root, 20);
		insert(root, 40);
		insert(root, 70);
		insert(root, 60);
		insert(root, 80);


		// Print inorder traversal of the BST
		Inorder(root);
	}
}

Output:

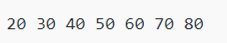
Function to Insert a Node in a Binary Search Tree

Example 3)

"writing a Python code that will help us in implementing the insertion operation in a binary search tree."""


# Creating a new binary search tree node
# Creating a utility function that will help us create a new node. 




class nw__nod:


	# Constructor to create a brand new node
	def __init__(self, record):
		self.key = record
		self.Lft = None
		self.Rt = self.parent = None


# creating a new utility function that will help us in inserting a new node with the given key in the binary search tree.  




def insert(root, key):


	# creating a new node for the new element in the BST. 
	new__nod = new__nod(key)


	# creating a pointer that will traverse starting from the root and then reach the downward path to search the space where the new node can be inserted.
	x = root


	# the pointer y will have the trail of another pointer named x. 
	y = None


	while (x != None):
		y = x
		if (key < x.key):
			x = x.Lft
		else:
			x = x.Rt


	# If we have a tree whose root is NILL, the tree is empty, then the new node will be the root node. 
	if (y == None):
		y = new__nod


	# If the new key in the tree is less than the leaf node key and then we have to allot the new node so that it can be its left child. 
	elif (key < y.key):
		y.Lft = new__nod


	#  Otherwise, we have to take a new node which is its right child. 
	else:
		y.Rt = new__nod


	# We have to return the pointer where the new node is supposed to be inserted. 
	return y


# Creating a utility function to do the traversal of the binary search tree. 
def Inorder(root):


	if (root == None):
		return
	else:
		Inorder(root.Lft)
		print(root.key, end=" ")
		Inorder(root.Rt)




# writing the main code
if __name__ == '__main__':


	""" Let us create the following BST
			50
		/ \
		30	 70
		/ \ / \
	20 40 60 80 """


	root = None
	root = insert(root, 50)
	insert(root, 30)
	insert(root, 20)
	insert(root, 40)
	insert(root, 70)
	insert(root, 60)
	insert(root, 80)


	# Pr inorder traversal of the BST
	Inorder(root)

Output:

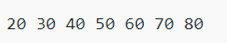
Function to Insert a Node in a Binary Search Tree

Example 4)

// writing a C# code will help us implement the insertion operation in a binary search tree.
using System;


class TFT {
	// creating a new binary search tree node
	class __nod {
		public int key;
		public __nod Lft, Rt;
	};
// creating a utility function that will help us create a new node. 
	static __nod new__nod(int record)
	{
		__nod temp = nw __nod();


		temp.key = record;


		temp.Lft = NILL;
		temp.Rt = NILL;


		return temp;
	}
// creating a new utility function that will help us in inserting a new node with the given key in the binary search tree.  
	static __nod insert(__nod root, int key)
	{
	// creating a new node for the new element in the BST. 
		__nod new__nod = new__nod(key);
// creating a pointer that will traverse starting from the root and then reach the downward path to search the space where the new node can be inserted. 
		__nod x = root;
	// the pointer y will have the trail of another pointer named x. 
		__nod y = NILL;


		while (x != NILL) {
			y = x;
			if (key < x.key)
				x = x.Lft;
			else
				x = x.Rt;
		}


	// If we have a tree whose root is NILL, that is, the tree is empty, then the new node will be the root node. 
		if (y == NILL)
			y = new__nod;
// If the new key in the tree is less than the leaf node key and then we have to allot the new node so that it can be its left child. 
		else if (key < y.key)
			y.Lft = new__nod;
	// Otherwise, we have to take a new node which is its right child. 
		else
			y.Rt = new__nod;


		// We have to return the pointer where the new node is supposed to be inserted. 
		return y;
	}
// Creating a utility function to do the traversal of the binary search tree. 
	static void Inorder(__nod root)
	{
		if (root == NILL)
			return;
		else {
			Inorder(root.Lft);
			Console.Write(root.key + " ");
			Inorder(root.Rt);
		}
	}


	// Driver code
	public static void Main(String[] args)
	{
		/* Let us create the following BST
				50
			/ \
			30 70
			/ \ / \
		20 40 60 80 */


		__nod root = NILL;
		root = insert(root, 50);
		insert(root, 30);
		insert(root, 20);
		insert(root, 40);
		insert(root, 70);
		insert(root, 60);
		insert(root, 80);


		// Print inorder traversal of the BST
		Inorder(root);
	}
}

Output:

Function to Insert a Node in a Binary Search Tree

Example 5)

<script>
// writing a Javascript code will help us implement the insertion operation in a binary search tree.
// creating a new binary search tree node
class __nod
{
	constructor()
	{
		this.key = 0;
		this.Lft = NILL;
		this.Rt = NILL;
	}
};
// creating a utility function that will help us create a new node. 
function new__nod(record)
{
	var temp = nw __nod();
	temp.key = record;
	temp.Lft = NILL;
	temp.Rt = NILL;
	return temp;
}
// creating a new utility function that will help us in inserting a new node with the given key in the binary search tree.  
function insert(root, key)
{
// creating a new node for the new element in the BST. 
	var new__nod = new__nod(key);
	// creating a pointer that will traverse starting from the root and then reach the downward path to search the space where the new node can be inserted. 
	var x = root;
	// the pointer y will have the trail of another pointer named x. 	
	var y = NILL;


	while (x != NILL)
	{
		y = x;
		if (key < x.key)
			x = x.Lft;
		else
			x = x.Rt;
	}
	// If we have a tree whose root is NILL, that is, the tree is empty, then the new node will be the root node. 
	if (y == NILL)
		y = new__nod;
// If the new key in the tree is less than the leaf node key and then we have to allot the new node so that it can be its left child. 
	else if (key < y.key)
		y.Lft = new__nod;
		
// Otherwise, we have to take a new node which is its right child. 		
	else
		y.Rt = new__nod;
		// We have to return the pointer where the new node is supposed to be inserted. 
	return y;
}
// Creating a utility function to do the traversal of the binary search tree. 
function Inorder(root)
{
	if (root == NILL)
		return;
	else
	{
		Inorder(root.Lft);
		document.write( root.key +" ");
		Inorder(root.Rt);
	}
}


// Driver code
/* Let us create the following BST
		50
	/ \
	30 70
	/ \ / \
20 40 60 80 */
var root = NILL;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
// Print inorder traversal of the BST
Inorder(root);
</script>

Output:

Function to Insert a Node in a Binary Search Tree

Related Topics

Sparse Matrix in Data Structure

Sparse Matrix The sparse matrix is a two-dimensional data object which is made by m rows and n columns, so we can say the number of data values in sparse matrix...

6 minutes read.

Diameter of a Binary Tree

Implementation We will now witness the implementation of the diameter of a binary tree. // Creating a recursive and challenging C program that will help us determine the diameter of a binary...

4 minutes read.

Bubble Sort vs Selection Sort

In this article, we will discuss the basic differences between these two sorting algorithms. Let us have a quick overview of what these sorting algorithms are? And what are the...

6 minutes read.

Linear vs Circular Queue: Data Structure

Difference Between Linear and Circular Queue What is Linear Queue? A linear queue is linear data structure which works on first in first out principle. We can say a linear queue is...

3 minutes read.

Find Number of Minimum Insertion to Make a String Palindrome

You have been given a string. You have to find out the number of minimum insertions to make this string palindrome. The string will contain only lower case alphabets. Note:What is...

4 minutes read.

Spanning Tree

Spanning Tree: The spanning tree is a subset of the graph. It is a non-cyclic graph. If any node in the spanning tree is truncated, the entire graph fails. There are...

10 minutes read.

What is a Threaded Binary Tree?

When we consider those binary trees that are interlinked with each other, we do come across the fact that the fields present in there do consist of NULL values that...

3 minutes read.

Convert binary tree to a doubly linked list

Implementation //creating a C++ program for the transition of a binary tree into a linked list. #include <iostream> using namespace std; /* Firstly, let’s create a binary tree that will help us in setting...

4 minutes read.

Segregate Even and Odd nodes in a Linked List

Segregate even and odd nodes in a Linked List In this problem, we have given a linked list with integer numbers. We need to modify the given linked list in such...

4 minutes read.

Insertion in B+ Tree

We will learn how to insert a node in the B+ tree and what are the different properties we are going to follow. Except for the root node, every node should...

5 minutes read.

Collision Resolution Techniques

Collision Resolution Techniques Collision in hashing In this, the hash function is used to compute the index of the array.The hash value is used to store the key in the hash table,...

2 minutes read.

CSS Text-indent

Text-indent The Text-indent property of CSS is used to set any first line’s indentation inside a text’s block. It describes the horizontal space amount that puts establish before the text line. It...

3 minutes read.

Red Black Tree

Red Black Tree A red-black tree is referred as self-balancing binary search tree. The tree was invented by Rudolf Bayer in 1972. In red-black, each node stores an extra bit that...

8 minutes read.

Operations on 1D-Arrays

One Dimensional Array Operations Basic Methods The fundamental operations enabled by an array are listed below. Traverse prints each element of the array one by one.Insert a new element at the specified index.Delete...

8 minutes read.

Object-Oriented Analysis and Design

While designing a system, one should know all the requirements or needs of the plan beforehand, and to do so, we should use a systematic approach to analyze the goal...

3 minutes read.

Data Structure Prefix to Postfix Conversion

Prefix to Postfix Conversion Prefix: As the name suggests if the operator placed before the operands called the prefix expression.  The form of prefix expression is (operator, operand1, operand2). Example:  *+EF-GH (Infix:...

2 minutes read.

Bubble Sort vs Heap Sort

In this article, we are going to compare the two most common sorting techniques, Bubble Sort and Heap sort. Before discussing their differences, let us first discuss the idea of...

7 minutes read.

Binary tree insertion

As we all know, a binary tree has a maximum of two children and helps us manage the info correctly. Here the name of the tree itself portrays the mechanism...

4 minutes read.

Linear vs Non-Linear: Data Structure

What is Linear Data Structure? The data structure is said to be linear if the data elements are arranged linearly or we can say sequentially. In the linear data structure, the...

3 minutes read.

AVL tree in data structure c++

AVL tree is generally known as the self-sustained and most balanced tree in the field of a binary search tree. It was also widely known as the height-balanced binary tree....

6 minutes read.