Binary Search
Binary Search: When there is a large data structure, the linear search takes a lot of time to search the element. The binary search was developed to overcome the lack of a linear search. It is based on the divide & conquers principle. It is a very fast searching algorithm. The time complexity of the binary search is O (log n). A binary search can only be applied to a sorted list.
In this searching technique, the given element is compared with the middle element of the list.
- If both elements are equal, it returns the index value.
- If both elements are not equal, we check whether the given element is larger or smaller than the middle element.
- If the given element is smaller than the middle element, we will repeat the same process in the smaller part of the list.
- If the given element is larger than the middle element, we will repeat the same process in the larger part of the list.
Complexity of Binary search
| Complexity | Best case | Average case | Worst case |
| Time | O(1) | O(log n) | O(log n) |
| Space | O(1) |
Algorithm of Binary search
| Binary_Search( ) Step 1: SET BEG = lower_bound, END = upper_bound, FLAG = - 1 Step 2: Repeat Steps 3 and 4 while BEG <=END Step 3: SET MID = (BEG + END)/2 Step 4: if A[MID] = VAL SET FLAG = MID print “index value of the element” Go to Step 6 else if A[MID] > VAL else END = MID - 1 else SET BEG = MID + 1 // end of if // end of loop Step 5: if FLAG = -1 print " element is not found in this list " // end of if Step 6: exit |
For example, suppose you have the following array, and you have to search 30 in it.
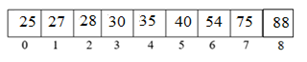
| Iteration 1: BEG = 0 END = 8 MID = (BEG + END) / 2 (0 + 8) / 2 = 4 A[MID] = VAL A[4] = 30 35 ? 30 // not equal Iteration 2: BEG = 0 END = MID – 1 = 4 – 1 = 3 MID = (0 + 3) / 2 = 1 A[1] = VAL 27 ? 30 // not equal Iteration 3: BEG = MID + 1 = 1 + 1 = 2 END = 3 MID = (2 + 3) / 2 = 2 A[2] = VAL 29 ? 30 // not equal Iteration 4: BEG = MID + 1 = 2 + 1 = 3 END = 3 MID = (3 + 3) / 2 = 6 A(3) = VAL 30 = 30 // equal Index value of 32 is 3. |
Binary search program in C language
#include<stdio.h>
int binarySearch(int[], int, int, int);
void main ()
{
int arr[10] = {6, 9, 12, 23, 35, 46, 68, 90, 96, 120};
int item, location=-1;
printf("enter the search element ");
scanf("%d",&item);
location = binarySearch(arr, 0, 9, item);
if(location != -1)
{
printf("element index value is %d",location);
}
else
{
printf("element not found");
}
}
int binarySearch(int a[], int beg, int end, int item)
{
int mid;
if(end >= beg)
{
mid = (beg + end)/2;
if(a[mid] == item)
{
return mid+1;
}
else if(a[mid] < item)
{
return binarySearch(a,mid+1,end,item);
}
else
{
return binarySearch(a,beg,mid-1,item);
}
}
return -1;
}
Output
| enter the search element 35 element index value is 4 |