Heap Sort in Data Structure

Heap Sort

A heap is a tree-based data structure that has specific properties.

• Heap is always a complete binary tree (CBT). That is, all the nodes of the tree are completely filled.
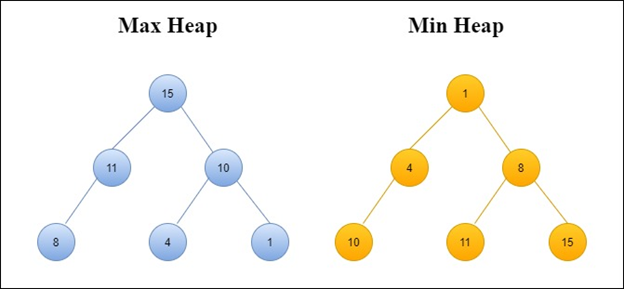
• If the value placed in each node is greater than or equal to its two children, then that heap is called max heap.
• If the value placed in each node is less than or equal to its two children, then that heap is called min-heap.
• If you want to sort the list in ascending order (increasing order), then you create the min-heap.
• If you want to sort the list in descending order (decreasing order), then you create the max heap.

Complexity table of Heap sort

Complexity	Best case	Average case	Worst case
Time	O(nlogn)	O(nlogn)	O(nlogn)
Space			O(1)

Selection sort algorithm

Heapsort (A) 
Build_Max_heap(A)
for i ? length[A] down to 2
do exchange A[i] ? A[1]
heapsize(A) ? heapsize (A – 1)
Max_heapify (A, 1)  

This algorithm is for max heap sort.

Step 1: Create a new node.

Step 2: Assign a value to the node.

Step 3: Compare the value of the child node with the value of the parent node.

Step 4: If the child node value is greater than the parent node value, then interchange them. 

Step 5: Repeat steps 3 and 4 until the heap is sorted correctly.

Build_Max_heap(A)
heapsize(A) ? length[A]
for i ? length[A / 2] down to 1
Max_heapify (A, i)  

Max_heapify (A, i)
 l ? left[i]
r ? right[i]if l <= heapsize(A) and A[l] > A[i]
then largest ? l
also, largest ? iif r <= heapsize(A) and A[r] > A[largest]then largest ? rdo if i ? largestexchange A[i]  ? A[largest]Max_heapify (A, largest)  

Heap sort program in C language

#include<stdio.h>  
int val; 
void heapify(int arr[], int size, int i)
{      
int largest = i;       
int left = 2*i + 1;     
 int right = 2*i + 2;      
  if (left < size && arr[left] >arr[largest])         largest = left;      if (right < size && arr[right] > arr[largest])         largest = right;      if (largest != i)       
 {          
 val = arr[i];          
  arr[i]= arr[largest];        
     arr[largest] = val;         
   heapify(arr, size, largest);       
   }   
}     
 void heapSort(int arr[], int size) 
  {  
      int i;      
  for (i = size / 2 - 1; i >= 0; i--)      
 heapify(arr, size, i);      
  for (i=size-1; i>=0; i--)      
 {           
 val = arr[0];  
          arr[0]= arr[i];      
       arr[i] = val;         
   heapify(arr, i, 0);      
  }  
 }    
  void main() 
  {     
      int arr[] = {20, 50, 40, 10, 90, 80, 60, 70, 30, 100};   
        int i;     
      int size = sizeof(arr)/sizeof(arr[0]);   
       heapSort(arr, size);   
       printf("heap sorted elements\n");  
         for (i=0; i<size; ++i)      
    printf("%d\n",arr[i]);   }    

Output

heap sorted elements
10 
20 
30 
40 
50 
60 
70 
80 
90 
100  

Heap sort program in java language

public class HeapSort      
{       
public void sort(int arr[])       
  {            
int n = arr.length;        // Build max heap         
    for (int i = n / 2 - 1; i >= 0; i--)          
   {          
       heapify(arr, n, i);       
     }                // Heap sort     
 for (int i = n - 1; i >= 0; i--)    
   {       
    int temp = arr[0];    
    arr[0] = arr[i];    
    arr[i] = temp;             // Heapify root element        
 heapify(arr, i, 0);  
     }  
  } 
 void heapify(int arr[], int n, int i)
 {       // Find largest among root, left child and right child             
   int largest = i;     
    int l = 2 * i + 1;    
     int r = 2 * i + 2;   
      if (l < n && arr[l] > arr[largest])    largest = l;      
   if (r < n && arr[r] > arr[largest])   
      largest = r;            // Swap and continue heapifying if root is not largest        
 if (largest != i)      
   {          
  int swap = arr[i];   
         arr[i] = arr[largest];  
          arr[largest] = swap;    
       heapify(arr, n, largest);   
      }
 }              // Function to print an array       
 static void printArray(int arr[])  
        {          
    int n = arr.length;  
            for (int i = 0; i < n; ++i) 
             System.out.print(arr[i] + " ");       
       System.out.println();        
  }            // Driver code   public static void main(String args[]) 
     {      
   int arr[] = { 20, 50, 40, 10, 90, 80, 60, 70, 30, 100 }; 
        HeapSort hs = new HeapSort();     
    hs.sort(arr);     
    System.out.println("heap sorted elements");   
      printArray(arr);   
   } 
}

Output

heap sorted elements 
10
20 
30 
40 
50 
60 
70 
80 
90 
100