Interval Tree
Interval Tree
Interval Tree: The concept is to increase a Binary Search Tree self-balancing such as Red Black Tree, and AVL Tree, so that every feature can be completed in time O(Logn).
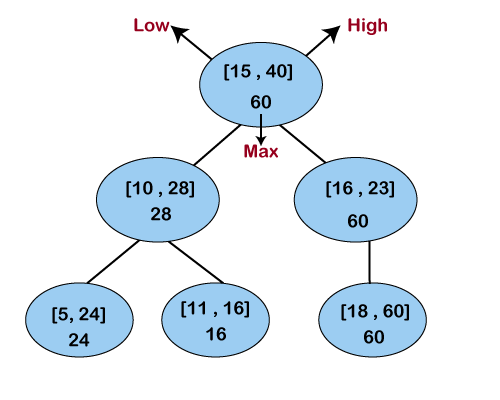
Each Interval Tree node stores information following.
- I: An interval representing a pair [low, high]
- max: Maximum high value in a node-rooted subtree.
The low interval value is used as the key to preserve order within BST.
Insert and delete actions that are used in BST self-balancing are just like insert and delete operations.
The key operation is to search for an interval that overlaps. Following is the new algorithm for an overlapping interval x in a root-rooted Interval tree.
1) If x overlaps with an interval of the root, return interval of the root.
2) If left root child is not empty and the limit in the left child is empty is higher than the low value of x, recur for the child left
3) Similar recurrence for the right child.
Why does the Algorithm above work?
Let the query interval be x. We need to prove this for two cases to follow.
Case 1: One of the following must be valid when we go to the correct subtree.
A) The right subtree overlaps: This is fine, as we need to return one overlapping interval.
B) In either subtree, there is no overlap: we go to the right subtree only if either the left subtree is NULL or the left maximum value is lower than x.low. So, the interval in the left subtree cannot be present.
Case 2: One of the following must be true when we go to the left subtree.
A) The left subtree overlaps: This is fine, as we need to return one overlapping interval.
B) In either subtree, there is no overlap: this is the most important part. We need to consider the facts that follow.
- We went to the left subtree, because in the left subtree x.low <= max
- Max in the left subtree is one of the intervals in the left subtree, let's say [a, max].
- Since x does not overlap with any node in the left x.low subtree, it must be lower than 'a.'
- All nodes in BST are ordered by low value, so the low value of all nodes in the right subtree must be higher than 'a.'
- We can say from the above two facts that all intervals in the right subtree are of a low value greater than x.low. So x in the right subtree cannot overlap with any interval.
C++ establishment of Interval Tree follows. Basic BST insert operation is used to keep it simple in implementation. Ideally, this should be AVL Tree insertion or Red-Black Tree insertion.
#include <iostream>
using namespace std;
// Structure to represent an interval
struct Interval
{
int low, high;
};
// Structure to represent a node in Interval Search Tree
struct ITNode
{
Interval *k; // 'k' could also be a normal variable
int max;
ITNode *left, *right;
};
// A utility function to create a new Interval Search Tree Node
ITNode * newNode(Interval k)
{
ITNode *temp = new ITNode;
temp->k = new Interval(k);
temp->max = k.high;
temp->left = temp->right = NULL;
return temp;
};
ITNode *insert(ITNode *root, Interval k)
{
// Base case: Tree is empty, new node becomes root
if (root == NULL)
return newNode(k);
// Get low value of interval at root
int l = root->k->low;
if (k.low < l)
root->left = insert(root->left, k);
// Else, new node goes to right subtree.
else
root->right = insert(root->right, k);
// Update the max value of this ancestor if needed
if (root->max < k.high)
root->max = k.high;
return root;
}
bool doOVerlap(Interval j1, Interval j2)
{
if (j1.low <= j2.high && j2.low <=j1.high)
return true;
return false;
}
Interval *overlapSearch(ITNode *root, Interval k)
{
// Base Case, tree is empty
if (root == NULL) return NULL;
// If given interval overlaps with root
if (doOVerlap(*(root->k), k))
return root->k;
// If left child of root is present and max of left child is
// greater than or equal to given interval, then i may
// overlap with an interval is left subtree
if (root->left != NULL && root->left->max >= k.low)
return overlapSearch(root->left, k);
// Else interval can only overlap with right subtree
return overlapSearch(root->right, k);
}
void inorder(ITNode *root)
{
if (root == NULL) return;
inorder(root->left);
cout << "[" << root->k->low << ", " << root->k->high << "]"
<< " max = " << root->max << endl;
inorder(root->right);
}
// Driver program to test above functions
int main()
{
// Let us create interval tree shown in above figure
Interval ints[] = {{20, 25}, {15, 60}, {17, 19},
{4, 20}, {13, 15}, {35, 40}
};
int n = sizeof(ints)/sizeof(ints[0]);
ITNode *root = NULL;
for (int t = 0; t < n; t++)
root = insert(root, ints[t]);
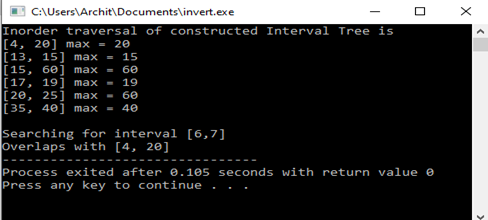
cout << "Inorder traversal of constructed Interval Tree is\n";
inorder(root);
Interval x = {6, 7};
cout << "\nSearching for interval [" << x.low << "," << x.high << "]";
Interval *res = overlapSearch(root, x);
if (res == NULL)
cout << "\nNo Overlapping Interval";
else
cout << "\nOverlaps with [" << res->low << ", " << res->high << "]";
return 0;
}
Output: