Merge Sort

Merge Sort is one of the most widely used sorting algorithms, and it is based on the Divide and Conquer principle.

A problem is subdivided into multiple sub-problems in this method. Each sub-problem is addressed separately. The final solution is formed by combining sub-problems.

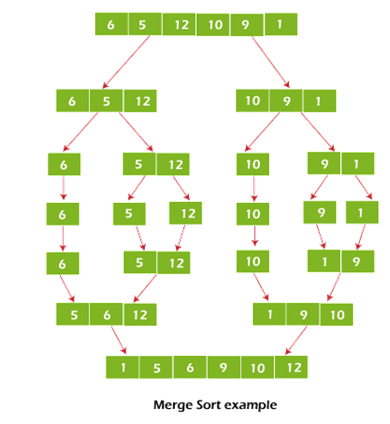
Example of merge sort

Strategy of Divide and Conquer

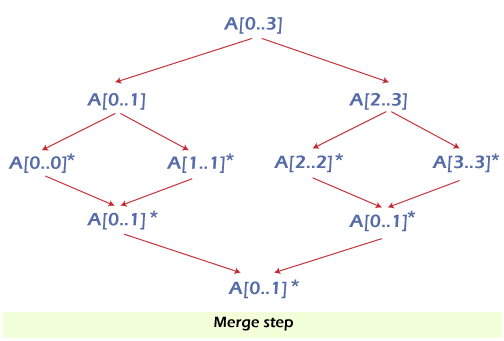
We divide a problem into subproblems using the Divide and Conquer technique. We 'combine' the results from the subproblems to solve the main problem once each subproblem has been solved.

Let's say we needed to sort an array A. Sorting a sub-section of this array starting at index p and ending at index r, denoted as A[p..r], is a subproblem.

Divide

We can split the subarray A[p..r] into two arrays A[p..q] and A[q+1, r] if q is the half-way point between p and r.

Conquer

We try to sort both the subarrays A[p..q] and A[q+1, r] in the conquer step. If we haven't reached the base case yet, we divide both of these subarrays again and try to sort them.

Combine

When the conquer step reaches the base step and we obtain two sorted subarrays A[p..q] and A[q+1, r] for array A[p..r], we combine the results by constructing a sorted array A[p..r] from the two sorted subarrays A[p..q] and A[q+1, r].

Algorithm of Merge Sorting

The MergeSort function divides the array into halves repeatedly until we reach the point where we try to perform MergeSort on a subarray of size one, i.e. p == r.

The merge function then comes into play, combining the sorted arrays into larger arrays until the entire array is merged.

In order to sort an array of n elements in increasing order, use the following commands:

MergeSort(A, p, r):
    if p > r 
        return
    q = (p+r)/2
    mergeSort(A, p, q)
    mergeSort(A, q+1, r)
    merge(A, p, q, r)

To sort an array as a whole, use MergeSort(A, 0, length(A)-1).

The merge sort algorithm recursively splits the data into halves, as shown in the image below, until we reach the base case of an array with one element. The merge function then selects the sorted sub-arrays and merges them to gradually sort the entire array.

How Merge Sort Works?

Assume we're attempting to organise the components ascending.

Every recursive algorithm relies on a base case and the ability to combine results from different base cases. The merge sort is no exception. The merge step, as you might expect, is the most important part of the merge sort algorithm.

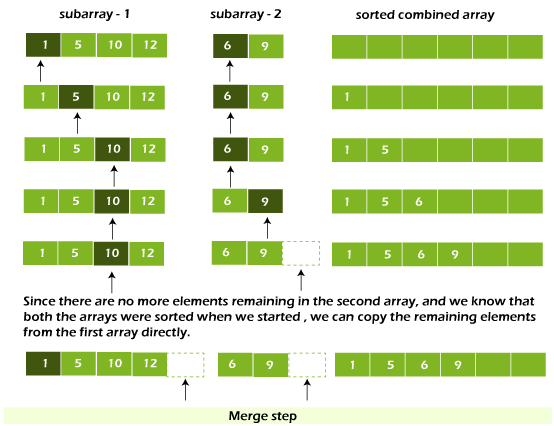
The merge step solves the problem of combining two sorted lists (arrays) into a single large sorted list (array).

The algorithm keeps track of three pointers: one for each of the two arrays and one for the final sorted array's current index.

Have any of the arrays reached their limit?
No:
Both arrays' current elements are compared.
In the sorted array, copy the smaller element.
Move the element's pointer to the smaller element.
Yes:
Copy the non-empty array's remaining elements.

Writing the Merge Algorithm Code

The merge function is only performed on consecutive sub-arrays, which is a noticeable difference between the merging step we described above and the one we use for merge sort.

This is why we only need the array, the first position, the last index of the first subarray (which we can calculate), and the last index of the second subarray.

To create a sorted array A[p..r], we must merge two subarrays A[p..q] and A[q+1..r]. A, p, q, and r are the function's inputs.

This is how the merge function works:

• Make copies of the L A[p..q] and M A[q+1..r] subarrays.
• Make three pointers with the letters I j, and k.
  • I keeps track of the current L index, starting at 1.
  • j keeps track of the current M index, starting at 1.
  • k keeps track of the current A[p..q] index, starting at p.
• Pick the larger of the elements from L and M and place them in the correct position at A[p..q] until we reach the end of either L or M.
• Pick up the remaining elements and place them in A[p..q] when we run out of elements in either L or M.

This would be written in code as:

/ Combine L and M subarrays into arr
void merge(int arr[], int p, int q, int r) {


    // Create L ← A[p..q] and M ← A[q+1..r]
    int n1 = q - p + 1;
    int n2 = r - q;


    int L[n1], M[n2];


    for (int i = 0; i < n1; i++)
        L[i] = arr[p + i];
    for (int j = 0; j < n2; j++)
        M[j] = arr[q + 1 + j];


    // Maintain the current sub-array and main array indexes.
    int i, j, k;
    i = 0;
    j = 0;
    k = p;


    // Pick the larger of the elements L and M and place them in the correct position at A[p..r] until we reach either end of L or M.
    while (i < n1 && j < n2) {
        if (L[i] <= M[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = M[j];
            j++;
        }
        k++;
    }


    // Pick up the remaining elements and place them in A[p..4] when we run out of elements in either L or M. 
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }


    while (j < n2) {
        arr[k] = M[j];
        j++;
        k++;
    }
}

Step-by-Step Explanation of the Merge() Function

This function has a lot going on, so let's look at an example to see how it works.

A picture, as is customary, is worth a thousand words.

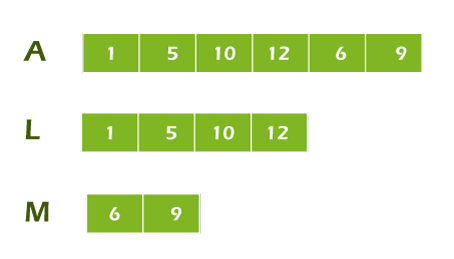
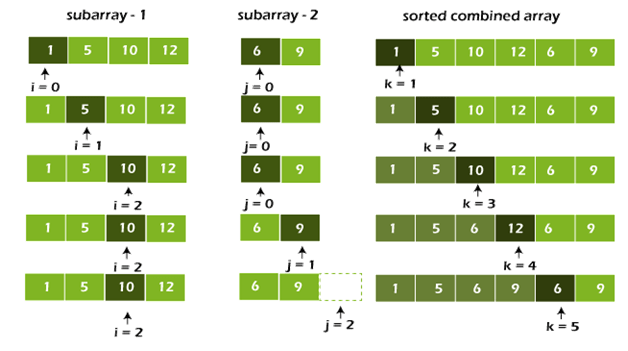
Two sorted subarrays A[0..3] and A[4..5] are contained in the array A[0..5]. Let's take a look at how the merge function combines the two arrays.

void merge(int arr[], int p, int q, int r) {
// Here, p = 0, q = 4, r = 6 (size of array)

Step 1: Make duplicates of the sub-arrays that will be sorted.

// Create L ← A[p..q] and M ← A[q+1..r]
    int n1 = q - p + 1 = 3 - 0 + 1 = 4;
    int n2 = r - q = 5 - 3 = 2;


    int L[4], M[2];


    for (int i = 0; i < 4; i++)
        L[i] = arr[p + i];
        // L[0,1,2,3] = A[0,1,2,3] = [1,5,10,12]


    for (int j = 0; j < 2; j++)
        M[j] = arr[q + 1 + j];
        // M[0,1] = A[4,5] = [6,9]

Step 2: Keep track of the sub-array and main array indexes.

    int i, j, k;
    i = 0; 
    j = 0; 
    k = p; 

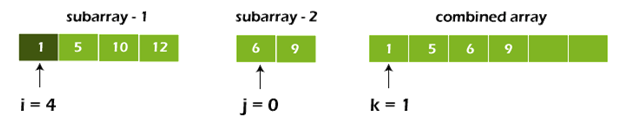
Step 3: Pick the larger of the elements L and M and place them in the correct position at A until we reach the end of either L or M. [p..r]

    while (i < n1 && j < n2) { 
        if (L[i] <= M[j]) { 
            arr[k] = L[i]; i++; 
        } 
        else { 
            arr[k] = M[j]; 
            j++; 
        } 
        k++; 
    }

Step 4: Pick up the remaining elements and place them in A[p..r] when we run out of elements in either L or M

    
 // Because j n2 does not hold, we exited the previous loop.
while (i < n1)
{
    arr[k] = L[i];
    i++;
    k++;
}

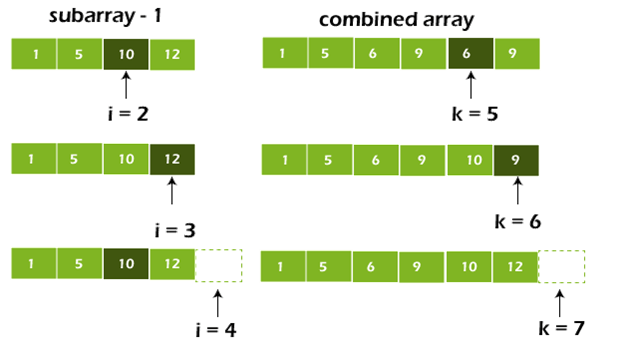
    // Because I < n1 does not hold, so we exited the previous loop.  
    while (j < n2)
    {
        arr[k] = M[j];
        j++;
        k++;
    }
}

If M was larger than L, this step would have been required.

The subarray A[p..r] is sorted at the end of the merge function.

Code for Merge Sort in C

// Merge sort in C


#include <stdio.h>


// Arrange the two subarrays L and M as one.
void merge(int arr[], int p, int q, int r) {


  // Create L ← A[p..q] and M ← A[q+1..r]
  int n1 = q - p + 1;
  int n2 = r - q;


  int L[n1], M[n2];


  for (int i = 0; i < n1; i++)
    L[i] = arr[p + i];
  for (int j = 0; j < n2; j++)
    M[j] = arr[q + 1 + j];


  // Maintain the current sub-array and main array indexes.
  int i, j, k;
  i = 0;
  j = 0;
  k = p;


  //Pick the larger of the elements L and M and place them in the correct position at A[p..r] until we reach either end of L or M.
  while (i < n1 && j < n2) {
    if (L[i] <= M[j]) {
      arr[k] = L[i];
      i++;
    } else {
      arr[k] = M[j];
      j++;
    }
    k++;
  }


  // Pick up the remaining elements and place them in A[p..4] when we run out of elements in either L or M. 
  while (i < n1) {
    arr[k] = L[i];
    i++;
    k++;
  }


  while (j < n2) {
    arr[k] = M[j];
    j++;
    k++;
  }
}


// Divide the array into two subarrays, sort them, and then merge them together.
void mergeSort(int arr[], int l, int r) {
  if (l < r) {


    // m is the intersection of two subarrays in the array.
    int m = l + (r - l) / 2;


    mergeSort(arr, l, m);
    mergeSort(arr, m + 1, r);


    // Merge the sorted subarrays
    merge(arr, l, m, r);
  }
}


// Print the array
void printArray(int arr[], int size) {
  for (int i = 0; i < size; i++)
    printf("%d ", arr[i]);
  printf("\n");
}


// Driver program
int main() {
  int arr[] = {6, 5, 12, 10, 9, 1};
  int size = sizeof(arr) / sizeof(arr[0]);


  mergeSort(arr, 0, size - 1);


  printf("Sorted array: \n");
  printArray(arr, size);
}

The following output should be generated by this programme:

Output

Array Sorted in Ascending Order:
-12 -9 0 17 46

Complexity for Merge Sort

Time Complexity
Best Case	O(n log n)
Worst Case	O(n log n)
Average	O(n log n)
Space Complexity	O(n)
Stability	Yes

Complexities of Time

• Complexity in the worst-case scenario: O (n log n)
• Complexity in the Best-Case Scenario: O (n log n)
• Case Complexity on the Average: O (n log n)

Complexity of Space

Merge sort has a space complexity O (n).

Applications for Merge Sorting

When using the Merge sort,

• Problem with inversion counts.
• Sorting from outside.
• Applications for e-commerce.
• Merge Sort can be used to sort linked lists in O(nLogn) time. The case for linked lists is unique, owing to the differences in memory allocation between arrays and linked lists. Unlike arrays, linked list nodes in memory may not be adjacent. Unlike an array, we can insert items in the middle of a linked list in O(1) extra space and O(1) time. As a result, the merge sort operation can be implemented without the need for additional linked list space.

Merge Sort's Downsides

• For smaller tasks, it is slower than the other sort algorithms.
• For the temporary array, the merge sort algorithm requires an additional memory space of 0(n).
• Even if the array is sorted, it goes through the entire process.