Convex hull Algorithm in C++

The intersection of all convex sets containing a certain subset of a Euclidean space, or alternatively, the set of all convex combinations of points in the subset, defines the convex hull. A rubber band wrapped around a bounded subset of the plane can be used to represent the convex hull as the shape it encloses. The algorithmic concerns of finding the convex hull of a constrained set of points in the plane or other low-dimensional Euclidean spaces, as well as its dual problem of intersecting half-spaces, are fundamental problems in computational geometry. In higher dimensions, they can be solved in a time that corresponds to the worst-case output complexity as stated by the upper limit theorem. They can be solved in time O(nlog n) for two- or three-dimensional point sets. In this article we are going to discuss about convex hull and its algorithm in detail.

What is Convex Hull?

If there are line segments connecting every pair of the points in a set of points in a Euclidean space, the set is said to be convex. The intersection of all half-spaces that contain a set of points S is the convex hull of that set of points. The collection of points on or to one side of a line constitutes a half space in two dimensions. Higher dimensions can be applied to this idea. The group of points on or to one side of a plane constitutes a half-space, and so on. Keep in mind that the convex hull of a set is a closed, "solid" area that contains all of the interior points. Since it is the boundary that we compute and that implies the region, the term is frequently used more loosely in computational geometry to indicate the boundary of this region.

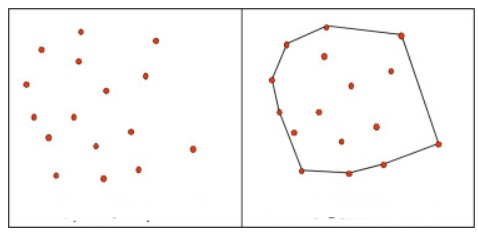
Convex Hull Algorithms

For computing the convex hull of a finite set of points, multiple techniques with varying processing difficulties have been suggested in computational geometry. Constructing a clear and effective representation of the necessary convex shape entails computing the convex hull.

The algorithms are as follows:

1. Chan's algorithm — O(n log h)
2. Divide and conquer — O(n log n)
3. Gift wrapping, a.k.a. Jarvis algorithm — O(nh)
4. Graham scan — O(n log n)
5. Incremental convex hull algorithm — O(n log n)
6. Kirkpatrick–Seidel algorithm — O(n log h)
7. Monotone chain, a.k.a. Andrew's algorithm— O(n log n)
8. Quickhull- O(nlogn)

Algorithm

Jarvis's algorithm's basic concept is that we wrap points counterclockwise, starting with the leftmost point (or the point with the lowest x-coordinate value). Here, using orientation is the idea. The next point is chosen as the point that outperforms all others when oriented counterclockwise, i.e., the following point is q if "orientation(p, q, r) = counterclockwise" is true for any other point r. Make p the leftmost point at startup. The point q that causes the triplet (p, q, r) to rotate counterclockwise for any other point r is the following point. We just initialise q as the next point and then travel through all of the points to discover this. We update q as I for any point I if I is more counterclockwise or if orientation(p, I q) is counterclockwise. The most counterclockwise point will be our final value for q. In the convex output hull, place q after p. For the following iteration, set p to q.

C++ Example:

//CPP program
#include <bits/stdc++.h>
using namespace std;


struct Mypoint
{
	int x, y;
};
int orientation(Mypoint p, Mypoint q, Mypoint r)
{
	int val = (q.y - p.y) * (r.x - q.x) -
			(q.x - p.x) * (r.y - q.y);


	if (val == 0) return 0; 
	return (val > 0)? 1: 2; 
}
void convexHull(Mypoint pointval[], int n)
{
	if (n < 3) return;
	vector<Mypoint> hull;
	int l = 0;
	for (int i = 1; i < n; i++)
		if (pointval[i].x < pointval[l].x)
			l = i;
	int p = l, q;
	do
	{
		hull.push_back(pointval[p]);
		q = (p+1)%n;
		for (int i = 0; i < n; i++)
		{
		if (orientation(pointval[p], pointval[i], pointval[q]) == 2)
			q = i;
		}
		p = q;


	} while (p != l); 
	for (int i = 0; i < hull.size(); i++)
		cout << "(" << hull[i].x << ", "
			<< hull[i].y << ")\n";
}
int main()
{
	Mypoint pointval[] = {{1, 3}, {1, 2}, {4, 1}, {2, 5},
					{3, 1}, {2, 0}, {3, 2}};
	int n = sizeof(pointval)/sizeof(pointval[0]);
	convexHull(pointval, n);
	return 0;
}


//JAVA program
import java.util.*;


class Mypoint
{
	int x, y;
	Mypoint(int x, int y){
		this.x=x;
		this.y=y;
	}
}


class bn {
	
	public static int orientation(Mypoint p, Mypoint q, Mypoint r)
	{
		int val = (q.y - p.y) * (r.x - q.x) -
				(q.x - p.x) * (r.y - q.y);
	
		if (val == 0) return 0; 
		return (val > 0)? 1: 2; 
	}
	
	public static void convexHull(Mypoint pointval[], int n)
	{
		if (n < 3) return;
		Vector<Mypoint> hull = new Vector<Mypoint>();
	
		int l = 0;
		for (int i = 1; i < n; i++)
			if (pointval[i].x < pointval[l].x)
				l = i;
	
		int p = l, q;
		do
		{
			hull.add(pointval[p]);
	
			q = (p + 1) % n;
			
			for (int i = 0; i < n; i++)
			{
			if (orientation(pointval[p], pointval[i], pointval[q])
												== 2)
				q = i;
			}
	
			p = q;
	
		} while (p != l); 
	
		for (Mypoint temp : hull)
			System.out.println("(" + temp.x + ", " +
								temp.y + ")");
	}
	
	public static void main(String[] args)
	{


		Mypoint pointval[] = new Mypoint[7];
		pointval[0]=new Mypoint(0, 3);
		pointval[1]=new Mypoint(2, 3);
		pointval[2]=new Mypoint(1, 1);
		pointval[3]=new Mypoint(2, 1);
		pointval[4]=new Mypoint(3, 0);
		pointval[5]=new Mypoint(0, 0);
		pointval[6]=new Mypoint(3, 3);
		
		int n = pointval.length;
		convexHull(pointval, n);
		
	}
}

Output: