Backtracking Time Complexity in C++
Introduction to Backtracking
Backtracking is an important part of programming languages, and with the help of backtracking, we can do many operations in an advanced data structure. For doing major operations, we need backtracking. If we simplify backtracking, that means finding all possible solutions and using the one you want.
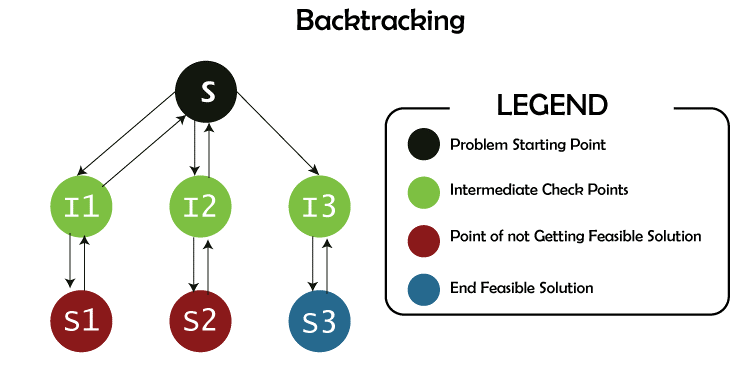
Backtracking Time Complexity
Backtracking is one of the problem-solving strategies. Using this approach, we can solve problems and write our algorithm by following this strategy. This strategy is used by brute – force approach.
Why is the time complexity of backtracking exponential?
When you talk about time complexity, you are talking about the worst case; in a backtracking algorithm, you traverse every path.
Traversing every path in a graph takes an exponential amount of time.
Assuming there are 100 nodes and from each node there are two paths, then you traverse 2^100 paths, i.e., about 10^30, which is huge and exponential.
The time complexity of backtracking shows how many times the function calls itself.
If the function calls itself three times, its time complexity is o(3^N), and if it calls five times, the o(5^N). The complexity of backtracking can be defined as o(k^N), where k shows how many numbers of time function call itself.
Explanation About Backtracking
Backtracking is like a divide-and-conquer technique in dynamic programming and a greedy approach. Now we have a question: why do we require backtracking when having a divide-and-conquer greedy technique approach and dynamic programming? If we compare backtracking with dynamic programming, the purpose of dynamic programming is to find an optimal solution, but in backtracking, we don't want only one optimal solution; we need to work on more than one solution.
Now, as the name suggests, backtracking means when we cannot find any solution, so that time we should start backtracking; we traverse each node from bottom to top hence called backtracking. We can say backtracking Is the brute–force method. It is a method where we should check all possibilities, but there is a minor difference between backtracking and brute force.
What is the difference between Backtracking and Brute Force
Both of them look very similar, but the main difference is that:
- In brute force: you generate all the possible conditions you can, and then you check if any of them is the answer you want
- In backtracking: You check if this step satisfies all the conditions in each step. If it does: you continue generating subsequent solutions. If not: you go one step backward to check for another path.
Is Recursion called backtracking?
Recursion is a technique where we a function calls itself like a cycle until we reach the base case. Backtracking is an algorithm or an approach that finds a possible solution and chooses the required solution from the given set of solution.
Backtracking program using Recursion in Java
public class Recursion3 {
public static void printPermutation(String str, int idx, String perm) {
if(str.length() == 0) {
System.out.println(perm);
return;
}
for(int i=0; i<str.length(); i++) {
char currChar = str.charAt(i);
String newStr = str.substring(0, i) + str.substring(i+1);
printPermutation(newStr, idx+1, perm+currChar);
}
}
public static void main(String args[]) {
String str = "abc";
printPermutation(str, 0, "");
}
}
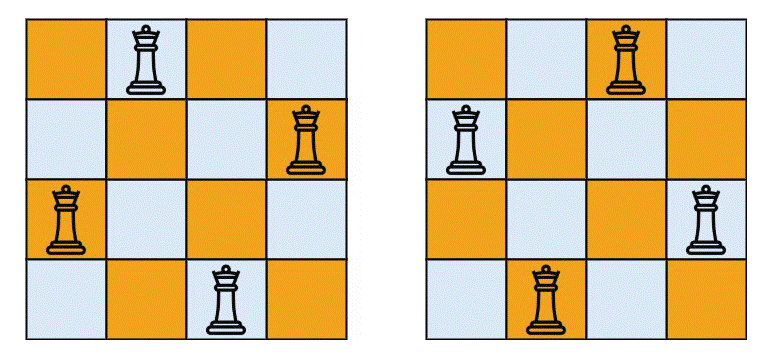
N Queen Problem: An Example of Backtracking
There is an example of Backtracking, which is N-queen Problem. Here the question gives a 5/5 chess board means five rows and five columns. For a 5/5 chessboard, we have five queens, so we need to print all solutions where queens are safe.
what happens on the top of the chessboard is that each piece can be cut and removed from the chessboard. Each player has different ways of playing, so the queen also has a way of cutting each piece, so how can all be played? We have to print all possible combinations so that they are safe and no one can cut them.
So let's discuss how we will solve this problem. We have four queens Q1, Q2, Q3 Q4. These four we have to place on a 4/4 chess board, so our approach will be like this we will place the first queen to first column somewhere, and accordingly, we will try to place the second queen in the next column and then try to place its next queen in the third column. Now, why are we placing one queen in one column? Placing one queen in one column means placing only one queen in this entire line because in any of these positions if one queen is placed on that side, The queen can kill all the queens, so there can be only one queen in a column.
So our approach was to go column-wise and place one queen in each column. Where the first one is placed, after the next one is placed, and each time before placing the queen, we will check where we have placed the queen. Whether that place is safe or not, or how will we check that there is no other queen in all the eight directions of that queen? If a queen is placed, it is not right to place that queen, will backtrack.