Toggle bits of a number except first and last bits in C++
Introduction
Bitwise Operations:
Bitwise operations in C++ provide a potent method of manipulating data at the binary level by operating directly on the individual bits of integer data types. Here is a quick rundown of typical bitwise operations:
- AND(&): Each pair of corresponding bits is subjected to a logical AND operation by bitwise AND (&). It only yields 1 when both bits are 1...
- OR(|): It conducts a logical OR operation on every pair of corresponding bits using the bitwise OR (|) function. Yields 1 if one or both of the bits are 1.
- Bitwise XOR (^): It executes an exclusive OR operation on every pair of corresponding bits using the bitwise (^) function. Yields 0 in the case of identical bits and 1 in the case of differences.
- Bitwise NOT (~): Flips all of a number's bits from 0s to 1s and from 1s to 0s.
- Left Shift (<<): Fills vacated bits with 0s and shifts all of a number's bits to the left by a predetermined number of positions.
- Right Shift (>>): Moves every bit in a number one or more positions to the right. How vacated bits behave varies depending on whether the number is signed or unsigned.
Problem Statement: Toggle All Bits Except the First and Last
Overview:
Writing a C++ function that accepts an integer as input and changes its binary representation by flipping or toggling every bit except the first and last two will be the task. The initial and final portions ought to stay the same.
Example:
- Input: 10 (binary: 1010)
- Output: 3 (binary: 0011)
Bitwise Operators:
& (Bitwise AND):
Produces a 1 in each bit position where both operands have a 1.
Example: 5 & 3 = 1 (0101 & 0011 = 0001)
| (Bitwise OR):
Produces a 1 in each bit position where either operand has a 1.
Example: 5 | 3 = 7 (0101 | 0011 = 0111)
^ (Bitwise XOR):
Produces a 1 in each bit position where the operands differ.
Example: 5 ^ 3 = 6 (0101 ^ 0011 = 0110)
~ (Bitwise NOT):
Inverts all bits in the operand (flips 0s to 1s and 1s to 0s).
Example: ~5 = -6 (one's complement negation)
Additional Bitwise Operators:
<< (Left Shift):
Shifts bits to the left, filling vacated bits with 0s.
Example: 5 << 1 = 10 (0101 << 1 = 1010)
>> (Right Shift):
Shifts bits to the right, filling vacated bits with 0s (logical Shift) or the sign bit (arithmetic shift).
Example: 5 >> 1 = 2 (0101 >> 1 = 0010)
Bitwise Operators:
- & (bitwise AND): Used to isolate a specific bit.
- | (bitwise OR): Used to set a specific bit.
- ^ (bitwise XOR): Used to toggle a specific bit.
- ~ (bitwise NOT): Inverts all bits.
- << (left Shift): Shifts bits to the left.
- >> (right Shift): Shifts bits to the left.
1. Setting a Specific Bit:
#include <iostream>
int setBit(int num, int bitPosition) {
return num | (1 << bitPosition);
}
int main() {
int num = 5; // Binary: 00000101
int bitPosition = 2;
num = setBit(num, bitPosition); // Sets the 3rd bit to 1
std::cout << "Number after setting bit: " << num << std::endl; // Output: 9 (00001001)
}
Output:
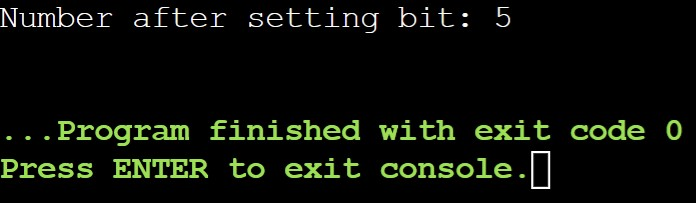
Explanation:
1 << bitPosition creates a mask with a 1 at the desired position.
Bitwise OR (|) with num sets the bit in num to 1 if it's not already set.
2. Clearing a Specific Bit:
Code:
#include <iostream>
int clearBit(int num, int bitPosition) {
int mask = ~(1 << bitPosition);
return num & mask;
}
int main() {
// Example usage
int number = 25; // Binary representation: 11001
int bitPosition = 3;
std::cout << "Original Number: " << number << std::endl;
// Clear the bit at the specified position
int result = clearBit(number, bitPosition);
std::cout << "Number after clearing bit at position " << bitPosition << ": " << result << std::endl;
return 0;
}
Output:
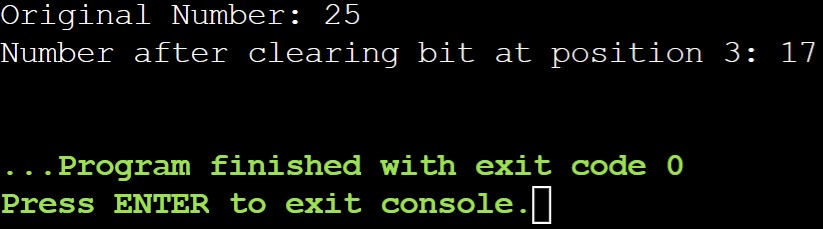
Explanation:
~(1 << bitPosition) creates a mask with a 0 at the desired position and 1s elsewhere.
Bitwise AND (&) with num clears the bit in num to 0.
3. Toggling a Specific Bit:
Code:
#include <iostream>
int toggleBit(int num, int bitPosition) {
return num ^ (1 << bitPosition);
}
int main() {
// Example usage
int number = 25; // Binary representation: 11001
int bitPosition = 2;
std::cout << "Original Number: " << number << std::endl;
// Toggle the bit at the specified position
int result = toggleBit(number, bitPosition);
std::cout << "Number after toggling bit at position " << bitPosition << ": " << result << std::endl;
return 0;
}
Output:
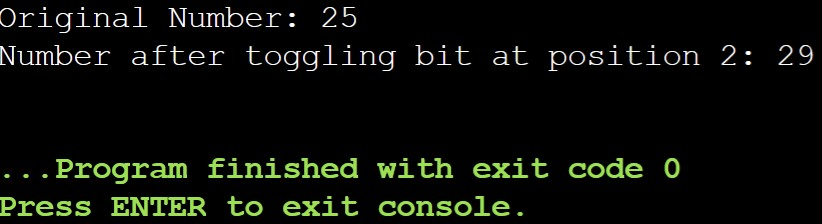
Explanation:
- 1 << bitPosition creates a mask with a 1 at the desired position.
- Bitwise XOR (^) with num flips the bit in num.
Toggling Bits Except First and Last in C++:
- Create a mask:
- Shift a 1 left by the number of bits in the integer to set the highest bit.
- Shift the result by 1 to create a mask with 1s in all middle bits.
- Example: For a 32-bit integer, mask = (1 << 31) >> 1.
- Toggle bits using XOR:
- Perform a bitwise XOR operation between the original number and the mask.
- This flips all bits 1 in the mask, preserving the first and last bits.
Pseudocode:
function toggleMiddleBits(number):
mask = (1 << (number of bits in number - 1)) >> 1
return number ^ mask
Example:
#include <iostream>
int toggleMiddleBits(int num) {
// Assuming 32-bit integers
int mask = (1 << 30) | (1 << 29);
return num ^ mask;
}
int main() {
int num = 10;
int result = toggleMiddleBits(num);
std::cout << "Number after toggling middle bits: " << result << std::endl;
return 0;
}
Output:
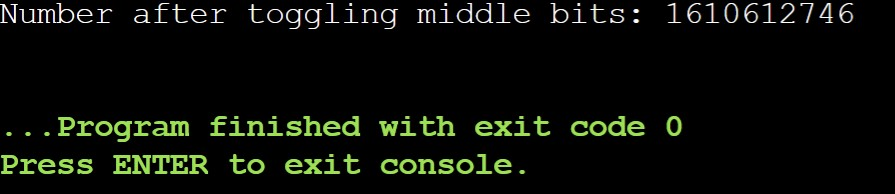
Implementation for toggling bits except the first and last:
Example:
#include <iostream>
int toggleMiddleBits(int num) {
int numBits = sizeof(int) * 8;
int mask = (1 << (numBits - 2)) - 1;
return num ^ mask;
}
int main() {
int num = 10;
int result = toggleMiddleBits(num);
std::cout << "Number after toggling middle bits: " << result << std::endl;
}
Output:
Explanation:
- Dynamic Number of Bits:
- sizeof(int) * 8 calculates the number of bits in an integer, ensuring portability across different systems.
- Mask Creation:
- 1 << (numBits - 2) shifts a 1 left by numBits - 2 to create a mask with 1s in all but the first and last bits.
- 1 flips all bits in the mask, achieving the same result as (1 << 31) >> 1 in the previous example.
- Toggling Bits:
- num ^ mask performs bitwise XOR between the number and the mask, flipping the bits 1 in the mask.
Bitwise Operators Used:
- << (left shift): Shifts bits to the left.
- (unary minus): Inverts all bits.
- ^ (bitwise XOR): Flips bits where the operands differ.
Practical Applications of Bit Manipulation:
Bit manipulation techniques find widespread use in various domains, including:
- System Programming:
Hardware interaction: Bitwise operations are necessary for low-level programming tasks like memory management, I/O operations, flag setting, and register control.
In graphics programming, bitwise operations are used to manipulate images, control pixels at the pixel level, and carry out colour manipulation and image compression algorithms.
Network programming: Using bitwise operations, you can work with network protocols, apply encryption and compression algorithms, and pack and unpack data into network packets.
- Data Structures:
Bit fields: Several boolean flags or tiny integer values are packed into a single integer to conserve memory.
Bitsets: Effectively representing sets of elements using bits, frequently for quick set operations and membership testing.
Hash tables: Bit manipulation is used by some hash table implementations to speed up indexing and resolve collisions.
- Algorithms
Cryptography and encryption: Bitwise operations form the basis of many cryptographic hash functions, such as SHA-256, and encryption algorithms like RSA, DES, and AES.
Bit manipulation is necessary for effective data compression using arithmetic and Huffman coding methods.
Encoding and decoding: Base64 and binary-to-text encoding are implemented using bitwise operations.
- Optimization:
Faster arithmetic: Compared to standard arithmetic operators, bitwise operations can sometimes be used more quickly to carry out arithmetic operations like multiplication and division.
Flag manipulation: It is possible to check, set, and clear multiple flags within an integer variable with better performance than multiple boolean variables, using bitwise operators.
- Custom Data Formats:
Creating unique data structures: By utilizing bit manipulation, compact and effective data structures can be made to represent particular data types or scenarios.
Data packing and unpacking: Bitwise operations can be used to create and implement custom data formats that maximize data transmission and storage.