Skyline Problem in C++

We have given n rectangular buildings in a 2-dimensional city. Here, to compute the Skyline of the given n rectangle structures in a two-dimensional metropolis while removing hidden lines, the primary job is to delete all portions of systems that are not visible after viewing them from a distance.

A triplet represents each building, and all structures have a standard bottom (left, ht, right)

• Left: Is the left side of x coordinated(or wall)?
• Right: The right side's x coordinate.
• Ht: The building's height is indicated by ht.

An urban skyline is made up of many rectangular strips. A pair (left, ht) is used to describe a rectangular strip, where left denotes the x coordinate of the strip's left side and its height.

Example:

Buildings[][] = 1, 11, 5, 2, 6, 7, 9, 12, 14, 3, 25, 19, 18, 22, 23, 13, 29, 24, and 4 (in that order)

Output: 1, 11, 3, 13, 9, 0; 12, 7; 16, 3; 19, 18; 22, 3; 23, 13; 29, 0;

Approach:

• Retrieve the left wall location, height, and correct wall location values for each structure from the triplets provided.
• Keep the pair of the right wall's total height, and the left wall's negative height value in a vector called walls. This is done to distinguish between the left and right borders of the same building.
• Order the walls from highest to lowest.
• Cross the vector walls, and if a left wall is discovered, put its height in the multiset M. If a suitable barrier is met in any other case, take the multiset's appropriate height out.
• Verify whether the top value has changed. Update the maximum value and save the current wall's abscissa if it has changed (x-coordinate).
• The value pairs kept in the skyline vector should be printed.

Example:

// C++ programme for themethod described above
#include <bits/stdc++.h>
usingnamespace std;
// work to construct a skyline
vector<pair<int, int>>
create skylines(vector<vector<int>>& buildings)
{
 
    // learn how manybuildings there are.
    int N = buildings.size();
 
    // To keep track of the buildings' left and right wall positions.
    vector<pair<int, int>> wall;
 
    // triplet of architectural elements and parameters
    int left, height, right;
    for (inti = 0; i< N; i++) {
 
        // veer to the left of the building
        left = buildings[i][0];
 
        // veer to the left of the building
        height = buildings[i][1];
 
        // the appropriate building location
        right = buildings[i][2];
 
        // Keep left point and height in mind.
        // from the left wall.
        // Negative value indicates the left wall.
        // first be added into the multiset
        // identical abscissa(x) as the right wall
        wall.push_back({ left, -height });
 
        // Store the right wall's correct point and height.
        wall.push_back(
            make_pair(right, height));
    }
 
    // order the walls from highest to lowest
    sort(wall.begin(), wall.end());
 
    // output storing Skyline
    vector<pair<int, int>> skyline;
 
    // Begin a multiset with
    // Organize the heights of the left wall.
    multiset<int>leftWallHeight = { 0 };
 
    // Maximum height currently among leftWallHeights
    int top = 0;
 
    // Through the sorted walls, turn.
    For (autow wall) {
 
        // if one finds the left wall
        if (w.second< 0) {
 
            // Add the height.
            left all eight.insert(-w.second);
        }
 
        // if one finds the right wall
        else {
 
            // Take the height down
            left all eight.erase(
                left all eight.find(w.second));
        }
        //.rbegin(): Mark a skyline point if the top changes. backward iteration
 
        if (*leftWallHeight.rbegin() != top) {
 
            top = *leftWallHeight.rbegin();
            skyline.push_back(
                make_pair(w.first, top));
        }
    }
    //Skyline to print again Skyline
    return Skyline;
}
   // Print the output skyline using this function.
voidprint skyline(
    vector<vector<int>>& buildings)
{
 
      // Skyline creation function call
    vector<pair<int, int>> skyline
        = create skylines(buildings);
 
    cout<< "Skyline for the given."
         << " buildings:\n{";
 
    for (autoit: skyline) {
 
        cout<< "{" <<it.first<< ", "
             <<it.second<< "} ";
    }
    cout<< "}";
}
//Driver Number
 int main()
{
    vector<vector<int>> buildings;
    //Given the wall's height and the left and right locations,
    buildings = { { 1, 11, 5 }, { 2, 6, 7 },
                  { 3, 13, 9 }, { 12, 7, 16 },
                  { 14, 3, 25 }, { 19, 18, 22 },
                  { 23, 13, 29 }, { 24, 4, 28 } };
   //Feature Call
    print skyline(buildings);
    return 0;
}

Output:

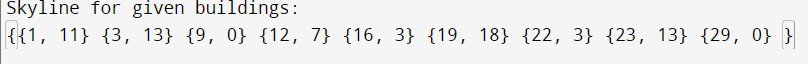
Time Complexity: O(n*log(N))

Auxiliary Space: O(N)