Minimum Cost Path Problem in C++
This article will clarify the concept of the Minimum Cost Path Problem in C++ using Solutions with easy-to-understand examples. The Minimum Cost Path Problem is a decision-based problem to find the least total cost. In this problem, there is a matrix, and we return the minimum cost from the starting point to the end. Basically, these problem-based questions are asked in many interviews and by some popular online coding platforms like Leetcode, HackerRank, etc.
Minimum Cost Path Problem
Suppose we have a matrix and all the cells have a cost associated with it. After that, we have to return the minimum cost of reaching the destination cell (n-1, m-1) from the starting cell (0,0). From each cell, we can only traverse:
- 1 cell to the right side
- 1 cell to the downside
- 1 cell diagonally
Suppose, here is a cell given (i, j), cells (i+1, j), (i, j+1), and (i+1, j+1) can be traversed.
Problem
Here is given a 2D array of dimensions m x n. Each cell of the matrix has a cost. And we have to evaluate the minimum cost by reaching the last cell. i.e. cell with index (m-1) x (n-1) from the first cell i.e. (0) x (0) index.

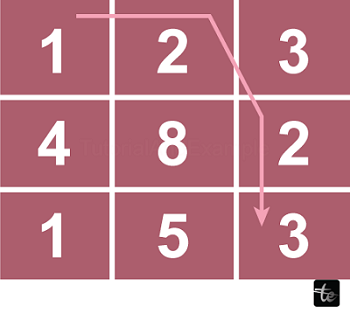
The matrix path with minimum cost is shown in the following figure. Here is the path: (0, 0) >> (0, 1) >> (1, 2) >> (2, 2). The minimum total cost of the path is 8 (1 + 2 + 2 + 3).
After getting the minimum cost path of a given matrix, now we will try to solve the same problem using Recursion.
Min Cost Path Problem Solving Using Recursion
Consider the given suggestions to solve the given problem:
- This query contains the optimal substructure property. Here the path to access (m, n) must be passed over by one of the 3 cells: (p-1, q-1) or (p-1, q) or (p, q-1).
- Therefore, the minimum cost to reach the destination (p, q) can be denoted as min of the 3 cells + cost[p][q].
- MinCost(p, q) = min (MinCost(p-1, q-1), MinCost(p-1, q), MinCost(p, q-1)) + cost[m][n].
Now, follow the given below steps to solve the given query:
- If q and p is less than zero, then return Integer Maximum.
- If p and q is equal to zero, then return cost[p][q].
- Return cost[p][q] + minimum of (MinCost(p-1, q-1), MinCost(p-1, q), MinCost(p, q-1)).
Below is the code in C++ for the above implementing ideas:
#include <bits/stdc++.h>
using namespace std;
#define P 3
#define Q 3
int min(int x, int y, int z);
int minCost(int cost[P][Q], int p, int q)
{
if (q < 0 || p < 0)
return INT_MAX;
else if (p==0 && q==0)
return cost[p][q];
else
return cost[p][q]
+ min(minCost(cost, p - 1, q - 1),
minCost(cost, p - 1, q),
minCost(cost, p, q - 1));
}
int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
int main()
{
int cost[P][Q]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
cout << minCost(cost, 2, 2) << endl;
return 0;
}
Output:

Time Complexity: O((p*q)3
Auxiliary Space: O(p+q)
Now, move to discuss another popular method to solve min cost path problems with a C++ example.
Min Cost Path Using Memoization
The recursive method is not enough for large values. Also, its time complexity is exponential with the number of turns (i.e. time complexity O(2N).- Using the recursive function, we can recompute the same thing multiple times. On the other side, the Memoization method saves the results of the sub-problems into a table. The recursive method can do only up to N=24. Here is a dynamic programming-based solution for the MCP problem.
#include <bits/stdc++.h>
using namespace std;
#define P 3
#define Q 3
int min(int a, int b, int c);
int minCostMemoized(int cost[P][Q], int p, int q,
int memo[P][Q])
{
if (q < 0 || p < 0)
return INT_MAX;
else if (p == 0 && q == 0)
return cost[p][q];
if (memo[p][q] != -1)
return memo[p][q];
memo[p][q]
= cost[p][q]
+ min(minCostMemoized(cost, p - 1, q - 1, memo),
minCostMemoized(cost, p - 1, q, memo),
minCostMemoized(cost, p, q - 1, memo));
return memo[p][q];
}
int minCost(int cost[P][Q], int p, int q)
{
int memo[P][Q];
memset(memo, -1,
sizeof(memo));
return minCostMemoized(cost, p, q, memo);
}
int min(int a, int b, int c)
{
if (a < b)
return (a< c) ? a : c;
else
return (b < c) ? b : c;
}
int main()
{
int cost[P][Q]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
cout << minCost(cost, 2, 2) << endl;
return 0;
}
Output:
