Precision of floating point numbers Using these functions floor(), ceil(), trunc(), round() and setprecision() in C++
Precision of floating point numbers Using these functions floor(), ceil(), trunc(), round() and setprecision() in C++
1/2 decimal equal is 0.555555555555555555555 .... An indefinite number of lengths will require the storage of infinite memory, and we usually have 4 or 8 bytes. Floating point numbers thus only store a certain number of important numbers, and the remainder is missing. The accuracy of a floating-point number describes how often significant digits without loss of data it can show. Cout has a standard precision of 6 when extracting floating point, and serializes everything after.
There are few library and methods given below which are used to produce C++ floating point with precision:
ceil():
The ceil() rounds off of the value given to the nearest integer and more than the amount determined.
Example:
// C++ program to demonstrate working of ceil()
// in C/C++
#include<bits/stdc++.h>
using namespace std;
int main()
{
double a = 2.411, b = 2.500, c = 2.611;
cout << ceil(a) << endl;
cout << ceil(b) << endl;
cout << ceil(c) << endl;
double x1 = -4.411, y1 = -4.500, z1 = -4.611;
cout << ceil(x1) << endl;
cout << ceil(y1) << endl;
cout << ceil(z1) << endl;
return 0;
}
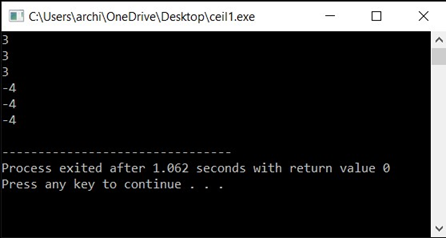
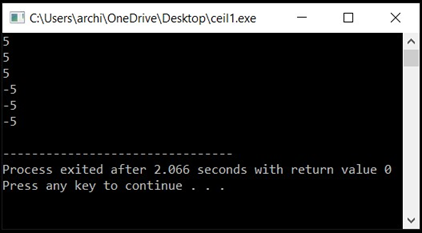
Output:
floor():
Floor rounds the specific value down to the nearest integer that is less than the specific amount.
Example:
/* C++ program to illustrate floor() function in C++*/
#include<bits/stdc++.h>
using namespace std;
int main()
{
double x0 =3.411, y0 =3.500, z0 =3.711;
cout << floor(x0) << endl;
cout << floor(y0) << endl;
cout << floor(z0) << endl;
double i01 =-3.411, j02 =-3.500, k03 =-3.611;
cout << floor(i01) << endl;
cout << floor(j02) << endl;
cout << floor(k03) << endl;
return 0;
}
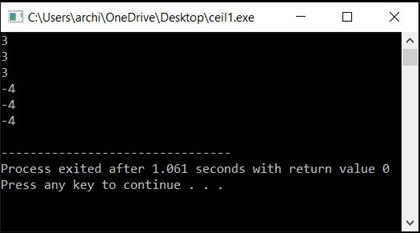
Output:
round():
Rounds with numbers provided to the nearest integer.
Example:
// C++ program to demonstrate working of round()
// in C/C++
#include<bits/stdc++.h>
using namespace std;
int main()
{
double p1 = 4.411, p2 = 4.500, p3 = 4.611;
cout << round(p1) << endl;
cout << round(p2) << endl;
cout << round(p3) << endl;
double x1 = -4.411, x2 = -4.500, x3 = -4.611;
cout << round(x1) << endl;
cout << round(x2) << endl;
cout << round(x3) << endl;
return 0;
}
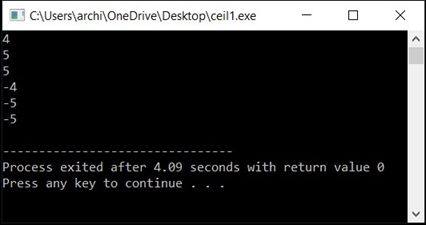
Output:
trunc():
After decimal place, Trunc rounds erase digit numbers.
Example:
// C++ program to demonstrate working of trunc()
// in C/C++
#include<bits/stdc++.h>
using namespace std;
int main()
{
double y01 = 5.411, y02 = 5.500, y03 = 5.611;
cout << trunc(y01) << endl;
cout << trunc(y02) << endl;
cout << trunc(y03) <<endl;
double s01 = -5.411, s02 = -5.500, s03 = -5.611;
cout << trunc(s01) <<endl;
cout << trunc(s02) <<endl;
cout << trunc(s03) <<endl;
return 0;
}
Output:
setprecision():
Especially when combined with 'fixed' set precision provides correct floating-point numbers to decimal numbers provided in setprecision brackets.
Example:
// C++ program to demonstrate working of setprecision()
// in C/C++
#include<bits/stdc++.h>
using namespace std;
int main()
{
double pi = 4.14159, npi = -4.14159;
cout << fixed << setprecision(0) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(1) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(2) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(3) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(4) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(5) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(6) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(7) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(8) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(9) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(10) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(11) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(12) << pi <<" "<<npi<<endl;
cout << fixed << setprecision(13) << pi <<" "<<npi<<endl;
}
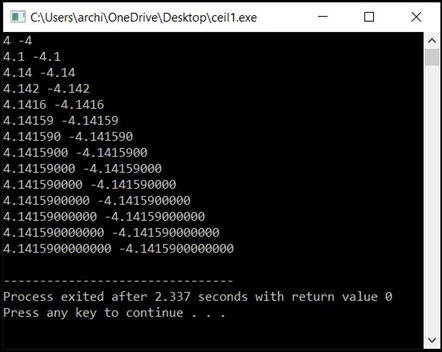
Output: