C++ Deque
Definition:
Deque or the Doubly ended queue is a data structure or operation performed under queue where insertion and deletion are allowed at both ends.
A deque is an ordered collection of items similar to that of a queue. It has a front, a rear and the items can be positioned from both ends allowing it to provide a hybrid linear structure with all the capabilities of stacks and queues in a single frame.
There are various operations performed on deque. The four common operations are:
- insertFront(): Front item is added in the deque.
- insertLast(): Rear item is added in the deque.
- deleteFront(): It deletes the first item from the deque.
- deleteLast(): It deletes the last rear item from the deque.
There are still many additional functions associated with the deque. Some of them are listed below.
- getFront(): Fetches the first item from the deque.
- getRear(): Fethes the last item from the deque.
- isEmpty(): Checks for empty or existence.
- isFull(): Checks whether the deque is full or not.
Let us now move forward with the implementation of the deque.
Deque is most commonly implemented using a doubly linked-list or a circular array. One advantage of this implementation is that both implementations take O(1) complexity.
Let us see coding examples to visualize the implementation techniques.
Example 1: Using Circular Array
#include<bits/stdc++.h>
using namespace std;
#define MAX 100
class Deque
{
int arr[MAX];
int front;
int rear;
int size;
public :
Deque(int size)
{
front = -1;
rear = 0;
this->size = size;
}
void insertfront(int key);
void insertrear(int key);
void deletefront();
void deleterear();
bool isFull();
bool isEmpty();
int getFront();
int getRear();
};
bool Deque::isFull()
{
return ((front == 0 && rear == size-1)||
front == rear+1);
}
bool Deque::isEmpty ()
{
return (front == -1);
}
void Deque::insertfront(int key)
{
if (isFull())
{
cout << "Overflow condition\n" << endl;
return;
}
if (front == -1)
{
front = 0;
rear = 0;
}
else if (front == 0)
front = size - 1 ;
front = front-1;
arr[front] = key ;
}
void Deque ::insertrear(int key)
{
if (isFull())
{
cout << " Overflow\n " << endl;
return;
}
if (front == -1)
{
front = 0;
rear = 0;
}
else if (rear == size-1)
rear = 0;
else
rear = rear+1;
arr[rear] = key ;
}
void Deque ::deletefront()
{
if (isEmpty())
{
cout << "Queue Underflow\n" << endl;
return ;
}
if (front == rear)
{
front = -1;
rear = -1;
}
else
if (front == size -1)
front = 0;
else
front = front+1;
}
void Deque::deleterear()
{
if (isEmpty())
{
cout << " Underflow\n" << endl ;
return ;
}
if (front == rear)
{
front = -1;
rear = -1;
}
else if (rear == 0)
rear = size-1;
else
rear = rear-1;
}
int Deque::getFront()
{
if (isEmpty())
{
cout << " Underflow\n" << endl;
return -1 ;
}
return arr[front];
}
int Deque::getRear()
{
if(isEmpty() || rear < 0)
{
cout << " Underflow\n" << endl;
return -1 ;
}
return arr[rear];
}
int main()
{
Deque dq(5);
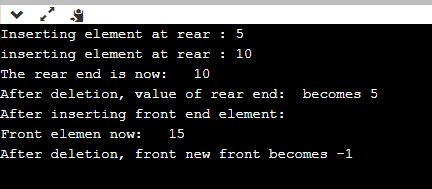
cout << "Inserting element at rear : 5 \n";
dq.insertrear(5);
cout << "inserting element at rear : 10 \n";
dq.insertrear(10);
cout << "The rear end is now: " << " "
<< dq.getRear() << endl;
dq.deleterear();
cout << "After deletion, value of rear end: "
<< " becomes " << dq.getRear() << endl;
cout << "After inserting front end element: \n";
dq.insertfront(15);
cout << "Front elemen now: " << " "
<< dq.getFront() << endl;
dq.deletefront();
cout << "After deletion, front new "
<< "front becomes " << dq.getFront() << endl;
return 0;
}
Output:
Explanation:
The above code is an implementation of deque using the circular array. The following steps are followed:
Algorithm:
- Construct array 'arr' of size 'n'
Assign front = -1 , rear = 0
Inserting value in rear and front means the same in the deque.
After insertion operation:
Front = 0 and Rear = 0
Now, insert rear elements.
a). Check queue is full or not
b). IF Rear == Size-1
Assign rear= 0 ;
Assign rear=rear+1;
Insert or push rear into Arr[ rear ] = key
The front remains the same.
- Inserting front element
a). Check if the deque is full or not.
b). IF Front == 0 or at starting position
OR
The front element points to the last, then
front = size - 1
Else
Decrement front by 1 and push the array.
The rear remains the same.
- Delete Element From Rear end :
a). first Check deque is Empty or Not
b). If there is only one element in the deque
Assign front = -1 ; rear =-1 ;
Else
Check if the front points to the last index or not.
If it points, it means the array has no elements.
Assign front =0;
Else || increment Front by '1'
front = front+1;
Otherwise,
Front=front+1;
There is another approach to implement deque which is done using a doubly linked-list. The approach is quite similar with some minor changes and those minor changes can be implemented using the following pseudo-code below.
Example 2: Using Double linked-list
#include<iostream>
using namespace std;
class node
{
public:
int data;
node* next;
node* prev;
};
class Dequey{
public:
node* newnode;
node* temp;
node* head;
node* tail;
int i,n;
void create_node(){
node* newnode = new node();
cin>>newnode->data;
newnode->next = NULL;
newnode->prev = NULL;
}
void init(){
head = NULL;
tail = NULL;
cout<<"Please enter the first node data"<<endl;
create_node();
head = newnode;
tail = newnode;
}
void insertion_beg(){
create_node();
newnode->next = head;
head->prev= newnode;
head = head->prev;
}
void insertion_end(){
create_node();
newnode->prev = tail;
tail->next = newnode;
tail = tail->next;
}
void deletion_beg(){
head = head->next;
}
void deletion_end(){
tail = tail->prev;
tail->next = NULL;
}
void display()
{
temp = head;
while(temp != tail){
cout<<temp->data<<" ";
temp = temp->next;
}
}
};
int main(){
Dequey d;
int choice=0,flag=0;
d.init();
while(1)
{
cout<<endl<<"1. Insertion at Beginning \n2. Insertion at End \n3. Deletion at Beginning \n4. Deletion at End \n5. EXIT"<<endl;
cin>>choice;
if(choice==5)
break;
switch(choice)
{
case 1:
d.insertion_beg();
break;
case 2:
d.insertion_end();
break;
case 3:
d.deletion_beg();
break;
case 4:
d.deletion_end();
break;
case 5:
flag = 1;
break;
}
}
d.display();
return 0;
}
Output:
Explanation:
The above code is the illustration of deque served with the Doubly linked list. We already know that in a Doubly linked-list, each node apart from storing its data has two links. The first link points to the previous node in the list and the second link points to the next node in the list.
Using this approach, we have assigned the switch cases so that the insertion and deletion can take place at the ends whenever the pointer points to the first link, then the second, and so on to the next node in the list. This ensures that irrespective of the differences in the memory addresses assigned, the links keep pointing consistently and store data with the help of those two links.