How to get the value of pi in C++
How to get the value of pi in C++
In this article, we will discuss how to get the value of pi in C++ with several methods.
Introduction to Pi:
The circumference ratio to a circle's diameter is known as pi (Π), a mathematical constant. It cannot be expressed as a fraction of two integers because it is an irrational number. In addition, pi is a transcendental number, meaning no polynomial with rational coefficients can have pi as its root.
Pi is an essential number in mathematics because it appears in many formulae and equations, including ones involving spheres, circles, and trigonometric functions. In numerous branches of science and engineering, including computer science, physics, and astronomy, it is also employed.
The value of pi (Π) is approximately 3.14159.
Although it has been estimated to be trillions of decimal places, the precise value of pi is unknown. It is usually calculated to two decimal places, or 3.14, in everyday use.
Include the <cmath> Header:
The <cmath> header must be included to use mathematical functions. A collection of parts to carry out typical mathematical operations is defined in this header.
A named location in memory that stores a value is called a variable. Any data, including characters, strings, integers, and floating-point numbers, can be stored in variables.
The data type of a variable and its name must be specified before it can be declared. For instance, the code below would be used to declare a double-type variable called pi:
double pi;
Double-precision floating-point numbers are stored using the double data type. It indicates that double variables have a high degree of accuracy when storing numbers.
We store it using the double data type because Pi's value is a highly accurate floating-point number. It is significant because Pi cannot be stated as a fraction of two integers since it is an irrational number. Consequently, we must employ a data type that has a high level of accuracy when storing numbers.
An illustration of declaring and initializing a double variable to hold the value of Pi is provided here:
double pi = 3.14159;
This code initializes a double-type variable called pi to the value of pi.
Variables:
A variable can be used in our code just like any other variable once declared and initialized. For instance, the variable's value can be printed, used in computations, or passed as an argument to a function.
Example:
Here's an illustration of how to use our code's pi variable:
#include <iostream>
double pi = 3.14159;
double radius = 10.0; // Initialize the radius variable
int main() {
// Print the value of the pi variable
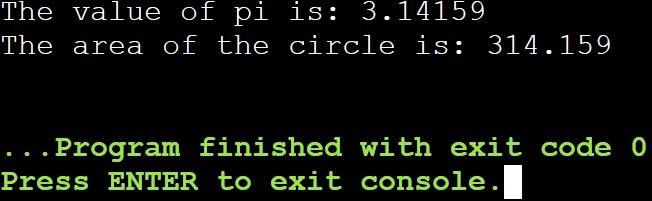
std::cout << "The value of pi is: " << pi << std::endl;
// Calculate the area of a circle with the given radius
double area_of_circle = pi * radius * radius;
// Print the area of the circle
std::cout << "The area of the circle is: " << area_of_circle << std::endl;
return 0;
}
Output:
Pi Calculation Algorithm:
There are several algorithms to calculate the value of pi. Some of them are as follows:
1. Arctan Series (Leibniz Series)
Formula: Π = 4 * (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ...)
Idea: It is a simple method for approximating Pi based on the arctangent function. Fractions are added and subtracted using an alternating series. The approximation approaches the true value of Pi more closely the more terms we add to the series. However, it does converge rather slowly.
2. Monte Carlo Method
Principle: The Monte Carlo Method uses a probabilistic methodology. It uses geometric shape properties and random sampling to estimate Pi.
Idea: Inside a square, we position a circle with a known radius. We can determine the ratio of points that fall inside the circle to the total number of points by randomly creating points within the square. The accuracy of the Pi estimate increases with the number of random points. It's a straightforward, albeit random, method of estimating Pi.
3. Chudnovsky Algorithm
Formula: Π = 426880 * sqrt(10005) / K (with K being calculated as a complex sum)
Idea: The Chudnovsky Algorithm is a highly precise, fast-converging, and efficient technique. It requires intricate mathematical computations, such as exponentials and factorials. This algorithm works well for individuals who need exact values of Pi. It is beneficial for complex calculations and applications that call for a high degree of accuracy.
Arctan Series (Leibniz Series):
Let's take an example to illustrate the value of Pi using the Arctan Series (Leibniz Series) in C++:
#include <iostream>
int main() {
int n; // Number of terms to calculate (higher value for more precision)
double pi = 0.0;
int sign = 1; // Initialize the sign to positive
// Prompt the user to enter the number of terms
std::cout << "Enter the number of terms to calculate Pi: ";
std::cin >> n;
if (n > 0) {
double newPi = 0.0;
for (int i = 0; i < n; ++i) {
newPi += sign / (2.0 * i + 1.0);
sign = -sign; // Toggle the sign for each term
}
newPi *= 4; // Multiply by 4 to get the value of Pi
// Print the calculated value of Pi
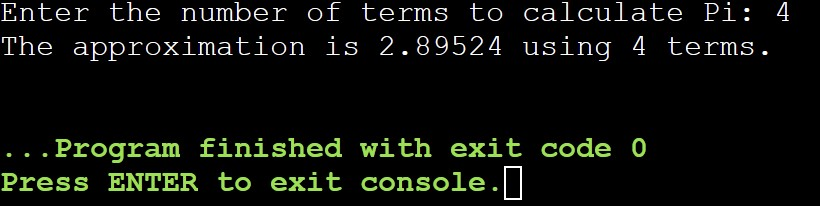
std::cout << "The approximation is " << newPi << " using " << n << " terms.\n";
} else {
std::cout << "Number of terms must be greater than 0.\n";
}
return 0;
}
Output:
Monte Carlo Method:
Let's take an example to illustrate the value of Pi using the Monte Carlo Method in C++:
#include <iostream>
#include <random>
int main() {
// Input parameters
int nTrials = static_cast<int>(10E4);
double radius = 1.0;
// Counter for the points inside the circle
int nInside = 0;
// Create a random number generator
std::random_device rd;
std::default_random_engine generator(rd());
std::uniform_real_distribution<double> distribution(-1.0, 1.0);
for (int i = 0; i < nTrials; ++i) {
double x = distribution(generator);
double y = distribution(generator);
// Check if the points are inside the circle or not
if (x * x + y * y <= radius * radius) {
nInside++;
}
}
double area = 4.0 * nInside / nTrials;
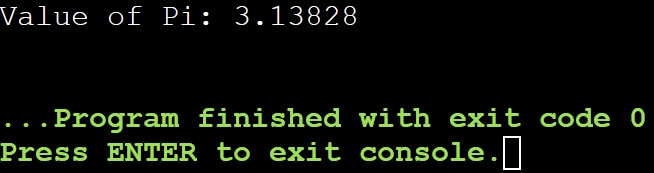
std::cout << "Value of Pi: " << area << std::endl;
return 0;
}
Output:
Chudnovsky Algorithm:
Let's take an example to illustrate the value of Pi using the Chudnovsky Algorithm in C++:
#include <iostream>
#include <cmath>
#include <iomanip>
// Function to calculate the factorial of an integer
long long calculateFactorial(int n) {
long long result = 1;
for (int i = n; i > 1; i--) {
result *= i;
}
return result;
}
int main() {
long double pi = 0.0;
int precision = 10;
for (int k = 0; k <= precision; k++) {
long double numerator = pow(-1, k) * calculateFactorial(6 * k) * (13591409 + 545140134 * k);
long double denominator = calculateFactorial(3 * k) * pow(calculateFactorial(k), 3) * pow(640320, 3 * k + 1.5);
pi += numerator / denominator;
}
pi = 1.0 / (12 * pi);
// Set the output to display more decimal places for precision
std::cout << std::fixed << std::setprecision(80) << pi << '\n';
return 0;
}
Output:

Pi is an arithmetic constant that has numerous practical uses in everyday life. Here are some instances:
Geometry:
- Pi is used to calculate the area and circumference of circles.
- Pi is used to calculate the volume of spheres and cylinders.
- Pi is used to calculate the surface area of spheres and cylinders.
- Pi calculates the length of arcs and the size of sectors.
Physics:
- Pi is used to calculate the wavelength of light and other electromagnetic waves.
- Pi is used to calculate the period and frequency of oscillations.
- Pi is used to calculate the angular momentum of rotating objects.
- Pi is used to calculate the gravitational force between two objects.
Engineering:
- Pi is used to design bridges, buildings, and other structures.
- Pi is used to create gears and other mechanical components.
- Pi is used to make electrical and electronic components.
- Pi is used to develop computer software and algorithms.
Here are a few particular instances of real-world applications for Pi:
- GPS navigation: GPS satellites utilizes pi to determine their locations and send navigation signals to GPS receivers.
- Computer graphics: Pi is a tool used in computer graphics to render curved shapes, such as circles.
- Medical imaging: Pi creates three-dimensional images of the human body in procedures like CT and MRI scans.
- Astronomy: The orbits of planets and stars are computed using pi.
- Finance: Pi is used to compute risk and return in financial models.
Pi is a fundamental mathematical constant that is applied in a wide range of engineering and scientific disciplines. The variety of applications it uses shows how important it is in real life.
Practical uses of Pi:
- Aerodynamics: The lift and drag of aircraft and other aerodynamic vehicles are computed using pi.
- Acoustics: Pi is used in fluid mechanics to add fluid flow through pipes and other systems.
- Acoustics: The sound wave's propagation can be calculated using pi.
- Optics: In optics, the reflection and refraction of light are calculated using pi.
Probability and statistics:
- Pi is used in statistics and probability to evaluate data and determine the likelihood of occurrences.