C++ Program: Matrix Multiplication

Matrix Multiplication in C++

What is a Matrix?

A matrix is a set of numbers in the form of rows and columns forming a rectangular array. It includes numbers, which are often called entries or elements. Matrix has wide application in the field of engineering and mathematics and is solely intended to solve various business logical problems comprising its applications.

A matrix typically looks like an array where there are N rows and M columns. It also consists of symbols and expressions.

Matrix multiplication has been defined by a set of rules for multiplying. There are although various ways of representing matrix. Below is a pictorial representation of a usual matrix.

Before proceeding to check how matrix multiplication is carried out in C++, we need prior knowledge of multi-dimensional arrays or say 2-D arrays. A matrix in general, is a multi-dimensional array in C++.

There a multi-dimensional array is of the form

 int arr[rows][columns]

Where rows and columns are integer values that can be initialized or can be taken input.

Let us now look at different approaches of carrying out matrix multiplication in C++.

Example:

#include <bits/stdc++.h>
 using namespace std;
 #define N 4
 void MatrixMultiply(int matrix1[][N],
               int matrix2[][N],
               int result[][N])
 {
     int i, j, k;
     for (i = 0; i < N; i++) {
         for (j = 0; j < N; j++) {
             result[i][j] = 0;
             for (k = 0; k < N; k++)
                 result[i][j] += matrix1[i][k] * matrix2[k][j];
         }
     }
 }
 int main()
 {
     int i, j;
     int result[N][N]; // To store result
     int matrix1[N][N] = { { 1, 1, 1, 1 },
                        { 2, 2, 2, 2 },
                        { 3, 3, 3, 3 },
                        { 4, 4, 4, 4 } };
     int matrix2[N][N] = { { 1, 1, 1, 1 },
                        { 2, 2, 2, 2 },
                        { 3, 3, 3, 3 },
                        { 4, 4, 4, 4 } };
 MatrixMultiply(matrix1, matrix2, result);
 cout << "Matrix after multiplication is:  \n";
     for (i = 0; i < N; i++) {
         for (j = 0; j < N; j++)
             cout << result[i][j] << " ";
         cout << "\n";
 }
 return 0;
 } 

Output:

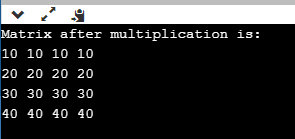
Explanation:

In the above code, we have defined a function 'MatrixMultiply' which takes as arguments 'matrix1', 'matrix2', and 'result' to carry out multiplication. The following algorithm is used for the process:

Start

1. Declare function MatrixMultiply with arguments matrix1,  matrix2, and result.
2. In the function, iterate thorough the elements using two loops for rows and columns.
3. Declare the variable result as result=matrix1*matrix2
4. In the driver code, initialize the matrix1 and matrix2 with their respective values in rows and columns.
5. Call the function MatrixMultiply in the driver code which multiplies both the matrices.
6. Print the result in matrix form as console output.

Stop

Logic:

The logic is to iterate through nested loops. If both the matrices are initially defined, we can multiply them using the formula of rows and columns where a1 *b1 and b2*a2 and so on. This brings out the result in the form of another matrix consisting of values which are the results of the multiplication of both the matrices.

Decimal to Binary Conversion in C++

We have come across the term Binary which is the elementary language through which computers communicate with each other. We can use whole numbers and natural numbers to represent our values. But a compiler converts the number to binary to facilitate the computer to understand our input. This is where decimal to binary conversion comes into play.

Binary numbers form the basis of communication in a computer system. Let us know how a decimal number is converted into a binary value through the image below:

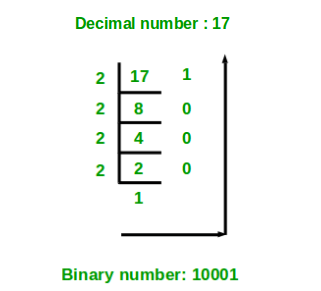
Here, we first find out the LCM of a number, and the remainder is written if it is not a perfect multiple of the number. The obtained value on the right side i.e. the remainder is read from bottom to top which gives us the binary number of 17.

Let us now look at the approaches and logical explanations of doing the same using C++.

Example 1: Using functions

#include <bits/stdc++.h>
 using namespace std;
 void DecimalToBinary(int number)
 {
     int binaryNumber[32];
     int i = 0;
     while (number > 0) {
         binaryNumber[i] = number % 2;
         number = number / 2;
         i++;
     }
     for (int j = i - 1; j >= 0; j--)
         cout << binaryNumber[j];
 }
 int main()
 {
     int number;
     cout<<"Enter number to get binary value: ";
     cin>>number;
     DecimalToBinary(number);
     return 0;
 } 

Output:

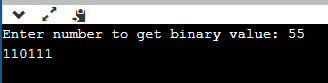
Explanation:

In the above code, we have defined a function 'Decimal to binary' and the variable 'number'. The process can be explained through the following algorithmic explanation:

1. Store the number when it is divided by 2 in the array.

• Number needs to be divided by 2

• Run a loop until the number is less than zero

• print the remainder in the reverse order.

Example 2: Using recursion

#include <bits/stdc++.h>
 using namespace std;
 void DeciToBin(int number)
 {
     if (number == 0) {
         cout << "0";
         return;
     }
     DeciToBin(number / 2);
     cout << number % 2;
 }
 int main()
 {
     int number;
     cout<<"Enter number to get the binary value: ";
     cin>>number;
     DeciToBin(number);
     return 0;
 } 

Output:

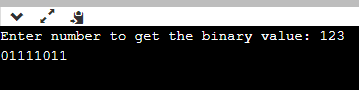
Explanation:

The above is quite similar to the previous program where we defined a function having the argument as a number which is to be taken as an input by the user. Here, we have similarly used a recursive approach where the function is repeating itself until the given condition is reached.

The recursive approach reduces the code complexity and enhances code-readability. Later, in the driver code, the function automatically call itself as soon as it gets the argument.

Although, the recursive provides better code readability and understanding the time complexity is increased when we use recursion in a code. Since the function keeps calling itself, it keeps repeating until the end condition is reached thereby increasing time consumption as compared to other native approaches.