Depth First Search Program to Traverse a Graph in C++

Depth First Search (DFS) is a technique that is used for transversing the graph. The process of Depth First Search (DFS) starts from the root node and then next comes to the adjacent nodes. This means Depth First Search (DFS) expands the node depth-wise. The traversing process stops when it encounters a node with no child node. Once the leaf nodes come then, the whole process repeats again. Unlike the BFS, the Depth First Search (DFS) also expands its process breadth-wise. We use the stack data structure to expand the whole process in Depth First Search (DFS). The unexplored nodes are also called discovery edges, while the already visited node is called block nodes.

Now, we will see the algorithm and pseudo code for the Depth First Search (DFS).

• Step 1: We have to insert the root node in a graph of the stack.
• Step 2: We have to pop the item from the stack and start visiting the nodes.
• Step 3: Then, we have to find all the adjacent nodes and mark them as visited.
• Step 4: Repeat steps two and step 3 until the whole stack becomes empty.

The pseudo-code for the Depth First Search (DFS) is below.

Procedure DFS(G,x)
 G>graph to be traversed.
  x> starting nodes.
Begin
x.visited= true
for each v belongs to G.Adj[x]
if v.visited==false
dfs ( G, v)
end procedure.
For each x belongs to G
x. visited = false
 for each x belongs to G
DFS(G,x)
}   

Traversal Process of Depth First Search (DFS) with Illusion

Let us start the discussion of the traversal of Depth First Search (DFS) in a stepwise manner. We will be going to use the same graph for the whole traversal process.

Let us take 0 as the starting node. Then, we mention 0 as the visited, then start the traversing process with 0. Then, we have to push all the neighboring nodes in manner wise in the stack.

Then, we have to perform the above process in node one, i.e., top of the stack. Then, we have to mark node one as visited then add node 1 to the marked list.

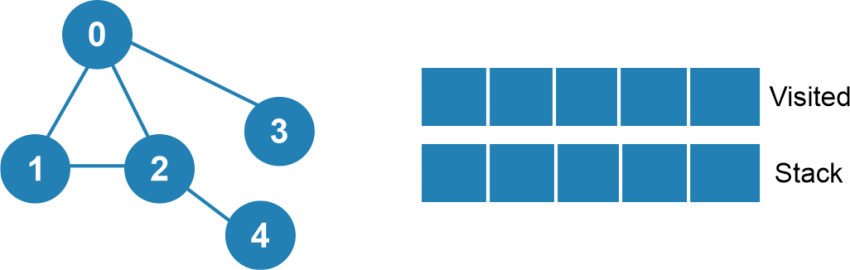
 Now, we have to look for the adjacent node of 1. As 0 is already visited, then we have to perform the operation in node 2.

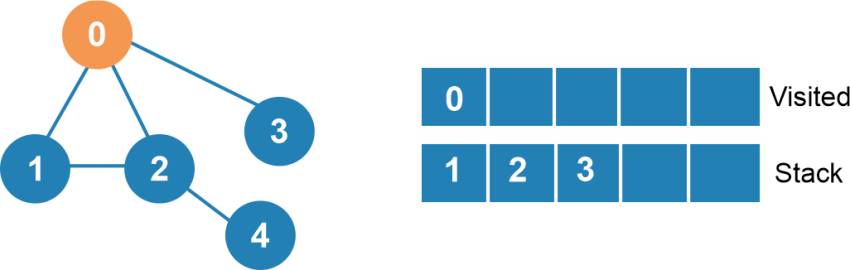
Next, we have to mark node two as visited and add node two to the visited list.

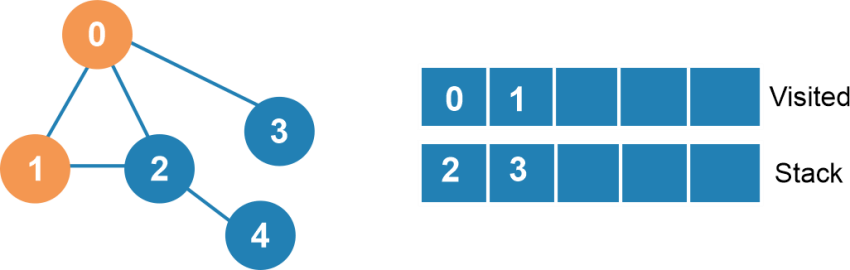
Next, we have to mark node four as marked and add node 4 to the visited list.

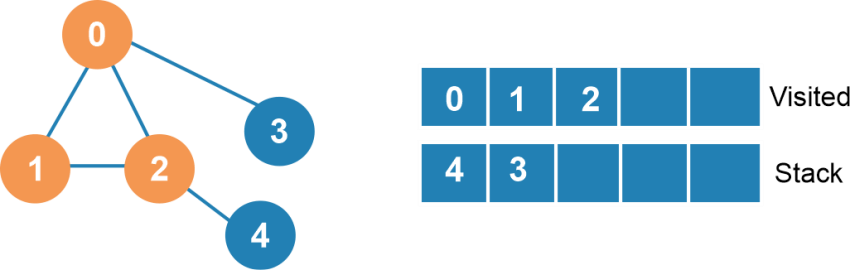
Next, we have to mark node three as marked and add node 3 to the visited list.

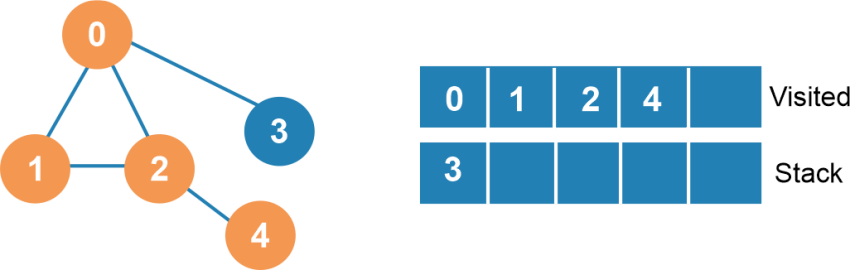
Now, the whole stack becomes empty. So, we have to stop our traversal process.

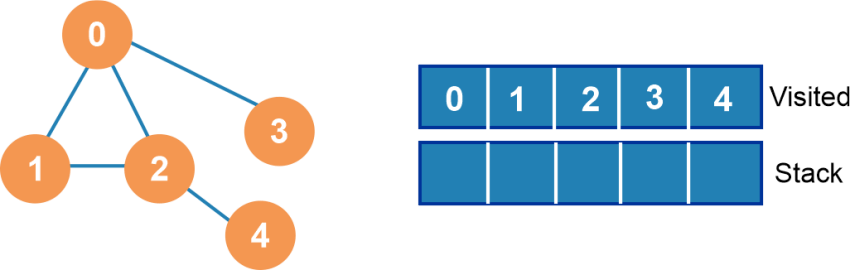
Implementation of Depth First Search (DFS)

#include <iostream> 
#include <list> 
using namespace std; 
class DFSGraph 
{ 
int V;   
list<int> *adjList;   
void DFS_util(int v, bool visited[]);  
public: 
   
DFSGraph(int V)
    {
 this->V = V; 
 adjList = new list<int>[V]; 
    }
   
void addEdge(int v, int w){
adjList[v].push_back(w);
    }
     
void DFS();   
}; 
void DFSGraph::DFS_util(int v, bool visited[]) 
{ 
    
visited[v] = true; 
cout << v << " "; 
   
    
list<int>::iterator i; 
for(i = adjList[v].begin(); i != adjList[v].end(); ++i) 
if(!visited[*i]) 
DFS_util(*i, visited); 
} 
 
void DFSGraph::DFS() 
{ 
  
bool *visited = new bool[V]; 
for (int i = 0; i < V; i++) 
visited[i] = false; 
   
   
for (int i = 0; i < V; i++) 
if (visited[i] == false) 
DFS_util(i, visited); 
} 
   
int main() 
{ 
  
DFSGraph gdfs(5); 
gdfs.addEdge(0, 1); 
gdfs.addEdge(0, 2); 
gdfs.addEdge(0, 3);
gdfs.addEdge(1, 2); 
gdfs.addEdge(2, 4);
gdfs.addEdge(3, 3); 
gdfs.addEdge(4, 4);


cout << "Depth-first traversal for the given graph:"<<endl; 
gdfs.DFS(); 
   
return 0; 
}

Output:

Depth-first traversal for the given graph:
0 1 2 4 3

Runtime Analysis

The time complexity for Depth First Search (DFS) is O (|V|+|E|) which is similar to the breath first search. 

Here V= number of vertices.

E= number of edges given in the graph.

Handling a Disconnected Graph

The above code traverses only the vertices reachable from a given source vertex. All the vertices may not be reachable from a given vertex, as in a disconnected graph. To do a complete DFS traversal of such graphs, run DFS from all unvisited nodes after a DFS. The recursive function remains the same.

Follow the steps given below to solve the problem:

• Create a recursive function that takes the index of the node and a visited array.
• Mark the current node as visited and print the node.
• Traverse all the adjacent and unmarked nodes and call the recursive function with the index of the adjacent node.
• Run a loop from 0 to the number of vertices and check if the node is unvisited in the previous DFS, then call the recursive function with the current node.

Iterative Depth First Search (DFS)

The above Depth First Search (DFS) implementation is recursive in nature. It is used to call the function from the stack. But we have another method to implement the iterative depth-first search. We use the explicit stack method to hold the visited nodes in this method. Below we show the implementation of the iterative depth-first search method in a program.

#include<bits/stdc++.h> 
using namespace std; 
class Graph 
{ 
int V;   
list<int> *adjList;   
public: 
Graph(int V) 
    {
this->V = V; 
adjList = new list<int>[V]; 
    }
void addEdge(int v, int w)  
    {
adjList[v].push_back(w):
    }
void DFS(); 
   
    
void DFSUtil(int s, vector<bool> &visited); 
}; 
   


void Graph::DFSUtil(int s, vector<bool> &visited) 
{ 
   
stack<int> dfsstack; 
dfsstack.push(s); 
   
while (!dfsstack.empty()) 
    { 
         
        s = dfsstack.top(); 
       dfsstack.pop(); 
   
        
 if (!visited[s]) 
        { 
cout << s << " "; 
visited[s] = true; 
        } 
  
for (auto i = adjList[s].begin(); i != adjList[s].end(); ++i) 
if (!visited[*i]) 
dfsstack.push(*i); 
    } 
} 
void Graph::DFS() 
{ 
   
vector<bool> visited(V, false); 
   
for (int i = 0; i < V; i++) 
if (!visited[i]) 
DFSUtil(i, visited); 
} 
   
//main program
int main() 
{ 
    Graph gidfs(5); 
gidfs.addEdge(0, 1); 
gidfs.addEdge(0, 2); 
gidfs.addEdge(0, 3);
gidfs.addEdge(1, 2); 
gidfs.addEdge(2, 4);
gidfs.addEdge(3, 3); 
gidfs.addEdge(4, 4);
  
cout << "Output of Iterative Depth-first traversal:\n"; 
gidfs.DFS(); 
   
return 0; 
}

Output:

Output of Iterative Depth-first traversal:
0 3 2 4 1

Here, we use the same graph for the implementation of the iterative depth-first search. There is a difference in the output. It is because of the iterative implementation of a stack. As the stack flow LIFO (Last in First Out), there is a difference in the sequence of Depth First search (DFS).

Applications of DFS

• Detecting Cycles In The Graph: If we find a back edge while performing DFS in a graph, we can conclude that the graph has a cycle. Hence DFS is used to detect the cycles in a graph.
• Pathfinding: Given two vertices, x and y, we can find the path between x and y using DFS. We start with vertex x and then push all the vertices on the way to the stack till we encounter y. The contents of the stack give the path between x and y.
• Minimum Spanning Tree and Shortest Path: DFS traversal of the un-weighted graph gives us a minimum spanning tree and shortest path between nodes.
• Topological Sorting: We use topological sorting to schedule the jobs from the given dependencies among jobs. In computer science, we use it primarily to resolve symbol dependencies in linkers, data serialization, instruction scheduling, etc. DFS is widely used in Topological sorting.

Conclusion

In the last couple of tutorials, we have explored more about the two traversal techniques for graphs, i.e., BFS and DFS. We have seen the differences as well as the applications of both methods. BFS and DFS achieve the same outcome of visiting all nodes of a graph, but they differ in the order of the output and how it is done.

We have also seen the implementation of both techniques. While BFS uses a queue, DFS uses stacks to implement the method. With this, we conclude the tutorial on traversal techniques for graphs. We can also use BFS and DFS on trees.