Tree Data Structure in C++

A tree in computer science is a hierarchical concept that has nodes connected by edges. It is a bottom-up organization because it has a single root node, and all nodes descend from that point to show hierarchical relations or organizations. Therefore, in a tree, each node will store information, and it may or may not have several descendants that form one of the branches.

The tree is a type of data structure that stores information in an orderly fashion. It has nodes that are used for storing data and links, which are connections between these two ends. Different from items organized linearly in lists or arrays, the branching nature of a tree is nonlinear and begins with an initial root node. Each tree can have any number of descendants or even none, so the resulting structure becomes hierarchical because each node has a child. Trees are common applications in computer science for algorithmic implementation efficiency of data structures that illustrate parent-child relationships.

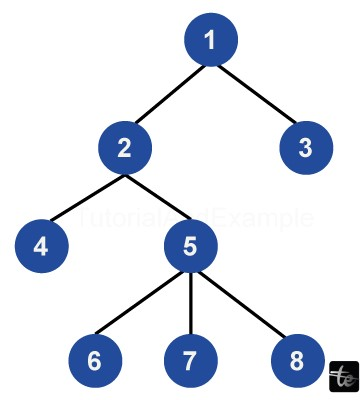
Why Tree Data Structure:

In relation to linear data structures, including arrays and linked lists, among other tree-based provide numerous benefits. Costs of time grow as volumes in linear structures data are greater because of the sequential storing of information. However, this is a disadvantage in the current computational regime.

This, however, is different from other tree structures, which present a nonlinear configuration that leads to an effective solution. This enables faster and more convenient access to information. Trees support the optimized process; therefore, they can be used for situations that require quick and proficient data retrieval or manipulation. Trees provide more elasticity and scalability to meet modern computing needs.

Fundamental Concepts in Tree Data Structures:

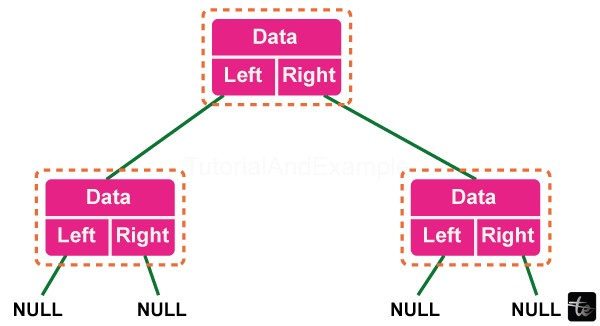
Node: A node is an element of the tree that has references (pointers) to its child nodes but also a key or value. The nodes that are at the end of all of these paths in a tree-like structure are called leaf or external nodes since they have no connection with their child elements. On the other hand, an internal node is a leaf with at least one child.

Edge: Edges in a tree symbolize the links between nodes that form internal bonding among elements of the structure.

Tree Traversals:

In C++, the term "tree traversals" describes the procedures used to visit and handle each node in a binary tree in a particular order. Tree traversals can be divided into three main categories: inorder, preorder, and postorder.

Inorder Traversal:

An inorder traversal processes the binary tree by examining its left subtree first, processing the current or root node next, and then traversing its right subtree. Applying this traversal approach to a binary search tree ensures that the nodes are handled according to their values in ascending order. It is a systematic approach of traversing a binary search tree's node in order of smallest to largest.

Syntax:

void inorderTraversal(TreeNode* root) {

    if (root != nullptr) {

inorderTraversal(root->left);

        cout << root->data << " ";

inorderTraversal(root->right);

    }

}

Preorder Traversal:

A preorder traversal explores the binary tree starting from the root node. It first processes the root node, then moves on to the left subtree, and finally, the right subtree. This sequential method is a systematic way to investigate nodes in the tree from top to bottom since it guarantees that the root is encountered before any of its child nodes.

Syntax:

void preorderTraversal(TreeNode* root) {

    if (root != nullptr) {

        cout << root->data << " ";

preorderTraversal(root->left);

preorderTraversal(root->right);

    }

}

Postorder Traversal:

In a postorder traversal, the root node is processed last, along with left subtree nodes, at some point in time after exploring right and (leftmost) neighbor trees. This traversal technique provides a systematic approach to investigate and process nodes in a bottom-up way through tree structure by ensuring that the child node is accessed before the parent.

Syntax:

void postorderTraversal(TreeNode* root) {

if (root != nullptr) {

postorderTraversal(root->left);

postorderTraversal(root->right);

cout << root->data << " ";

}

}

Varieties of Tree Data Structures:

Different types of tree data structures exist; each type has a specific application and merits in assisting in organizing and searching the information optimally. The following are some typical kinds of tree data structures:

1. Binary tree:

All nodes in a binary tree have two children—the left and right. Almost always used for binary search, this building block can serve as an efficient foundation for building more complex trees. This tree binary structure in which nodes have two children at the same time is appropriate for comparison.

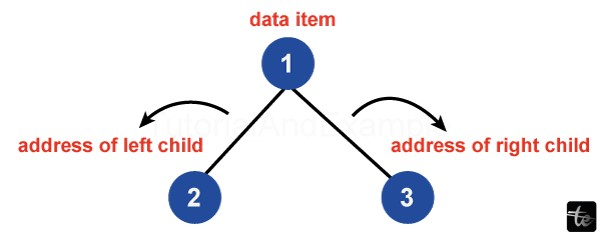
Understanding Different Types of Binary Trees:

Full Binary Tree: In a full binary tree, each internal (non-leaf) node has two offspring or none at all. This is a unique type of binary tree. With this arrangement, the tree's equilibrium is maintained, and node consumption is optimized.

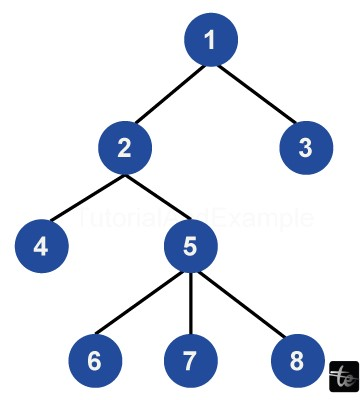
Node Structure in Binary Trees: Data and Pointers

Nodes, as structures with two pointers to other structures of the same type and a data member, are represented by binary trees. This structure of encasing the data into a node and forming links to its left and right child nodes through pointers actually serves as the core basis for building a binary tree.

struct TreeNode {

int data;

TreeNode* left;

TreeNode* right;

};

Implementation of binary tree:

#include <iostream>

// Structure of a node in a binary tree

struct TreeNode {

in#include <iostream>

// Structure of a node in a binary tree

struct TreeNode {

    int data;

    TreeNode* left;

    TreeNode* right;

    // Constructor

    TreeNode(int value) : data(value), left(nullptr), right(nullptr) {}

};

// Function to insert a new node into the binary tree

TreeNode* insert(TreeNode* root, int value) {

    if (root == nullptr) {

        return new TreeNode(value);

    }

    if (value < root->data) {

        root->left = insert(root->left, value);

    } else {

        root->right = insert(root->right, value);

    }

    return root;

}

// Function to perform in-order traversal of the binary tree

void inorderTraversal(TreeNode* root) {

    if (root != nullptr) {

        inorderTraversal(root->left);

        std::cout << root->data << " ";

        inorderTraversal(root->right);

    }

}

int main() {

    // Creating an empty binary tree

    TreeNode* root = nullptr;

    // Binary tree elements addition

    root = insert(root, 50);

    insert(root, 30);

    insert(root, 20);

    insert(root, 40);

    insert(root, 70);

    insert(root, 60);

    insert(root, 80);

    // Display elements using in-order traversal.

    std::cout << "Inorder Traversal: ";

    inorderTraversal(root);

    std::cout << std::endl;

    return 0;

}

Output:

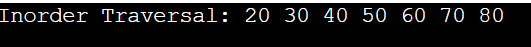
Applications of Binary Tree:

A binary tree is a foundational data structure in computer science, and C++ offers several applications of binary trees. Its key application is Binary Search Trees (BSTs), where the insertion, deletion, and search operations are highly efficient due to a proper structure. Expression trees represent an approach to mathematical representation using binary tree structures that enable systematic evaluation. Huffman coding trees provide the best prefix codes for character frequencies, using binary tree structures in data compression. The other application where priority queues and heap sorting are possible is binary heaps, which offer constant time access to the minimum or maximum elements. Since binary trees simplify the indexation and organizing of directory structures, file searches are done faster. Machine learning uses the decision tree to guide classification and choice systems. In strategic games, the game trees represent possible moves and outcomes.

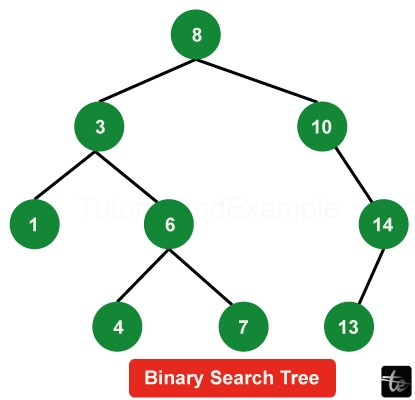
Binary Search Tree:

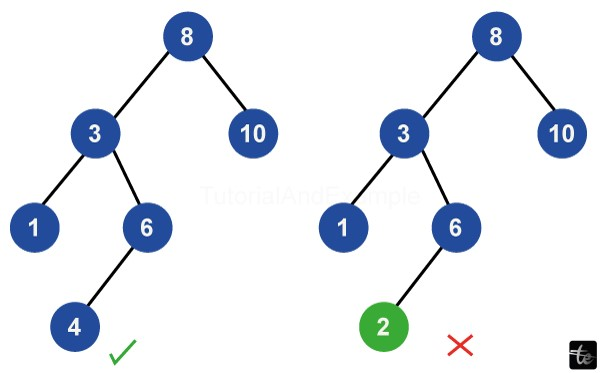
Then, a Binary Search Tree (BST) is designed to manage an orderly list of numbers. Binary indicates that there can be at most two children for every node in the tree. A BST allows us to do searches quickly because it can compute whether a number is present in O(log (n)) time.

The following special characteristics set a binary search tree apart from the regular binary tree:

All nodes have values in their left subtree that are lower than the value of the node itself.

However, all nodes in the right subtree of a given node have values higher than their own.

These properties are also recursively true for the left and right subtrees of every node, leading to a BST in the form of a hierarchical structure inside the total tree.

Notably, these characteristics also apply recursively to the left and right subtrees of every node, creating a hierarchical structure of Binary Search Trees inside the total tree.

A binary search tree can be subjected to two basic procedures, which are as follows:

Search Operation:

The search for a particular integer, X, in a binary search tree starts at the root. Following the rule that items in the left subtree are smaller and those in the right subtree are larger, moving to the left or right subtree is determined by comparing X and the root value. Until the value X is located, indicating a successful search, or until no more traversal is available, indicating an unsuccessful search, this procedure iterates. The search yields True if X is discovered at any time during the iteration; otherwise, it yields False.

Code:

#include <iostream>

// The following is a node structure for the binary search tree.

struct TreeNode {

int data;

TreeNode* left;

TreeNode* right;

TreeNode(int value) : data(value), left(nullptr), right(nullptr) {}

};

// Search function in BST

bool search(TreeNode* root, int target) {

// Base case: When the root is null, then the target will not be found

if (root == nullptr) {

return false;

}

// If the target matches with data at the current node, it is found

if (root->data == target) {

return true;

}

//If the element to be searched is smaller than that of the current node, then look in the left subtree

if (target < root->data) {

return search(root->left, target);

}

// If the target is higher than the value of the current node, search in its right subtree

return search(root->right, target);

}

int main() {

// Implementing an example Binary Search Tree

TreeNode* root = new TreeNode(5);

root->left = new TreeNode(3);

root->right = new TreeNode(8);

root->left->left = new TreeNode(2);

root->left->right = new TreeNode(4);

root->right->left = new TreeNode(7);

root->right->right = new TreeNode(9);

// Finding values in the BST

int target1 = 4;

int target2 = 6;

if (search(root, target1)) {

std::cout << "target1 is found in the BST.\n"<< std::endl;

} else {

std::cout << " target1 is absent in the BST.\n" << std::endl;

}

if (search(root, target2)) {

std::cout << "target2 is in the BST.\n"<<std::endl;

} else {

std::cout << " target2 is not available in the BST.\n"<<std::endl;

}

return 0;

}

Output:

#include <iostream>

using namespace std;

class BST {

Public:

int data;

BST* left;

BST* right;

// Parameterized constructor.

BST(int value) {

data = value;

left = right = nullptr;

}

// Insert function.

BST* Insert(int value) {

if (value < data) {

// Enter left node data if the value is smaller than ‘data.’

if (left == nullptr) {

left = new BST(value);

} else {

left->Insert(value);

}

} else if (value > data) {

// Then, insert the right node data if 'value' is larger than ‘data.’

if (right == nullptr) {

right = new BST(value);

} else {

right->Insert(value);

}

}

return this;

}

// Inorder traversal function.

// This provides the sorted data.

void Inorder() {

if (left != nullptr) {

left->Inorder();

}

cout << data << " ";

if (right != nullptr) {

right->Inorder();

}

}

};

// Driver code

int main() {

BST* root = new BST(50);

root->Insert(30)->Insert(20)->Insert(40)->Insert(70)->Insert(60)->Insert(80);

// Displays the sorted BST using an inorder traversal.

root->Inorder();

return 0;

}

Output:

#include <iostream>

using namespace std;

struct Node {

    int key;

    struct Node *left, *right;

};

Node* newNode(int item) {

    Node* temp = new Node;

    temp->key = item;

    temp->left = temp->right = NULL;

    return temp;

}

Node* insert(Node* node, int key) {

    if (node == NULL)

        return newNode(key);

    if (key < node->key)

        node->left = insert(node->left, key);

    else if (key > node->key)

        node->right = insert(node->right, key);

    return node;

}

Node* deleteNode(Node* root, int k) {

    if (root == NULL)

        return root;

    if (root->key > k) {

        root->left = deleteNode(root->left, k);

    } else if (root->key < k) {

        root->right = deleteNode(root->right, k);

    } else {

        if (root->left == NULL) {

            Node* temp = root->right;

            delete root;

            return temp;

        } else if (root->right == NULL) {

            Node* temp = root->left;

            delete root;

            return temp;

        }

        Node* succParent = root;

        Node* succ = root->right;

        while (succ->left != NULL) {

            succParent = succ;

            succ = succ->left;

        }

        if (succParent != root)

            succParent->left = succ->right;

        else

            succParent->right = succ->right;

        root->key = succ->key;

        delete succ;

    }

    return root;

}

void inorder(Node* root) {

    if (root != NULL) {

        inorder(root->left);

        cout << root->key << " ";

        inorder(root->right);

    }

}

int main() {

    Node* root = NULL;

    root = insert(root, 50);

    insert(root, 30);

    insert(root, 20);

    insert(root, 40);

    insert(root, 70);

    insert(root, 60);

    cout << "Original BST: ";

    inorder(root);

    cout << "\n\nDelete a Leaf Node: 20\n";

    root = deleteNode(root, 20);

    cout << "Modified BST tree after deleting Leaf Node: \n";

    inorder(root);

    cout << "\n\nDelete Node with single child: 70\n";

    root = deleteNode(root, 70);

    cout << "Modified BST tree after deleting single child Node: \n";

    inorder(root);

    cout << "\n\nDelete Node with both child: 50\n";

    root = deleteNode(root, 50);

    cout << "Modified BST tree after deleting both child Node: \n";

    inorder(root);

    return 0;

}

Output:

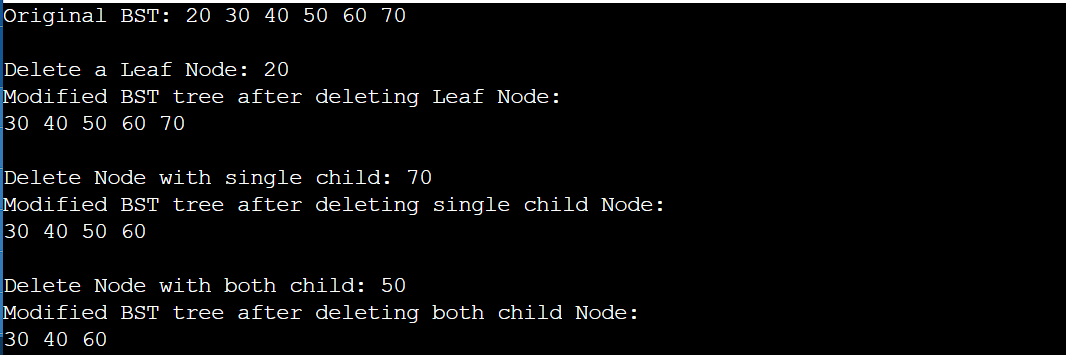
Applications of BST:

Databases, compilers, and file systems all frequently use Binary Search Trees (BSTs) for effective indexing, symbol table management, and fast file retrieval. They are essential to memory management systems, auto-complete and spell-checking programs, and networking for routing tables. BSTs are also used in frequency counting tasks, such as word frequency analysis in documents and in genetic evolution studies, where they represent phylogenetic trees. BSTs are adaptable and useful in a variety of computer science disciplines because of their well-organized structure and effective search capabilities.

AVL Tree:

An AVL tree is a particular kind of self-balancing Binary Search Tree (BST) that makes sure that for every node, the balance factor—that is, the height difference between the left and right subtrees—does not exceed one. One important idea is the balance factor, which measures the tree's capacity to keep its equilibrium across insertion and deletion processes. Georgy Adelson-Velsky and Evgenii Landis presented the feature that sets apart AVL trees from conventional BSTs in their 1962 paper titled "An algorithm for the organization of information," which also gave rise to the tree's name. By maintaining a somewhat balanced tree, the self-balancing feature of the AVL tree optimizes search, insertion, and deletion processes.

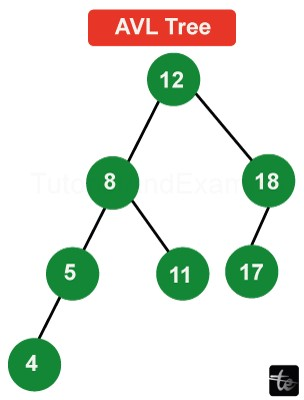
Applications of AVL Tree:

Databases use AVL trees for indexing, file systems for effective directory structures, compilers for managing symbol tables, and networking for optimizing routing tables. Their adaptability across multiple domains is demonstrated by their use in memory management, GIS applications, caching methods, and priority queues. Because of their ability to self-balance, AVL trees are useful in situations where maintaining ideal tree balance is essential because they enable quick and dependable search, insertion, and deletion operations.

B-Trees: Efficient Data Handling for Large Datasets

Large data sets are difficult for traditional binary search trees to handle well, which can cause problems with memory utilization and efficiency. The B-Tree is a flexible data structure that was created to overcome these restrictions. B-trees, also referred to as Balanced Trees, are notable for their ease of handling large amounts of data.

When compared to traditional binary search trees, B-trees stand out because they can hold multiple keys in a single node, which is why they are called "large key" trees. Because of this special characteristic, every node in a B-tree can hold many keys, which raises the branching factor and, as a result, lowers the height of the tree. Because of the lower height, less disk input/output is required, which speeds up search and insertion times. B-Trees work especially well with storage systems like CD-ROMs, flash memory, and hard drives that have large amounts of data to access slowly.

Most importantly, B-trees preserve equilibrium by ensuring that each node keeps a minimum number of keys. This balance ensures that, regardless of the starting tree structure, operations such as insertion, deletion, and searching always have a temporal complexity of O(log n).

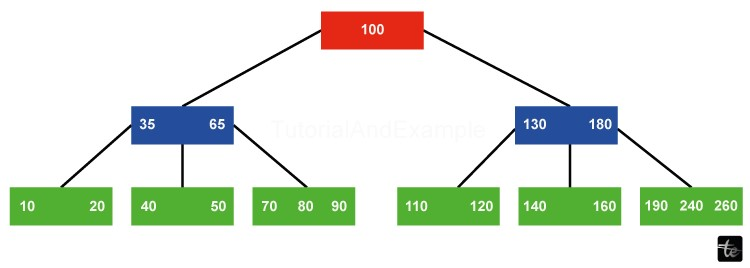
Features of B-Trees:

Uniform Leaf Level:

A balanced structure is ensured by the level placement of every leaf in a B-Tree.

Minimum 't' Degree:

A B-Tree has a minimum degree, represented by the letter "t," the value of which varies according to the size of the disk block.

Key Requirements for Nodes:

Each non-root node needs to have at least (t-1) keys, while the root can have at least 1 key.

The maximum number of keys for any node, including the root, is (2*t – 1).

How many children are there:

A node has as many offspring as the total number of keys it contains plus one.

Sorted Key Order:

Every key in a node is arranged in ascending order, and every key that falls between any two keys is included in the child between those two keys.

Complexity of Operation Time:

Like other balanced Binary Search Trees, B-Trees have an O(log n) time complexity for insert, remove, and search operations.

Insertion of Nodes:

A B-Tree differs from Binary Search Trees in that nodes are added primarily at leaf nodes, allowing for downward growth.

B-Tree Traversal: Navigating the Hierarchical Structure

A B-Tree's traversal pattern is similar to a Binary Tree's in order traversal. Starting with the leftmost child, the process methodically prints the leftmost child before repeating the process with the other children and keys. Finally, the traverse prints the rightmost child recursively to end the process. This method guarantees a systematic investigation of the B-Tree structure, enabling a thorough and structured analysis of its keys and nodes.

Search Operation in B-Tree:

In a B-Tree, the search process starts at its root, where keys are examined to determine if they include the desired key. If it is found, the search can be considered successful. Otherwise, the search starts again until either the target key is found or proved to be missing, strolling through a relevant child node based on ranges of keys. The balanced nature of the B-Tree makes it very efficient in processing large datasets, ensuring logarithmic search complexity (O(log n)).

#include <iostream>

const int MAX_KEYS = 3;   // The maximum number of keys that a node can hold.

Const int MAX_CHILDREN = 4; // The maximum number of children for an internal node

struct Node {

    int n;                 // The number of keys that are currently in the node

    int key[MAX_KEYS];     // An array to store the keys

    Node* child[MAX_CHILDREN]; // Array for storing the pointers to the children

    bool leaf;             // Specifies whether the node is a leaf in the tree

    // Constructor to initialize a node

    Node(int _n = 0, bool _leaf = true) : n(_n), leaf(_leaf) {

        for (int i = 0; i < MAX_KEYS; ++i) {

            key[i] = 0;

        }

        for (int i = 0; i < MAX_CHILDREN; ++i) {

            child[i] = nullptr;

        }

    }

};

Node* BtreeSearch(Node* x, int k) {

    int i = 0;

    // Locate the key in this node.

    while (i < x->n && k > x->key[i]) {

        ++i;

    }

    // Return the node if the key is found

    if (i < x->n && k == x->key[i]) {

        return x;

    }

    // If the given node is a leaf and the key cannot be found, return nullptr

    if (x->leaf) {

        return nullptr;

    }

    // Recursively search in the correct offspring node.

    return BtreeSearch(x->child[i], k);

}

int main() {

    // Usage example

    // Create and populate an exemplary B-Tree

    Node* root = new Node(1, true);

    root->key[0] = 10;

    // Look up the key 10 in the B-Tree

    Node* result = BtreeSearch(root, 10);

    // Output the result

    if (result) {

        std::cout << "Key 10 found in the B-Tree." << std::endl;

    } else {

        std::cout << "Key 10 not found in the B-Tree." << std::endl;

    }

    return 0;

}

Output:

Applications of B-Tree:

The uses of B-Trees in computer science and data management are very many. They are used in file systems to organize directories and ensure fast file operations. Thus, B-Trees are indispensable for database indexing because they allow a quick lookup of records and also enable better query execution. The balanced structure makes them perfect for use in work such as file system cache management, concurrency control of databases, GIS spatial indexing, and network routing tables. In addition, B-Trees are applicable to handling memory management systems for the efficient allocation and deallocation of block memories as well as serving web servers in managing session data. B-trees are a fundamental data structure in most computing fields; they can process huge databases with ease.

In conclusion, C++ tree data structures offer a very powerful and flexible way of handling hierarchical relationships through various computer programs. These architectures provide efficient solutions for the job such as searching, insertion, and also deletion, no matter if they are performed by binary trees, AVL-trees B – Trees, or any other versions. The natural branching and balance of the trees make them very useful in database management, filesystem organization, or network routing. Being object-oriented, C++ allows for easier tree structuring that enables the writing of reliable and modular programs. The tree data structures in C++ allow programmers to come up with many creative and effective solutions for a wide range of computation issues, showing that the trees are still very useful even after many decades since their introduction into computer science.