Stack Data Structure
The stack is a non-primitive and linear data structure. It works on the principle of LIFO (Last In First Out). That is, the element that is added to the end is removed first, and the element that is added first is removed at the end. There is only one end to insert and remove the element in the stack called the top end.
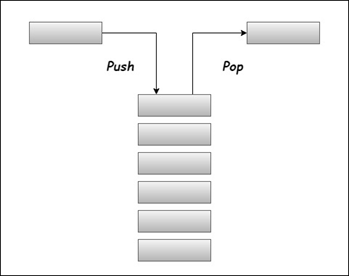
Example:
A good real-life example of a stack is the pile of dinner plates. When you have to take one plate from a pile, you pick the topmost plate and then the next plate. The last plate is picked at the end, which is placed first in a pile. The last plate is known as the base plate in the stack.

Stack operations
There are four types of operations in the stack.
- Push
- Pop
- Peek
- Update
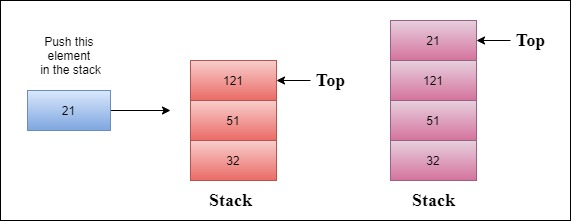
Push: Push operation is used to insert a new element in the stack. Push operation is shown in the figure below.
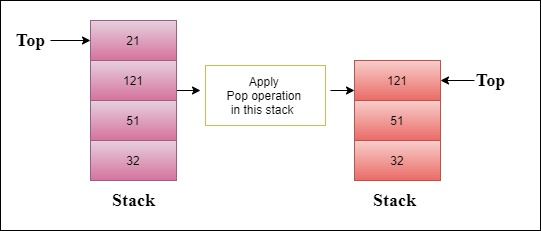
Pop: Pop operation is used to delete an element in the stack. Pop operation is shown in the figure below.
Peek: When the data is received from a particular location in the stack, that operation is called peep operation.
Update: When the value of an element is changed in the stack, that operation is called update operation.
Overflow & Underflow Conditions
If the stack is empty and trying to delete an element from it, that situation is called underflow. If the stack is full and trying to add a new element to it, that situation is called overflow.
Applications of stack
- Expression evaluation: Stack is used to evaluating the prefix, postfix, and infix expressions.
| Infix notation | Prefix notation | Postfix notation |
| A + B | + A B | A B + |
| (A - C) * B | *- A C B | A C – B * |
| A + (B * C) | + A * BC | A B C * + |
| (A + B) / (C + D) | / + A B – C D | A B + C D - / |
| (A + (B * D)) / (C - (D * B)) | / + A * B C – C * D B | A B C * + C D B * - / |
- Expression conversion: An expression is represented in the prefix, postfix, or infix notation. The stack is used to convert the form of one expression to another form.
- Syntax parsing: Many compilers use the stack to parsing the syntax expressions.
- Memory management: It is also used in memory management.
- Variable tracking: Stack is also used to track local variables in runtime.
- Parenthesis checking: Stack is also used to check whether parenthesis is correctly open and closed or not.
- String reverse: Stack is also used to reverse the string. In the string, we push the characters into the stack one by one and then pop the characters from the stack one by one.
- Undo: Stack is also used to undo in text-editor.
Implementation in C language
#include <stdio.h>
#include <stdlib.h>
#define MAX 10
int count = 0; // Creating a stack struct stack
{
int items[MAX];
int top; };
typedef struct stack st;
void createEmptyStack(st *s)
{
s->top = -1; } // Check if the stack is full int isfull(st *s)
{ if (s->top == MAX - 1)
return 1;
else
return 0;
} // Check if the stack is empty int isempty(st *s)
{
if (s->top == -1) return 1;
else
return 0; } // Add elements into stack
void push(st *s, int newitem)
{ if (isfull(s))
{
printf("STACK FULL");
}
else
{
s->top++; s->items[s->top] = newitem;
}
count++;
} // Remove element from stack
void pop(st *s)
{
if (isempty(s))
{
printf("\n STACK EMPTY \n");
}
else
{
printf("Item popped= %d", s->items[s->top]); s->top--;
} count--;
printf("\n");
} // Print elements of stack void printStack(st *s)
{
printf("Stack: ");
for (int i = 0; i < count; i++)
{
printf("%d ", s->items[i]);
}
printf("\n");
}
// Driver code int main()
{
int ch;
st *s = (st *)malloc(sizeof(st));
createEmptyStack(s);
push(s, 1);
push(s, 3);
push(s, 4);
printStack(s);
pop(s);
printf("\nAfter popping out\n");
printStack(s);
}