Graph Data Structure
A graph is a non-primitive and non-linear data structure. It is a group of (V, E) where V is a set of vertexes, and E is a set of edge. In the graph, a vertex is connected with another vertex, and the connection between two vertexes is called edge. Edge acts as a communication link between two vertexes. A graph is shown in the figure below.
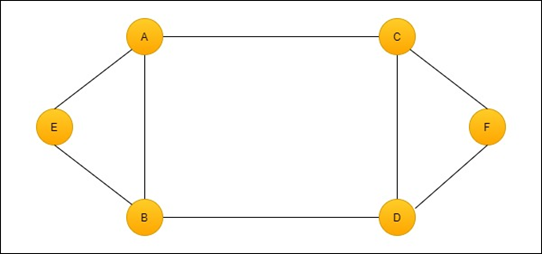
Where, V = {A, B, C, D, E, F}
E = {(AB), (AC), (AE), (BE), (BD), (CD), (CF), (DF)}
Types of Graph
Directed graph: A directed graph is a graph in which the edges have any direction, and such type of edge is called a directed edge. Directed edges are also called arcs. In a graph, edges are represented by a line, and the directed graph at each line has an arrow mark. The figure of the directed graph is shown below.
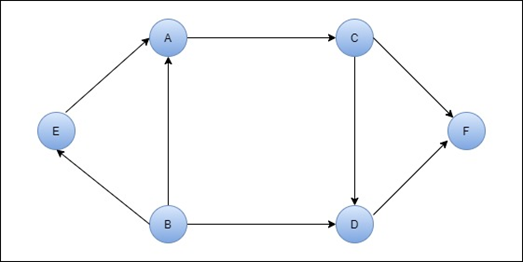
Undirected graph: An undirected graph is a graph in which the edges have not any direction. That is, there is no arrow mark in it. If an edge exists between the vertex A and B in the undirected graph, then the vertices can be traversed from both directions. The figure of the undirected graph is shown below.
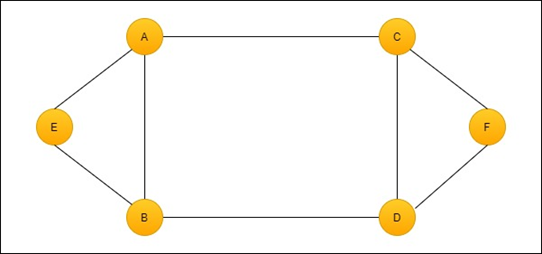
Terminology of graph
Weighted graph: A weighted graph is a graph in which edges are assigned some weights (value). These weights are real numbers. In other words, weight is the distance between one node to another.
Unweighted graph: An unweighted graph is a graph that does not have the weight (value) of the edges.
DAG: DAG stands for the directed acyclic graph. DAG is a directed graph that contains no cycles.
Multigraph: Multigraph is an undirected graph in which multiple edges are allowed in a single vertex.
Complete graph: A complete graph is a graph in which all nodes are linked with each other. A complete graph contains n(n-1)/2 edges. Where n is the number of the vertex.
Graph traversal
Graph traversal means visiting each vertex of the graph. There are several ways to visit the vertices of a graph. There are two types of graph traversal.
- BFS (Breadth first search)
- DFS (Depth first search)
Breadth first search
BFS is an algorithm for traversing and searching the graph data structures. It is used to find the shortest path in the graph and solve puzzle games. In the data structure, the queue is used to implement BFS.
In BFS, any one node is first visited, and then the nodes adjacent to it are visited. After this, all adjacent nodes of these adjacent nodes are also visited. And this process continues until all nodes have been visited.
Algorithm of BFS
Step 1. SET STATUS = 1 (ready state) for each node in G. Step 2. Enqueue the starting node A, and set its STATUS = 2 (waiting state). Step 3. Repeat Steps 4 and 5 until QUEUE is empty. Step 4. Dequeue a node N. Process it and set its STATUS = 3 (processed state). Step 5. Enqueue all the neighbors of N that are in the ready state (whose STATUS = 1) and set their STATUS = 2 (waiting state). [END OF LOOP]. Step 6. EXIT.
Depth first search
DFS is also an algorithm for traversing and searching graph data structures like BFS. In the data structure, the stack is used to implement DFS. DFS is a recursive algorithm that works on the principle of backtracking. DFS is used to analyze networks, map routes, and solve other computer science problems.
Algorithm of DFS
Step 1. SET STATUS = 1 (ready state) for each node in G. Step 2. Push the starting node A on the stack and set its STATUS = 2 (waiting state). Step 3. Repeat Steps 4 and 5 until STACK is empty. Step 4. Pop the top node N. Process it and set its STATUS = 3 (processed state). Step 5. Push on the stack all the neighbours of N that are in the ready state (whose STATUS = 1) and set their. STATUS = 2 (waiting state) [END OF LOOP] Step 6. EXIT.