Traversal of binary tree

Traversal of binary tree: A node is visited only once in the traversal of the binary tree. There are three main types of traversal methods in the binary tree.

1. In-order traversal
2. Pre-order traversal
3. Post-order traversal

In-order traversal: 

In the in-order traversal method, the left child and left subtree are traversed first, afterward the root tree and then the right children or the right subtree are traversed.

Algorithm of In-order traversal

In-order-traversal (tree)
Step 1: Start with left sub-tree      // call In-order (left subtree) 
Step 2: Then, root tree 
Step 3: And then, right sub-tree    // call In-order (right subtree)

Example: Find the in-order traversal for this tree.

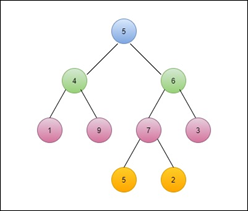
Solution.

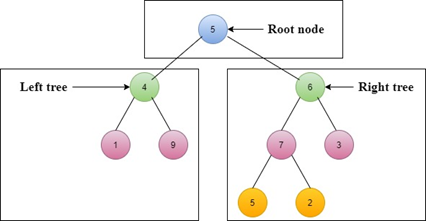
Step 1: Left sub-tree is 1 ? 4 ? 9

Step 2: Root node is 5

Step 3: Right sub-tree is 5 ? 7 ? 2 ? 6 ? 3    

In-order Traversal = 1 ? 4 ? 9 ? 5 ? 5 ? 7 ? 2 ? 6 ? 3

Pre-order Traversal:

In the pre-order traversal method, the root node is traversed first, then the left subtree, and then the right subtree is traversed.

Algorithm of pre-order traversal

Pre-order-traversal (tree) 
Step 1: Start with the root node    
Step 2: Then, the left sub-tree       // call Pre-order (left subtree) 
Step 3: And then, right sub-tree    // call Pre-order (right subtree)

Example: Find the pre-order traversal for this tree.

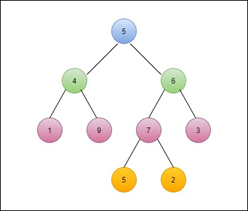
Solution.

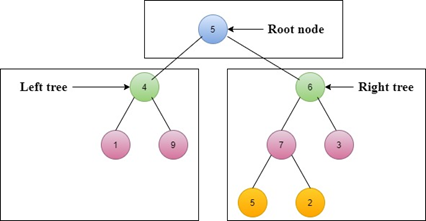
 Step 1: Root node is 5

Step 2: Left sub-tree is 4 ? 1 ? 9

Step 3: Right sub-tree is 6 ? 7 ? 5 ? 2 ? 3    

Pre-order Traversal = 5 ? 4 ? 1 ? 9 ? 6 ? 7 ? 5 ? 2 ? 3

Post-order traversal:

In the post-order traversal method, the left child and left subtree are traversed first, then the right subtree is traversed, and then the root node.

Algorithm of Post-order traversal

Post-order-traversal (tree)
Step 1: Start with left sub-tree        // call Post-order (left subtree) 
Step 2: Then, right sub-tree           // call Post-order (right subtree) 
Step 3: And then, root tree

Example: Find the Post-order traversal for this tree.

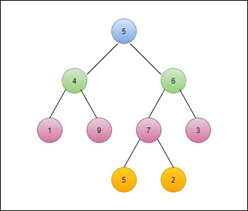
Solution.

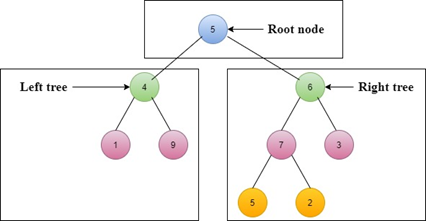
Step 1: Left sub-tree is 1 ? 9 ? 4
Step 2: Right sub-tree is 5 ? 2 ? 7 ? 3 ? 6
Step 3: Root node is 5    
Post-order Traversal = 1 ? 9 ? 4 ? 5 ? 2 ? 7 ? 3 ? 6 ? 5

Applications of binary tree

1. The binary search tree is used in many search applications.
2. Nowadays, a binary Space Partition is used for every 3D game.3.
3. The binary tree is used in every high bandwidth router that stores the router table.

Binary tree program in C language

// Binary Tree in C   
#include <stdio.h> 
#include <stdlib.h>   
struct node 
{   
int data;   
struct node *left;   
struct node *right; 
}; 
struct node *newNode(int data) 
{   
struct node *node = (struct node *)malloc(sizeof(struct node));   
node->data = data;   node->left = NULL;   
node->right = NULL;   return (node); }   
void traversePreOrder(struct node *t)
 {  
 if (t != NULL) 
  {   
  printf(" %d", t->data);  
   traversePreOrder(t->left); 
    traversePreOrder(t->right); 
  } 
}  
 void traverseInOrder(struct node *t)
 {  
 if (t != NULL) 
  {    
 traverseInOrder(t->left); 
    printf(" %d", t->data);  
   traverseInOrder(t->right);
  }
 } 
  void traversePostOrder(struct node *t)
 {  
 if (t != NULL) 
  {    
 traversePostOrder(t->left); 
    traversePostOrder(t->right); 
    printf(" %d", t->data); 
  } 
}   
int main() 
{  
 struct node *root = newNode(1); 
  root->left = newNode(2);  
 root->right = newNode(3); 
  root->left->left = newNode(4); 
  printf("The preorder traversal of the tree is: "); 
  traversePreOrder(root);   
printf("\nThe inorder traversal of the tree is: "); 
  traverseInOrder(root);   
printf("\nThe postorder traversal of the tree is: ");  
 traversePostOrder(root); }