Python Matrix Multiplication

One of the most fundamental mathematical structures, matrices are used often in many disciplines, including mathematics, physics, engineering, computer science, etc.

For example, matrices and associated operations (multiplication and addition) are commonly used in deep learning and related statistical tasks to generate predictions based on inputs.

When two matrices of dimensions (a x b) and (b x c) are multiplied, the third matrix of dimension (a, c), known as the product matrix, is created as a result. This binary operation was initially introduced in 1812 by Jacques Binet.

The process for multiplying two matrices is described below. The process for multiplying two matrices is fairly straightforward, despite its apparent complexity.

To get the Two Matrices A and B's Product, or AB

• Make sure that the first matrix, A, has the same number of rows as the number of columns of the second matrix, B. In other words, they must have dimensions that take the forms (a x b) and (b x c), respectively. The matrices cannot be multiplied if that is not the case.

• Create a blank product matrix in C.
• For each i and j, repeat the following, 0<=i<a, 0<=j<b:
  • Take the ith row from A and the jth row from B. The components that are all present at the same index should be added together. For example, multiplying the first element of the ith row by the first element of the jth column, and so forth.
  • Consider the total of the items that were calculated in the previous phase.
  • Put this total in the [i, j] cell of the product matrix C.
• As a final check, confirm that the generated product matrix has dimensions (a x c).
  
  Multiplication of matrices is not commutative. That is to say, AB and BA are not always equal. Additionally, it is frequently conceivable that only one or none of these items are defined.

Implementation of Code With the Use of Nested Loops

The easiest and slowest way to put the matrix multiplication program into action is through nested loops. Generally speaking, the outer loop iterates over each row of the first matrix, the second loop, which is included inside the first loop, iterates over each column of the second matrix, and the operation required to evaluate C[i][j] for a summation is carried out in the third loop.

Algorithm

1. The matrix dimensions should be saved in several variables.
2. Examine whether the matrices can be multiplied or not. If not, stop the program; if yes, go ahead.
3. Utilize an index-variable I to iterate across the rows of matrix A.
4. Use the index-variable j to iterate through the columns of matrix B inside the first loop.
5. Set the variable curr_val to 0 now.
6. Create a second loop using the variable k that iterates through the column dimension of A (or the row dimension of B).
7. For each iteration of the innermost loop, add the value of A[i][k] x B[k][j] to the variable curr_val.
8. Assign the value of curr_val to C[i][j] for each iteration of the innermost loop.

Code:

A = [[5,6,7],[1,3,2],[4,9,8]]
B = [[12,8],[9,5],[8,13]]
p = len(A)
q = len(A[0]) # retrieving the sizes/dimensions of the matrices
t = len(B)
r = len(B[0])
if(q!=t):
   print("Matrix sizes are not suitable, Error!")
   quit()
C = []
for row in range(p):
   curr_row = []
   for col in range(r):
       curr_row.append(0)
   C.append(curr_row)
for i in range(p): # performing the matrix multiplication
  for j in range(r):
       curr_val = 0
       for k in range(q):
           curr_val += A[i][k]*B[k][j]
       C[i][j] = curr_val
print(C)

output:

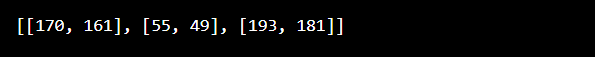
With the use of List Comprehensions

Python's list comprehensions provide a clearer and easier comprehending way to make lists from other iterables like lists, tuples, strings, etc. Two subexpressions make up the list comprehension statement:

1. The first sub-expression determines what will be displayed in the list (for example, some transformation, such as increment by 1, on each element of the iterable).
2. The second portion is responsible for obtaining the data from the iterable so that the first section can act upon, alter, or analyze it. One or more for statements combined with zero or more if statements make up the second section.

zip() function in Python

The zip() function, in its simplest form, is used to index-based group and ungroup the data supplied as iterables (such as lists, tuples, strings, list of strings, etc.).

For example, let's say that during packing, all of the data present at index 0 across all of the input iterables will be merged into a single tuple, then the data at index 1 and another tuple, and so on. Then, a zip object representing the entirety of these tuples is returned. Unpacking is the opposite of this operation. For a better understanding, go to the code examples.

Example: The Packing Operation

Code:

m = [[10,1,6],[7,4,9],[11,3,2]]
m1 = ["arpita", "namrita", "akshita"]
re = zip(m, m1)
print("The data type of res is: ",type(re))
print("The contents of res are:",list(re))

Output:

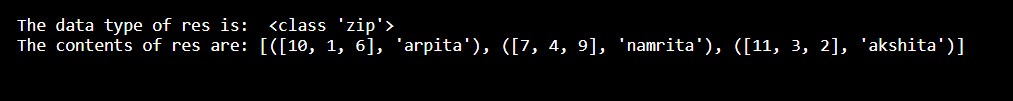
Example: The unpacking operation

Code:

A = [[4,6],[15,7],[9,10]]
re = zip(*A)
print("The data type of res is: ",type(re))
print("The contents of res are:",list(re))

Output:

Numpy Library for Matrix Multiplication

A huge number of high-level mathematical functions are available in the NumPy Python library, which is highly optimized to conduct calculations on massive, multi-dimensional arrays and matrices. Thus, it should not be a surprise that it offers some capability for a fundamental matrix operation like multiplication.

We will go through the following three methods from the Numpy library that are pertinent to matrix multiplication:

1. numpy.matmul() method or the “@” operator
2. numpy.dot()
3. numpy.multiply() method

Additionally, Numpy offers a few techniques that apply to vector multiplications.

It's crucial to keep in mind that all of the NumPy module's functions are vectorized during implementation, making them significantly more effective than pure Python loops. Anywhere you can attempt to substitute them for several for-loops.

numpy.matmul() or “@” operator

The product matrix is directly returned by the matmul() method, which accepts two matrices that can be multiplied. The operands must either already be of the type numpy.array or be explicitly typecast to that type for you to utilize the "@" symbol.

The methods above are represented by the code below:

import numpy as np


A = [[3,1,2],[10,3,4],[6,9,7]]
B = [[4,3],[14,8],[4,15]]
C1 = np.matmul(A, B)
C2 = np.array(A)@np.array(B)
 print(type(C1))
print(type(C2))
 assert((C1==C2).all())
print(C1)

Output:

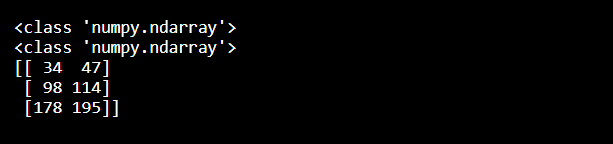
numpy.dot() Method

Based on the input parameters, this method offers a variety of behaviours and use cases, but it is advised that it only be used when we need the dot product of two 1D vectors.

Let's take a glance at the documentation: a two arrays dot product, Specifically,

1.     If both a and b are 1-D arrays, it is the inner product of the vectors (without complex conjugation)

2.     Although using matmul or a @ b is advised, matrix multiplication is possible if both a and b are 2-D arrays.

3.     It is equal to multiplying and using numpy if either an or b is 0-D (scalar). It is preferable to use multiply(a, b) or a*b.

Note: Both numpy.matmul() and numpy.dot() produce the same outcome for 2D matrices. Their responses vary because higher dimension matrix multiplication is involved.

Let's examine two approaches to using np.dot to code our matrix multiplication application ():

Example:

import numpy as np


A = [[3,1,2],[10,3,4],[6,9,7]]
B = [[4,3],[14,8],[4,15]]
C1 = np.matmul(A, B)
C2 = np.array(A)@np.array(B)
 print(type(C1))
print(type(C2))
 assert((C1==C2).all())
print(C1)

Output:

You'll see that we used the assert statement once more to verify that C1 and C2 are equal matrices, cross-validating our assertion that they behave identically for 2D arrays. Here, we've discovered yet another approach for using the numpy.dot() method to determine the product of matrices A and B.

Example:

import numpy as np
A = [[12,1,4],[9,3,4],[6,5,11]]
B = [[6,4],[15,4],[8,12]]
D = list(zip(*B))
C = [[0 for _ in range(2)] for _ in range(3)]


for i in range(3):
   for j in range(2):
       C[i][j] = np.dot(A[i], D[j])
print(type(C))
print(C)

Output:]

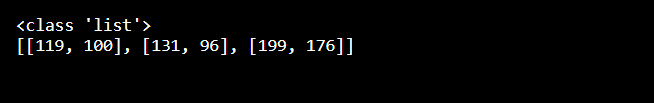
• Take note of the type of matrices they produce, even if the resultant matrices in the first and second code samples have the same cell values.
• The second method takes advantage of C[i][j], the dot product of the ith row of A and the jth column of B, is.

The np.multiply method is the last technique worth addressing, even if it has little to do with our subject.

C. numpy.multiply()

The standard matrix multiplication step is not taken by this technique (refer to the code examples). This technique only functions when the operands are ;

1. Scalar and a matrix
2. Two matrices with the same dimensions

According to the output C of the code presented below, this method multiplies the scalar with each matrix element in the first situation.

In the second case, this approach is used to compute the Hadamard Product, a matrix composed of the element-wise products of two matrices, A and B. In other words, C[i][j] = A[i][j]*B[i][j] for all possible values of I and j, where C is the Hadamard product matrix.

Any other scenario will lead to a mistake.

Code:

x = [[1,2,3],[4,5,6],[7,8,8]]
y = [[2,3,4],[7,5,3],[1,4,2]]


# case 1
A = np.multiply(3, x)
# case 2
B = np.multiply(x, y)


print("C = ", A)
print("D = ", B)

Output:

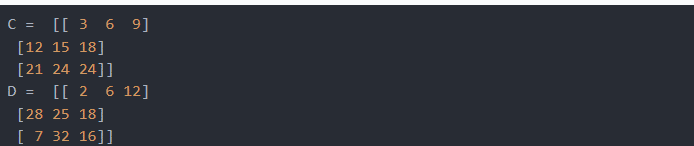
• It's also interesting to notice that the np.multiply() action can be replaced with the "*" operator, just like the np.dot() operation can. However, the operands, in this case, must also be NumPy array types or explicitly typecast into them.
• This operator will produce an error if this requirement is not met. To further understand its application, let's examine the code sample provided below:

Code:

x = [[1,2,3],[4,5,6],[7,8,8]]
y = [[2,3,4],[7,5,3],[1,4,2]]


z = 3*np.array(x)
j = np.array(x)*np.array(y)


print("C = ", z)
print("D = ", j)
Also take note that both outputs, C and D, continue to have the same numpy.ndarray.
print(type(z))
print(type(j))

Output:

Conclusion  

1. The product matrix is the result of the binary operation known as matrix multiplication, which is performed on two matrices.
2. Matrix multiplication is not commutative and can only be performed between compatible matrices.
3. To perform the matrix multiplication of matrices A and B in Python without using any built-in methods or library functions, we iterate over all the rows of matrix A and all the columns of matrix B and retrieve the total of their element-wise products.
4. We can eliminate the nested for loops by using Python's zip function, which allows us to do the same objective as previously with less code.
5. Unlike the nested loop method, list comprehension is still a practical way to multiply matrices in Python.
6. List comprehensions are typically quicker than the zip approach for creating lists, but not when computations are required.
7. The numpy library's methods, such as numpy.matmul(), numpy.dot(), and numpy.multiply() can multiply matrices in Python significantly more quickly.

These techniques are more effective because they employ vectorization, which speeds up their execution compared to Python's explicit for-loops.

It is advised to use NumPy library methods rather than developing your own code to multiply the matrices to produce clear, understandable code and make the application effective.