Permutations in Python
Recursion
Basic idea: for numbers of length N.
N-1 items are chosen at random between 0 and then generate permutations using the remaining N-1 elements in a recursive fashion. Once you've done that, add up your findings. The recursion code in Python will make this procedure easier to understand.
As an example, we may use swap(0-i),i in the range [0-1, 2...N-1] as an easy approach to pick up the values from num[0] to [N-1]. Below is an illustration of how this works:
OUTPUT
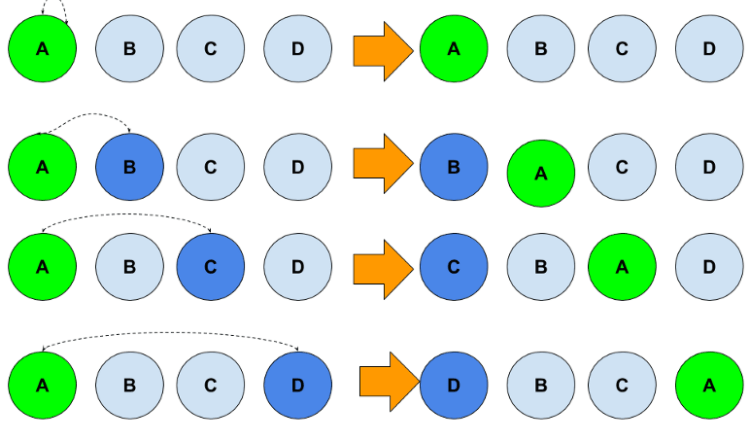
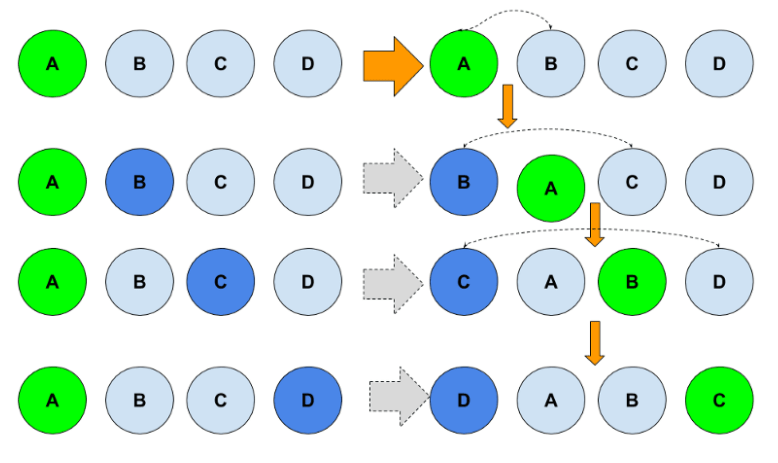
After a simple switch, the remaining values are no longer in the same order as they were before. To solve this problem, we may apply a better switching technique, as demonstrated in the updated image below:
OUTPUT
SYNTAX
/*
jimmy shen
02/20/2020
A code to implement the naive o(n^n) permutation algorithm.
runtime 12 ms
time complexity O(n!)
space complexity O(n) as we have temp
*/
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> res;
recursive_permute(nums, res, 0);
return res;
}
void recursive_permute(vector<int>&nums, vector<vector<int>> &res, int pos){
// if we reach the size of nums, we are done.
vector<int> temp = nums;
if(pos == temp.size()-1){
res.push_back(temp);
return;
}
else{
for(int i=pos; i<temp.size(); i++){
swap(temp[pos], temp[i]);
recursive_permute(temp, res, pos+1);
}
}
}
};
Backtracking
Here's a quick rundown of how it works:
I in [0,1,2] is swapped with I in the first layer. To demonstrate the concept, I'll use the index parameter in the swap function. It's swapped in the programme (nums[0], nums[i])
For the second layer, we'll start at the second position and work our way up to the first.
When we get to the leaf node or the bottom case, we go back to the previous node and continue on.
It's DFS with a little bit of backtracking. If you've never heard of DFS or backtracking, now is the time to learn about it. First, do some research on Google to have a better understanding of those ideas.
runtime
Runtime: 8 ms, faster than 98.91% of C++ online submissions for Permutations.
Memory Usage: 9.2 MB, less than 95.52% of C++ online submissions for Permutations.
SYNTAX
/*
jimmy shen
02/20/2020
A code to implement the naive o(n^n) permutation algorithm.
runtime 12 ms
time complexity O(n!)
space complexity O(1)
*/
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> res;
dfs(nums, res, 0);
return res;
}
void dfs(vector<int>&nums, vector<vector<int>> &res, int pos){
// if we reach the size of nums, we are done.
if(pos >= nums.size()){
res.push_back(nums);
return;
}
else{
for(int i=pos; i<nums.size(); i++){
swap(nums[pos], nums[i]);
dfs(nums, res, pos+1);
//recover the nums to do backtracking
swap(nums[pos], nums[i]);
}
}
}
};
When the pos equals nums.size-1, we are done, and since there is only one element remaining, swap is unnecessary. Because of this, the code below is functional as well.
SYNTAX
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> res;
dfs(nums, res, 0);
return res;
}
void dfs(vector<int>&nums, vector<vector<int>> &res, int pos){
// if we reach the size of nums, we are done.
if(pos == nums.size()-1){
res.push_back(nums);
return;
}
else{
for(int i=pos; i<nums.size(); i++){
swap(nums[pos], nums[i]);
dfs(nums, res, pos+1);
//recover the nums to do backtracking
swap(nums[pos], nums[i]);
}
}
}
};
Backtracking differs from recursion in several ways.
They're really similar, in essence. That's because recursion employs a DFS strategy to address the issue. When we return to the parent node after DFS, we switch back to ensure that future investigation of other branches starts from a valid starting point when we go back to the parent node. As a result, when we approach the end of the DFS search, we'll need to do another swap.
We don't need to switch back for the recursion. However, we copy the initial num to temp and do the recursion actions on the basis of that.
Although it appears to be quite comparable, the memory complexity of recursion is O(n), where n is the size of nums. O is the name of the backtracking letter (1).
Runtime: 36 ms, faster than 83.58% of Python3 online submissions for Permutations.
Memory Usage: 13 MB, less than 96.43% of Python3 online submissions for Permutations.
SYNTAX
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
def dfs(pos):
if pos==len(nums)-1:
# using deep copy here to harvest the result
res.append(nums[:])
for i in range(pos, len(nums)):
#swap
nums[pos], nums[i] = nums[i], nums[pos]
dfs(pos+1)
nums[pos], nums[i] = nums[i], nums[pos]
dfs(0)
return res