Python Modulo
For basic calculations, Python provides operators. Python supports a broad range of Arithmetic Operators to do arithmetic, as given below:
| + | Addition |
| * | Multiplication |
| - | Subtraction |
| / | Division |
| // | Floor division |
| ** | Exponentiation |
| % | Remainder/Modulus |
As you can see, one of these basic arithmetic operators is the modulo operator (%), which finds the modulus that is the remainder of its first operand relative to the second. In plain English, it yields the remainder of dividing the first operand by the second operand.
Syntax:
remainder=a%b
Where a and b are integers.
For Example:
25%6 evaluates to 1 since 6 goes into 25 four times with a remainder of 1.
Similarly,
6%2.5 will yield 1.0.
Note: Here, the operands can be of number types.
Python Modulo Operator Fundamentals
The modulo operator can be applied to numeric types like int and float and other types like math.fmod(), decimal.Decimal, just like any other arithmetic operator, and it’s not surprising that it can even be used with one's classes.
Usage of Modulo Operator (%) with one of the numeric Types‘int’:
The modulo operator (%) is most commonly used with one of the numeric types int, i.e., integers. The remainder of the ordinary Euclidean division is returned when the modulo operator is applied to two positive integers.
Python Modulus Operator Exception Case
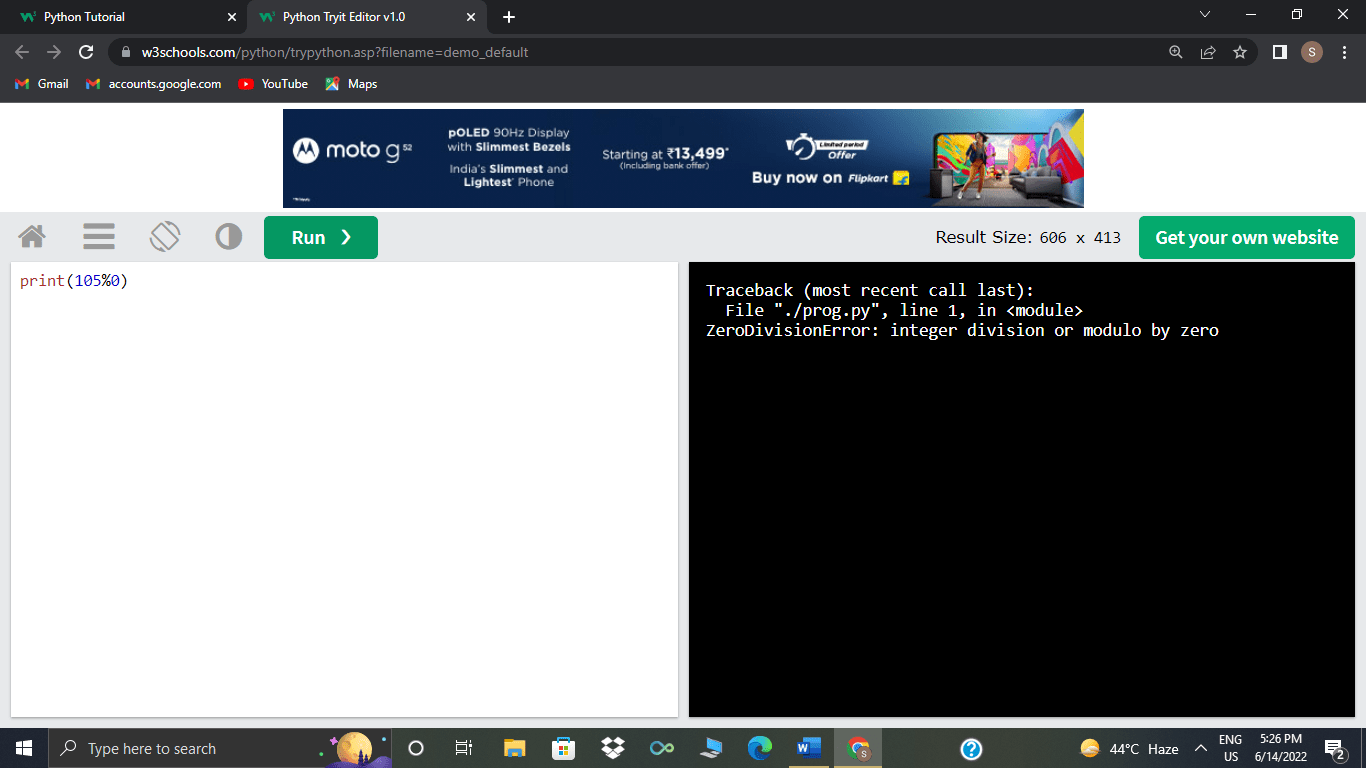
Python returns a ZeroDivisionError when one uses the modulo operator with a divisor of 0, just like the divisor operator(/).
For examples,
>>>6%3
>>>25%6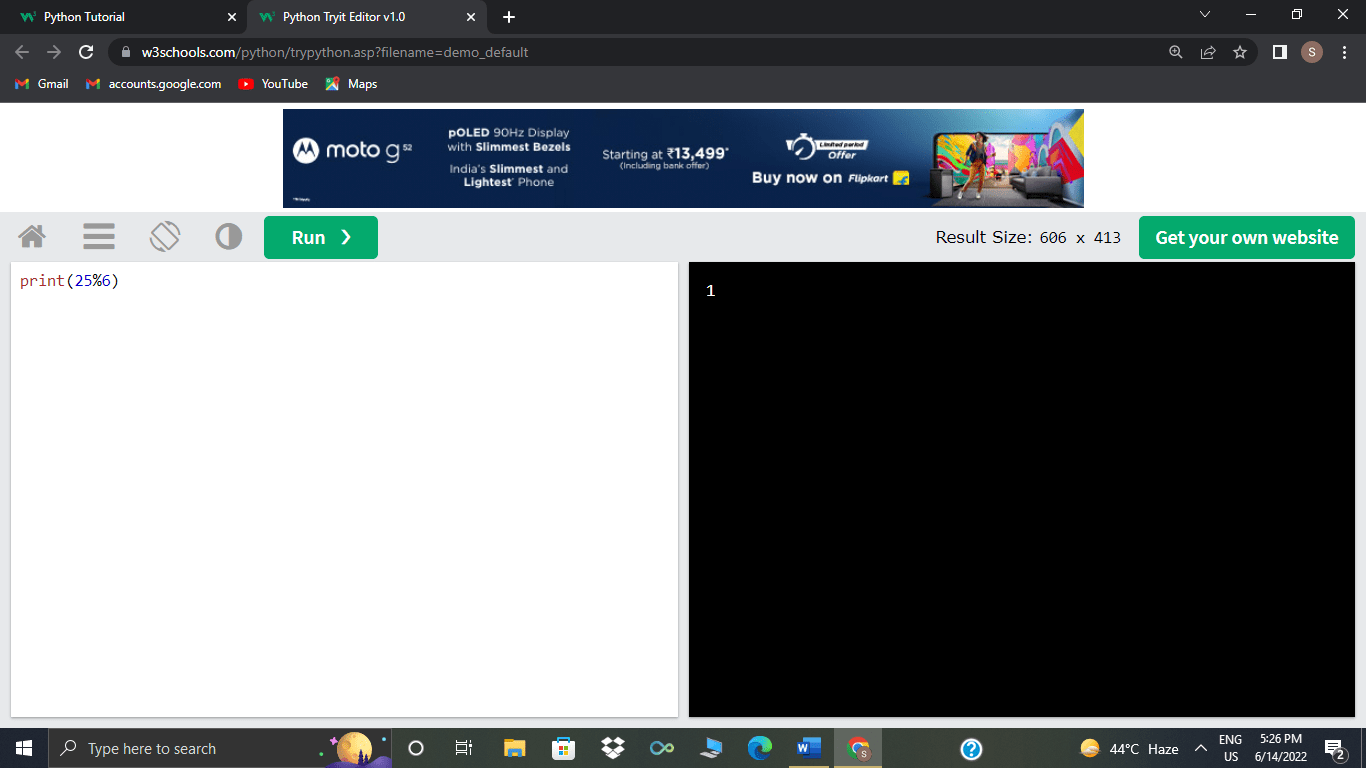
>>>105%0
Usage of Modulo Operator with Numeric Type ‘float’;
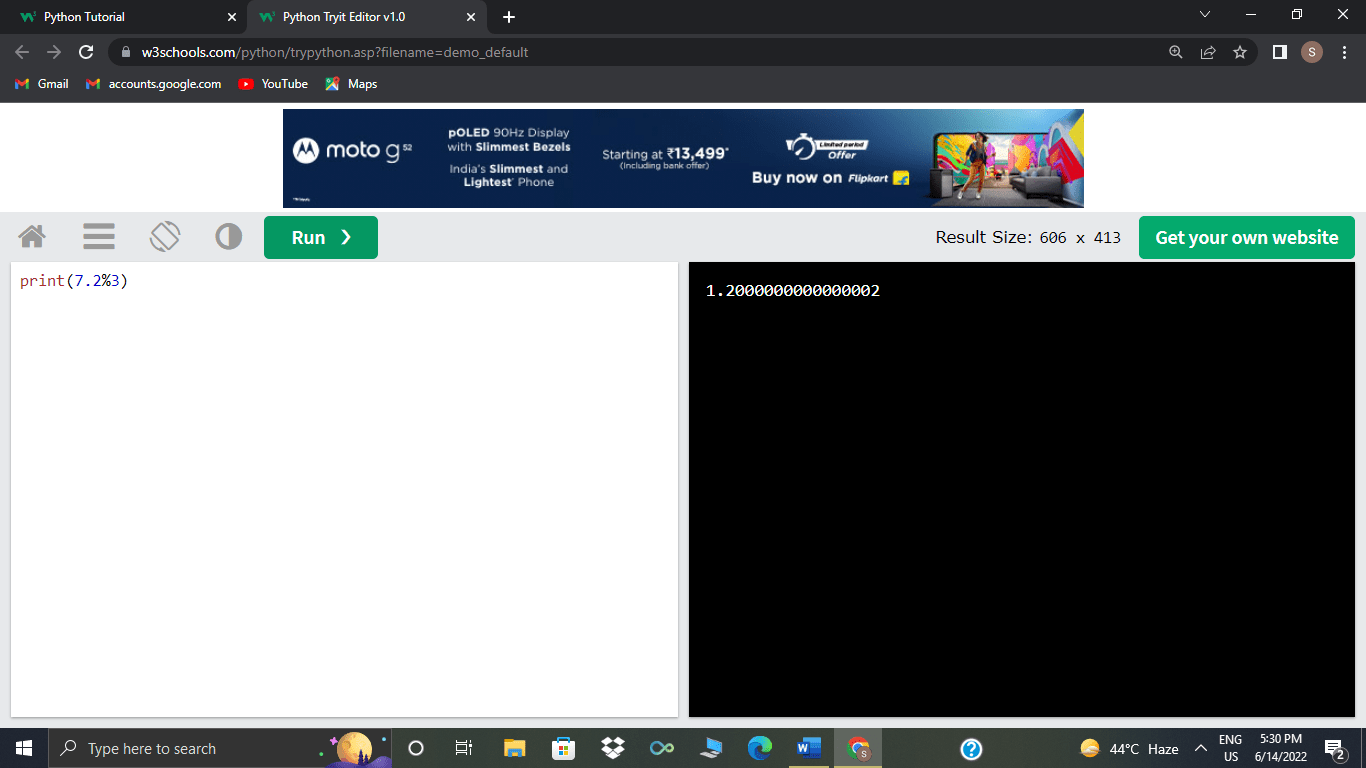
When the modulo operator is used with a float, it returns the remainder of the division just like in the case with int, but with a difference that the remainder will be a float value.
>>>7.2%3
Using a float with the modulo operator can quite work. Thus, Python provides a function to perform modulo operations on float values, and that function is The math.fmod(). (Do not forget to import math before using this function.)
>>> import math
>>>math.fmod(7.2,3)
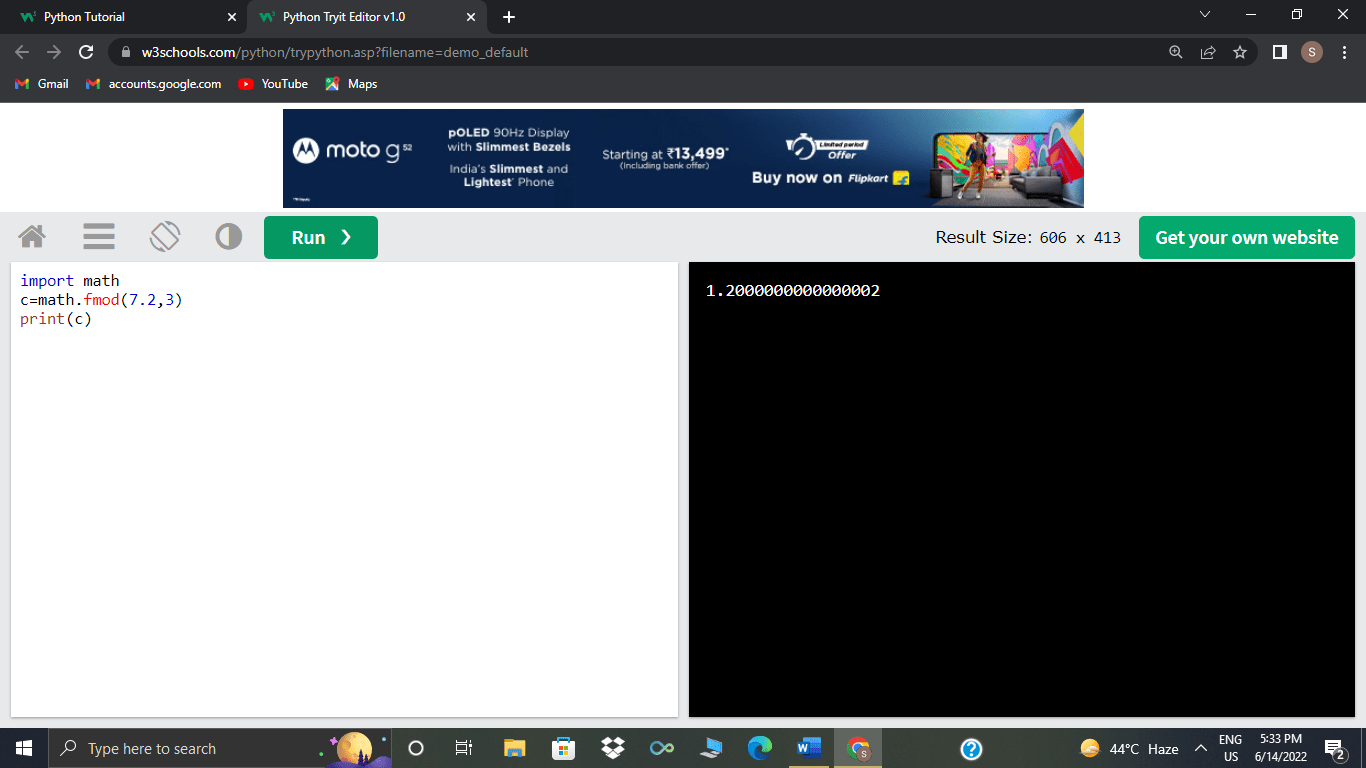
Suppose we briefly discuss the basic difference between the python modulo operator and math.fmod(), then this lies in how the outcome of the modulo operation is calculated by math.fmod(). One will encounter different results if using a negative operand between math.fmod(a, b) and a % b.
The math.fmod() and the modulo operator can make one face rounding and precision issues while dealing with floating-point arithmetic, as shown in the example below.
Using Modulo Operator with a Negative Operand
When two positive operands are used with the modulo operation(%), the result is predictable, and things stay simple. Still, when a negative operand is used, things become more complicated, contrary to the positive one’s case.
When using a modulo operator with a negative operand, whether the remainder must take the sign of the dividend (i.e. the number being divided) or the sign of the divisor (i.e. the number by which the dividend is being divided) is decided by the computer but the way by which computers decide it remains unclear as it rolls out. The fact is Different programming languages deal with this scenario in different ways.
If we talk in Python and some other languages, then the remainder will take up the sign of the divisor instead of the dividend, opposite to the case of JavaScript.
For example,
>>>9%-4
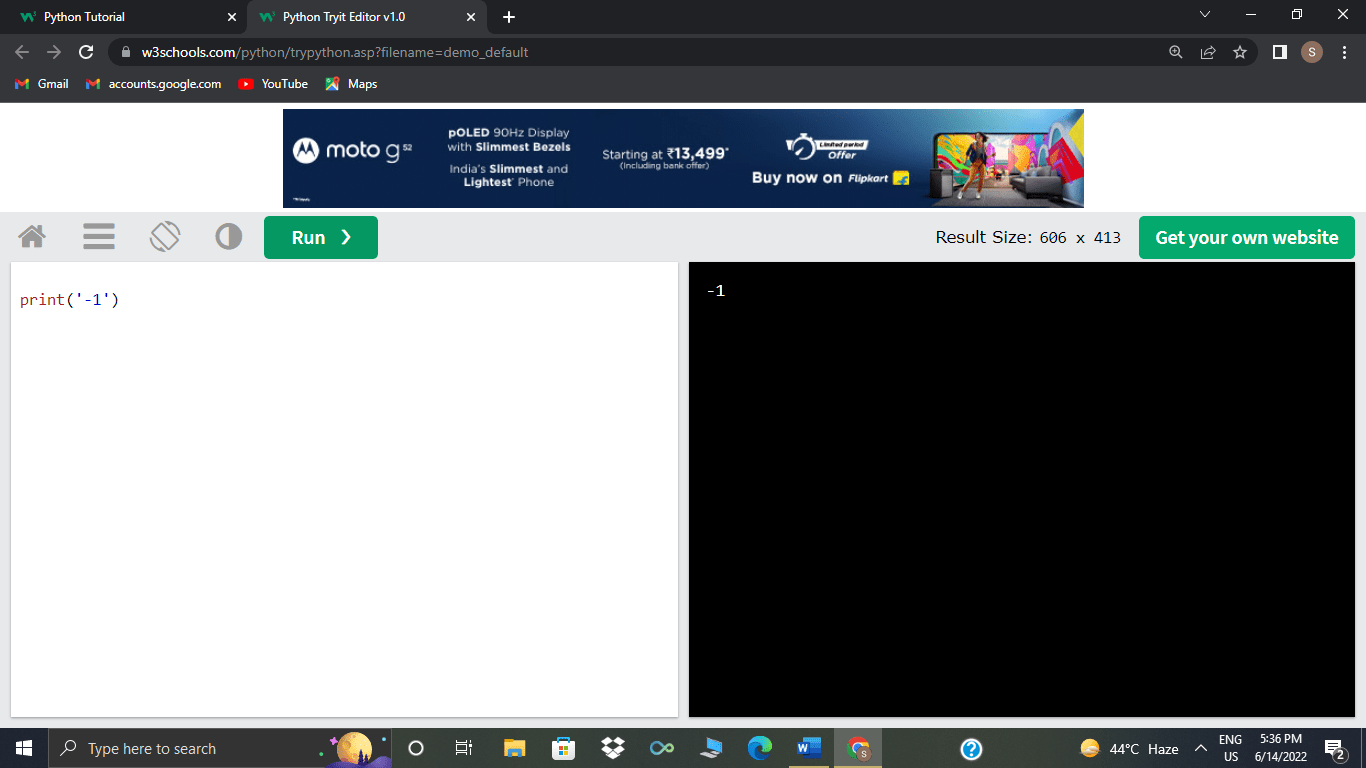
As you can see above, the remainder, i.e. here, in this case, is -1, takes the sign of the divisor, i.e. -4. The equation given below is used in Python and other languages where the remainder takes the divisor's sign instead of the dividend's:
r = a - (n * floor(a/n))The term floor() in this equation denotes the use of floor division.
One must understand that in Python, not all modulo operations are the same. At one place where the modulo used with the int and float types will take the sign of the divisor rather than the dividend; at the other place with other types will not.
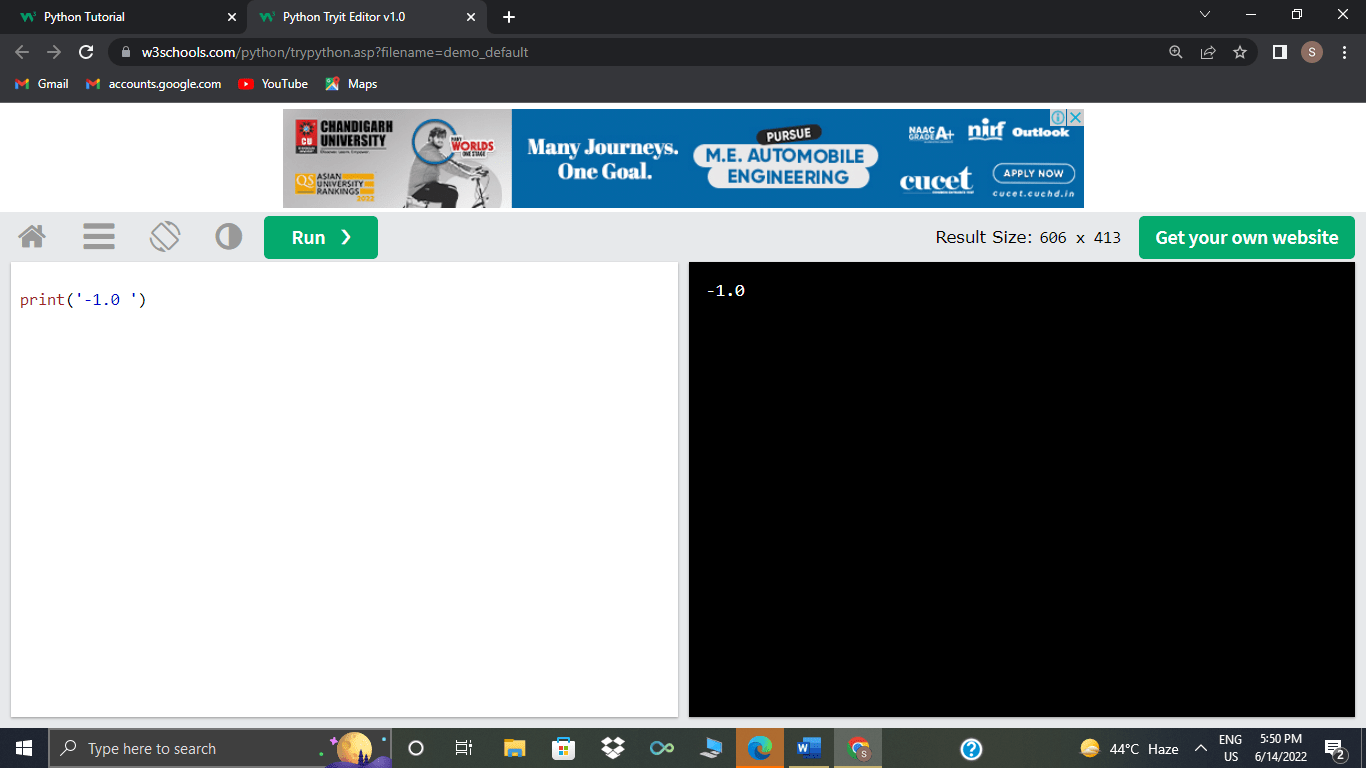
Take a look at an example of this below, where the results of two tests are compared i.e.10.0 % -3.0 and math.fmod(8.0, -3.0):
>>>10.0%-3.0
>>>Importmath
>>>math.fmod(10.0,-3.0)
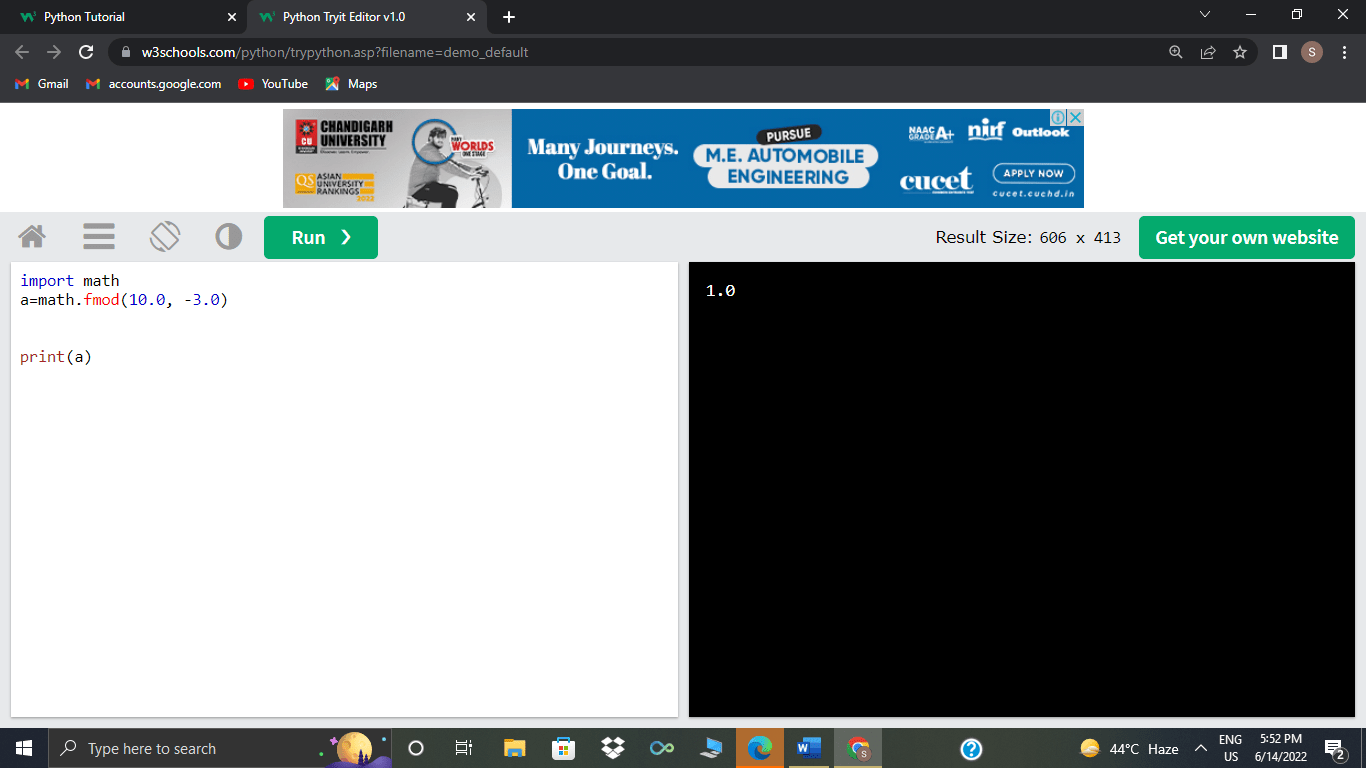
That math is now plainly understood. When employing truncated division, fmod() uses the sign of the dividend, whereas float uses the sign of the divisor.
The Modulo Operator and the divmod ()
Now let’s talk about divmod(), a built-in Python function. The divmod() uses the modulo operator internally. Two parameters are taken by divmod(), and then it returns a tuple containing the results of floor division(//) and modulo(%) using the given parameters, as shown in the example below;
>>>divmod(37,6)
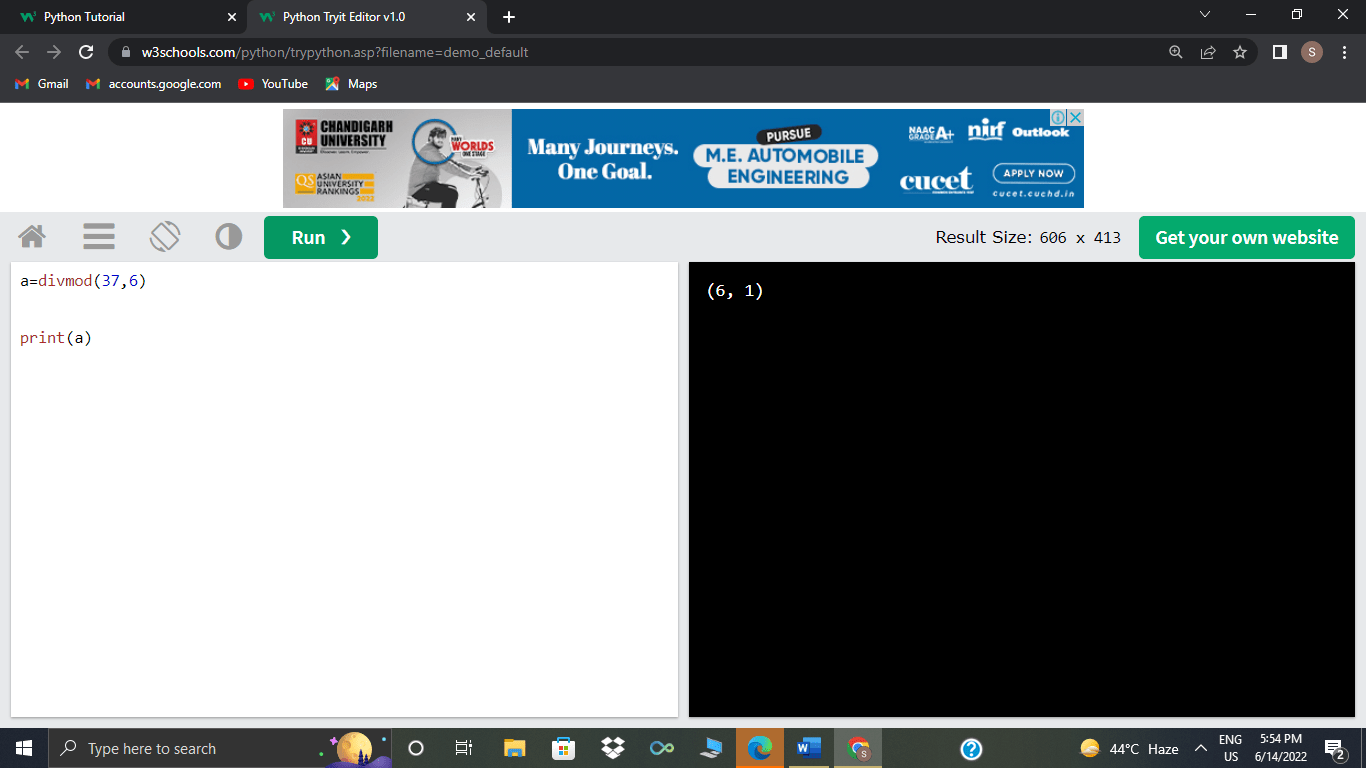
As you can see above, the two parameters taken by divmod() are 37 and 6, and after that, it returned a tuple(6,1) containing the results of floor division, i.e.37//6, that yields 6 and modulo i.e.37%6 that yields 1.
Now let’s move to an example where the second parameter taken would be negative.
>>>divmod(37, -6)
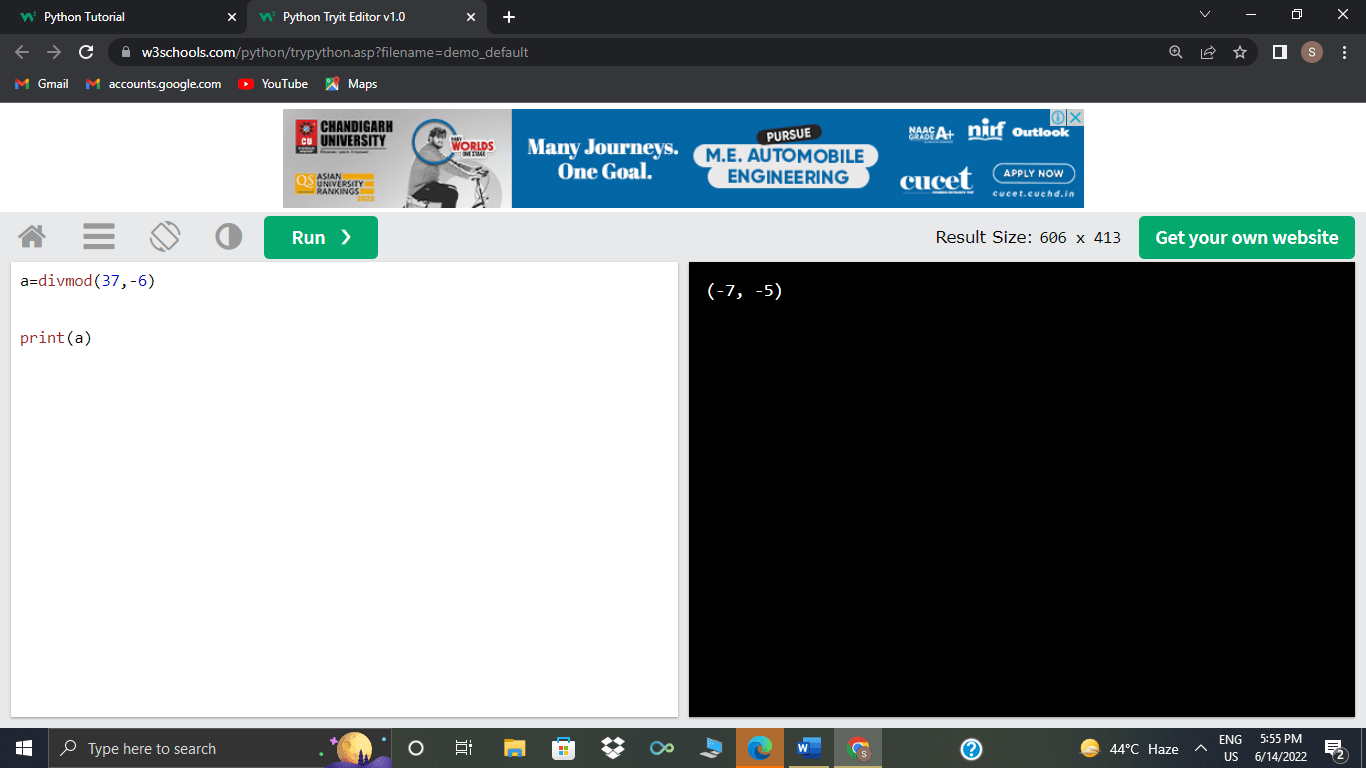
As already discussed, when negative int the modulo operator is used, the remainder takes up the sign of the divisor instead of the dividend.
Using the Modulo Operator in Python with decimal.Decimal
The modulo operator can be used with Decimal from the decimal module. Use decimal.Decimal if you wish to have more control over the precision of floating-point arithmetic operations. Now let’s see some examples of using integers(whole) with decimal.Decimal and the modulo operator(%):
Example:
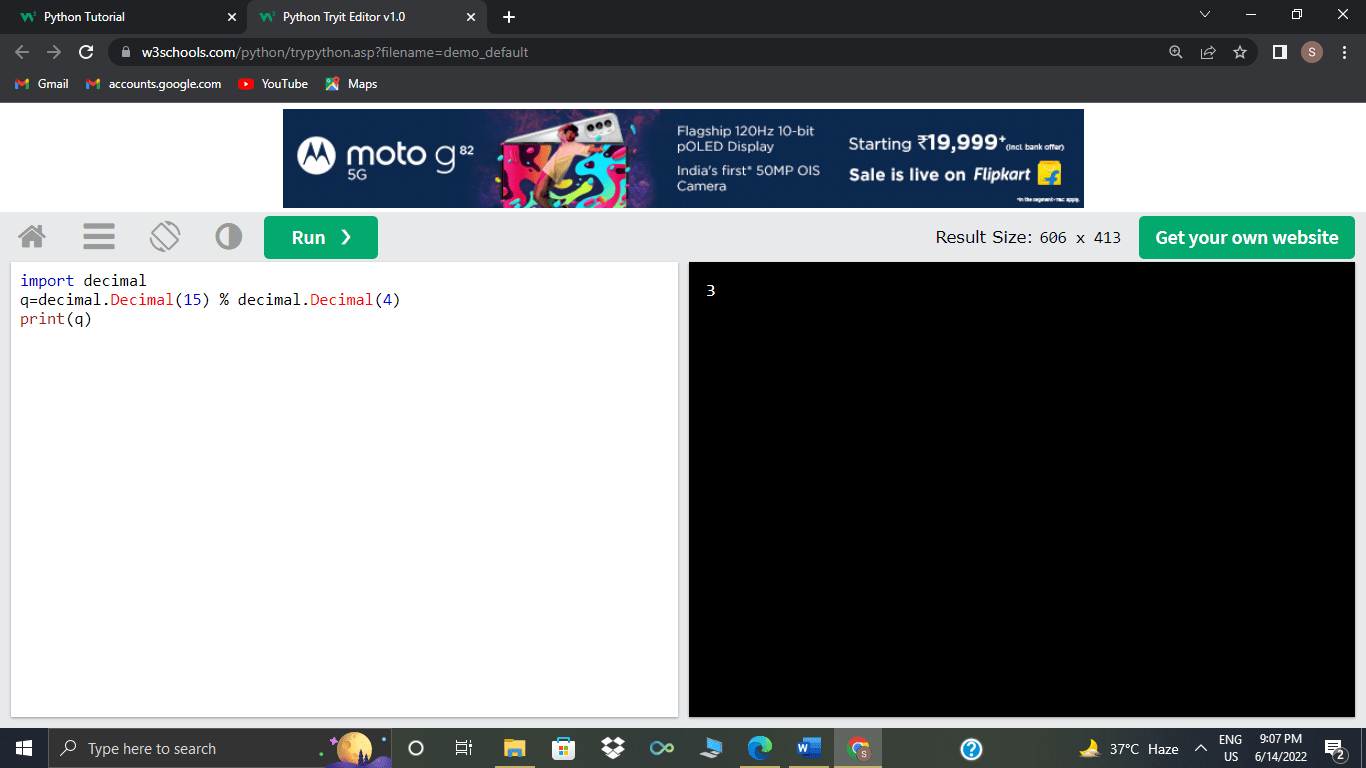
import decimal
Q=decimal.Decimal(15) % decimal.Decimal(4)
print(Q)
Now let’s look at some of the examples of using some floating-point numbers with decimal.Decimal and the modulo operator(%);
Example:
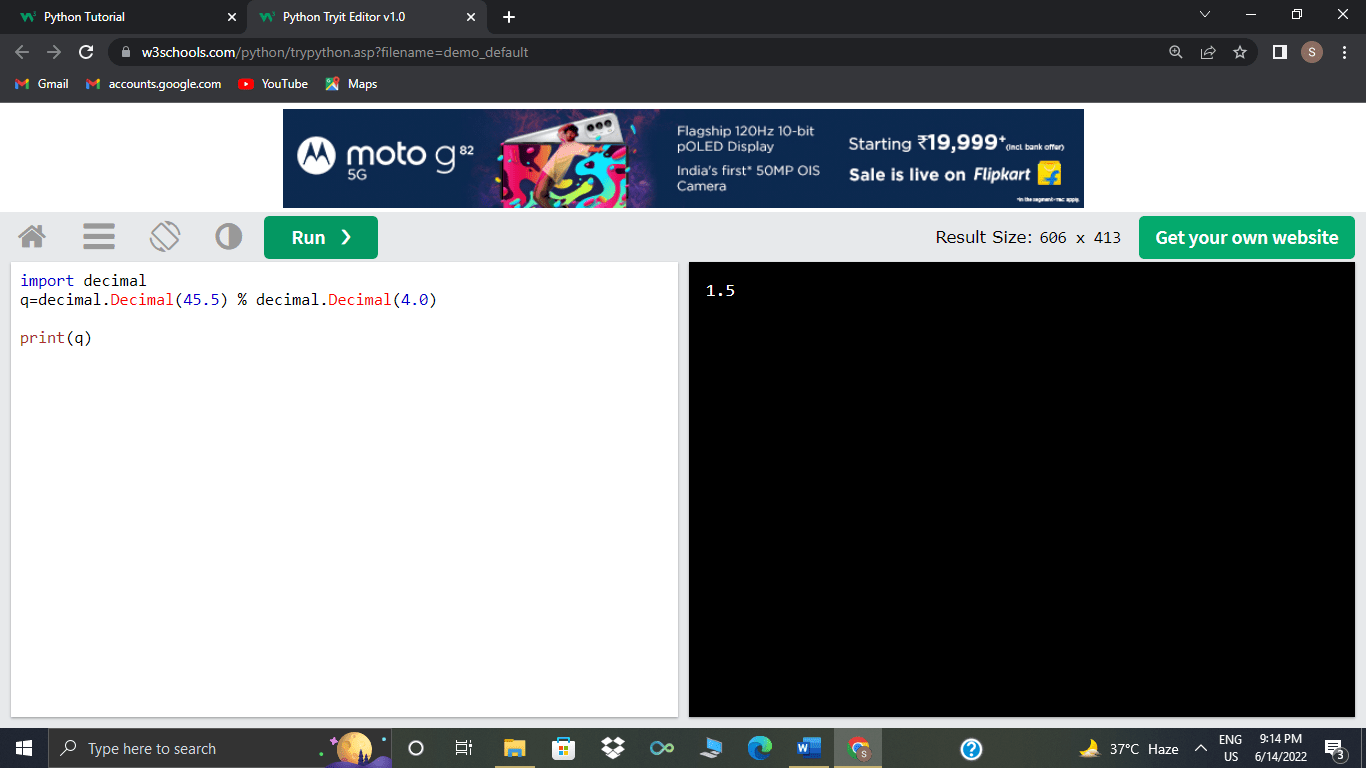
import decimal
decimal.Decimal(45.5) % decimal.Decimal(4.0)
Precedence
Like other Python operators, the modulo operator has precise rules that determine its precedence while evaluating expressions. The precedence of the Modulo operator in Python is the same as that of the operators given below.
Multiplicationà (*),
division à(/),
floor division à(//) operations.
Let’s look at an example of the modulo operator’s precedence given below:
>>>5 * 10 % 16 – 9
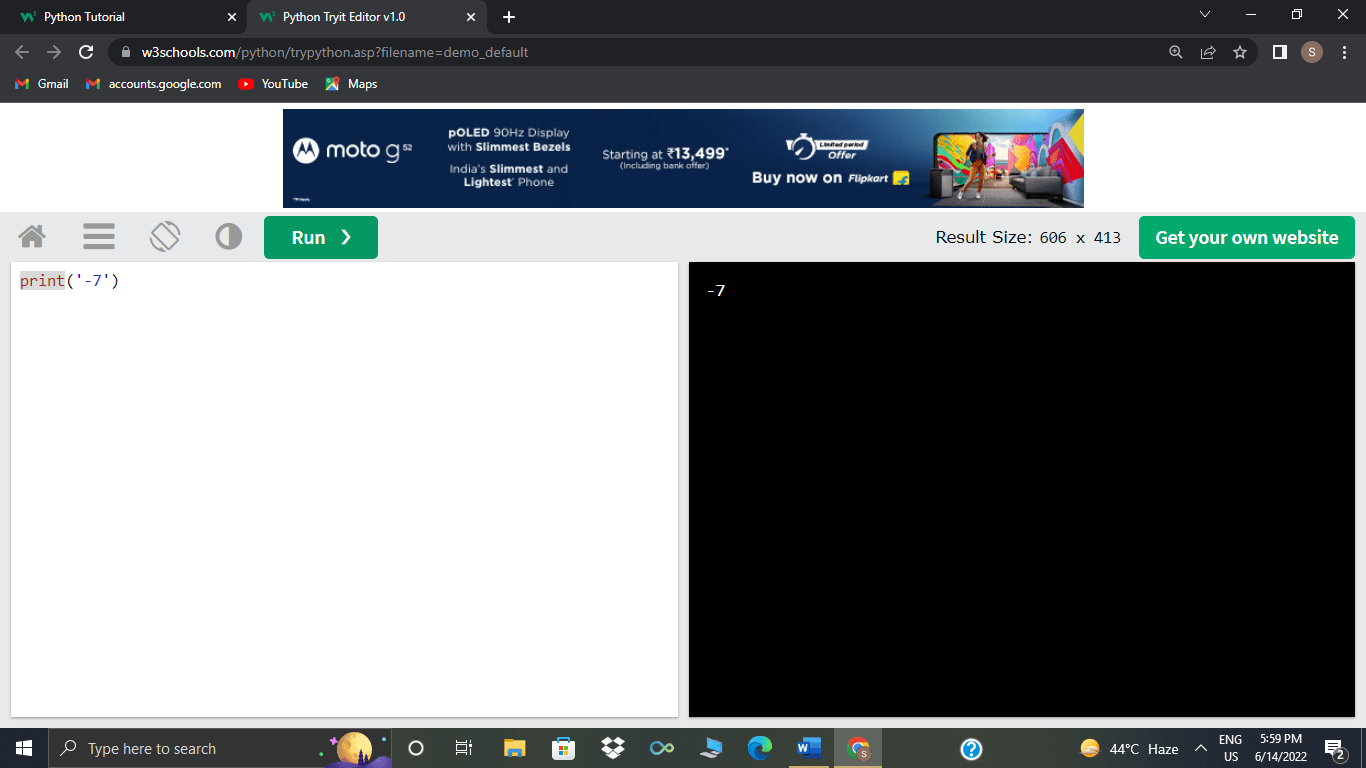
Since the level of precedence of multiplication and that of modulo operator is similar thus, with the associativity rule, Python will evaluate them from left to right. The following are the steps for the aforementioned operation;
Firstly,5 * 10 is evaluated, becoming 50 % 16 - 9.
- 50 % 16 is evaluated, becoming 2 - 9.
- 2 - 9 is evaluated, becoming -7.
Use parentheses to wrap the operation you want to be first evaluated before other operations if you want to override the precedence of other operators.
>>>5 * 10 % (16 - 9)
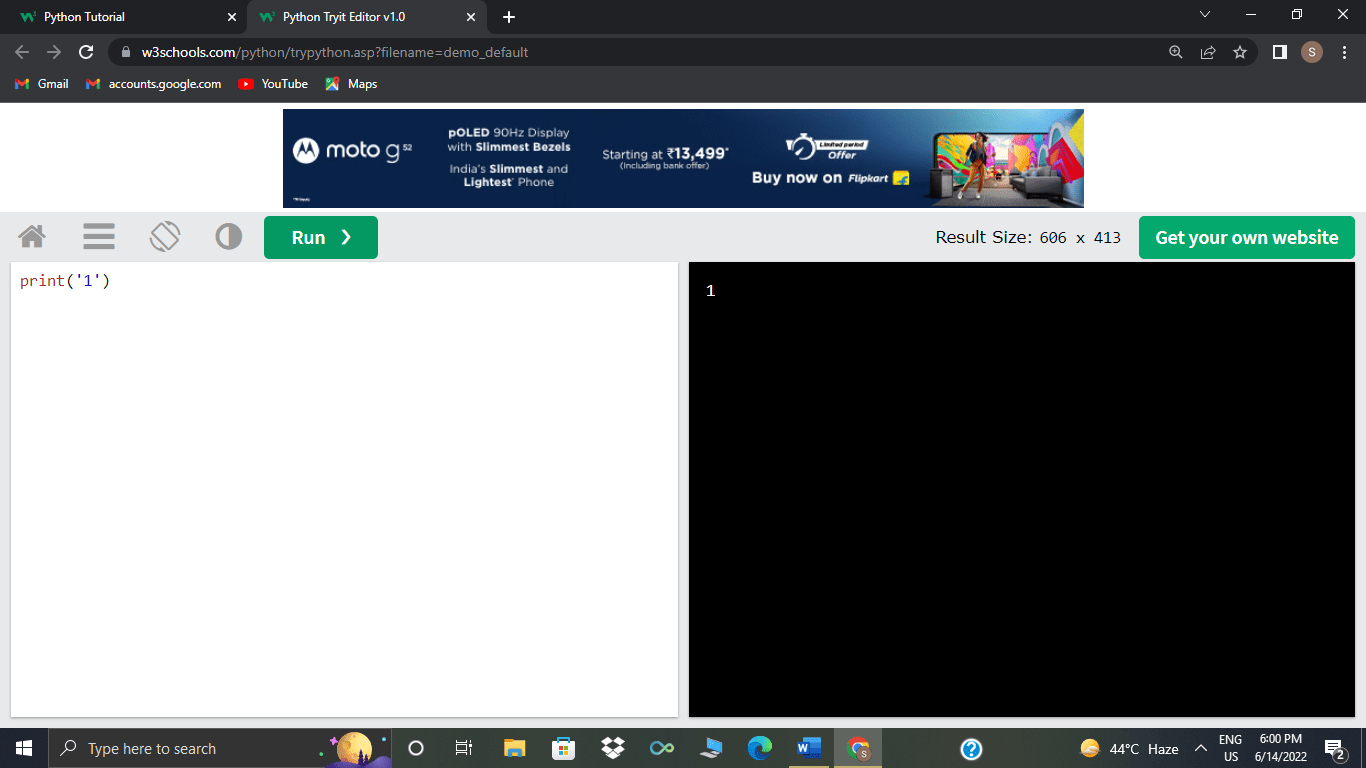
Here, in the example above, (16 - 9) is evaluated firstly, then 5 * 10 and at last 40 % 3, which equals 1.
Using Python Modulo Operator to solve Real-World Programming Problems;
Some examples are given below, which will give you all an idea of how Python Modulo Operator can be used.
- A Number is Even or Odd (Checking by Python Modulo Operator)
The modulo operator can check whether a given number is even or odd. Any number can be checked to see if it is evenly divisible by 2 by using the modulo operator with a modulus of 2. It's an even number if it's evenly divisible.
Here is a python program below checking whether the given number by the user is even or odd by using the modulo operator.
number=int(input(“enter a number:”))
if (number%2==0):
print(“Number is even”)
else:
print(“Number is odd”)
Here if the given number by the user is even, let's say 6, then 6%2 will yield 0, making the if condition true as a result, the statement inside if will be printed and if it’s odd, let's say 9, then 9%2 will yield 1 which is a non-zero number; therefore the statement inside else would be printed.
- Running the code at particular intervals in a Loop.
Running the Code in a Loop at Specific Intervals The Python modulo operator can be used to execute code at predetermined intervals inside of a loop. This is accomplished by performing a modulo operation on the loop's current index and a modulus. The modulus number defines how often the loop's interval-specific code runs.
- Creating cyclic iteration
The modulo operator can be used to produce cyclic iteration. Cyclic iteration is a sort of iteration that resets once it reaches a specific point. This sort of iteration is commonly used to restrict the iteration's index to a certain range.
- Converting units
Here we will see how to convert units with the modulo operator. The example below shows how to convert smaller units to larger ones without using decimals. The modulo operator finds any remainder when the smaller unit is not evenly divisible by, the larger unit.
Let’s convert inches to feet in this first example. The modulo operator is used to get the remaining inches that aren't evenly split into feet, and the floor division operator (//) is used to round down the total feet:
def inches_to_feet(given_inches):
inches = given_inches % 12
feet = given_inches // 12
print(f"{given_inches} inches = {feet} feet & {inches} inches")
Now let’s see an example of the function in use:
>>>inches_to_feet(350)
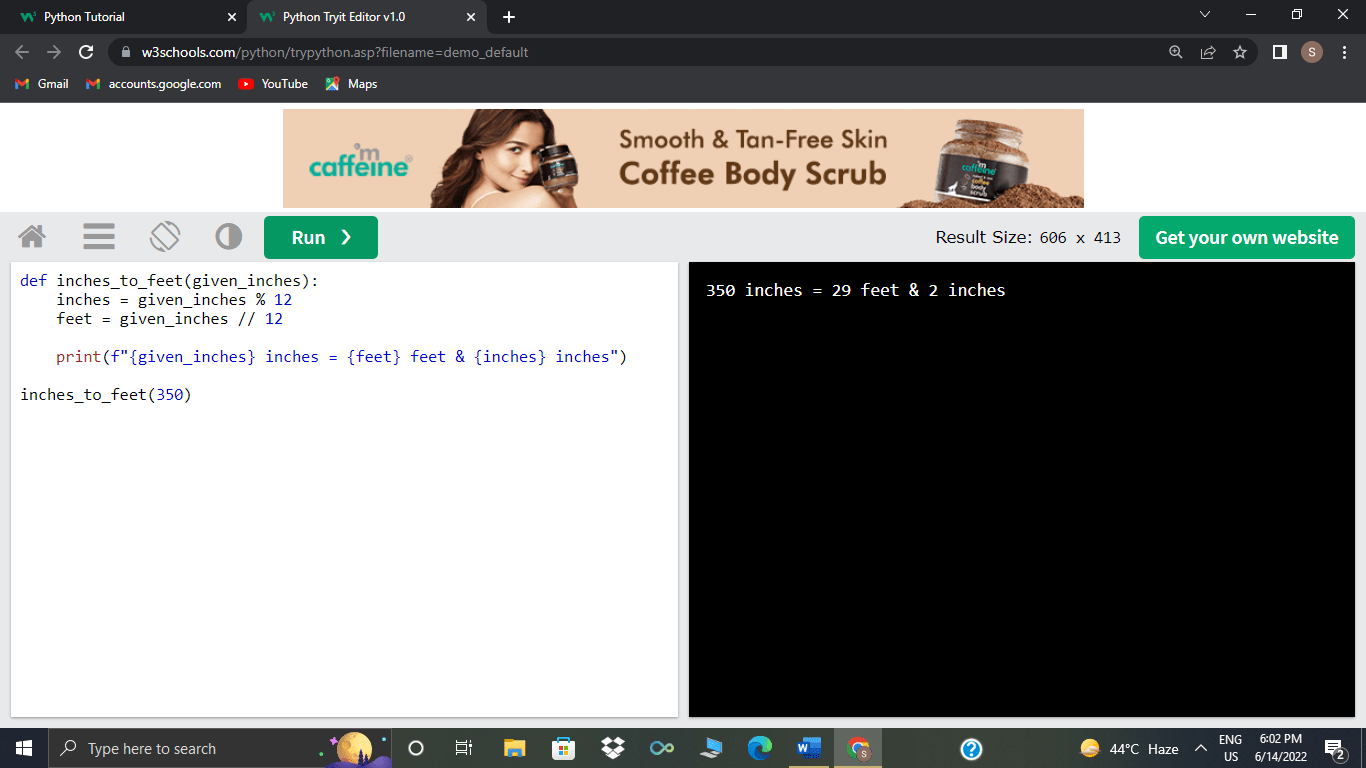
From the output, one can observe that 350%12 yields 2, which is the number of inches not evenly divided into feet. The total number of feet equally divided by the inches is 29, which results in 350/12.
- Determining if a Number Is a Prime Number
Now let’s see how to use the Python modulo operator to determine whether a number is prime. A prime number is a number that has only two elements: 1 and itself. 2, 3, 5, 7, 23, 29, 59, 83, and 97 are a few examples..
Code to check the primality of a number.
def prime_number_checking(number):
if number <2 :
print(f “(number) should be greater than or equal to 2 in order to be prime.”)
return
fac = [ (1, number)]
a=2
while a*a <= number:
if number % a ==0:
fac.append { (a, number//a))
a+=1
if len(fac) > 1:
print(f “Given number, (number) is not prime. It’s factors are as follows: (fac)” )
else:
print(f “Given number, (number ) is a prime number” )
Here is the output while passing different numbers.
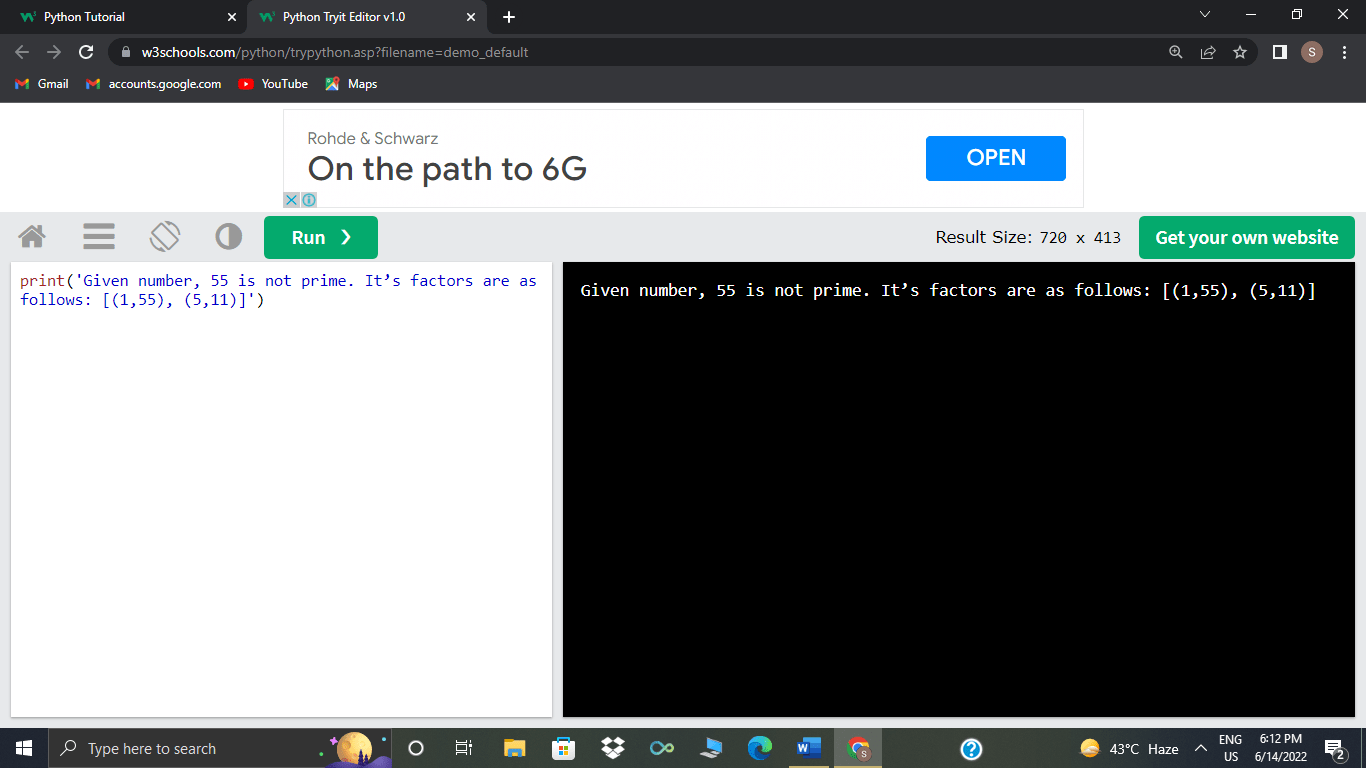
>>>prime_number_checking(55)
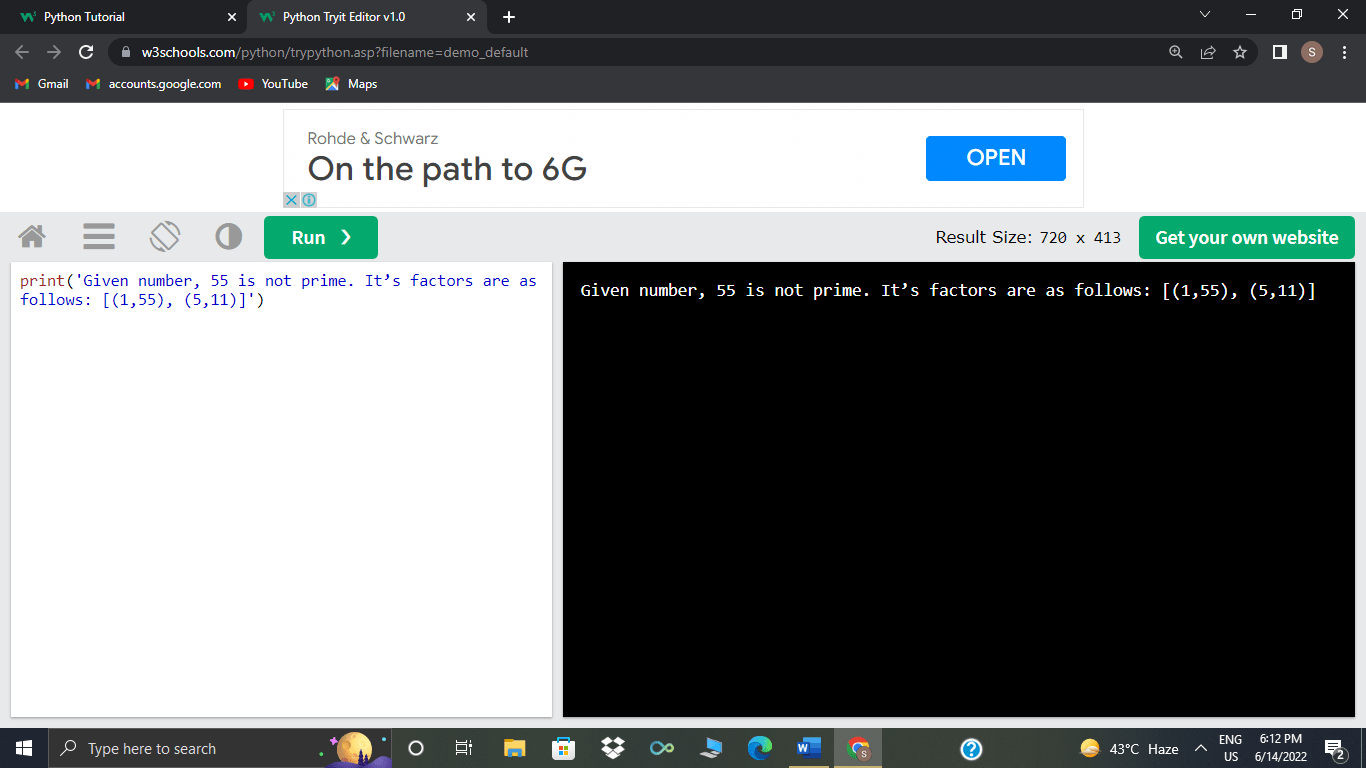
>>>prime_number_checking(13)
Conclusion
The Python modulo operator(%) is something to give your attention to surely. This operator can do much more than one can think, as seen above with its application in practice, like checking for even and odd numbers, Converting units, etc. This operator has so many usages, and it eases out our coding.