Python Permutations and Combinations
In mathematics, we all studied what is meant by permutations and combinations. “Permutations” define the way of arranging the elements in sequential order. “Combinations” mean the way of selecting the numbers from a given group of elements or collection of elements here; there is no particular order like permutations to follow. The main difference between these two is only "ordering", and the similarity is both are "mathematical concepts."
Often these are related to one another or swap each other without awareness.
For example, take a phone password. It may have combinations of alphabets and numbers and only alphabets and only numbers. It is mandatory to keep a password on our phones so that it should be in any of the above cases. For unlocking our phones, it is mandatory to enter the exact and correct combinations of alphabets, numbers, symbols, special characters, etc., in the correct order. It is known as “permutations” In the case of no order specification, we call it a "combination". It is a topic in probability and distributions.
To calculate permutation, we have a formula
nPr=(n!) / (n-r)!
where 'n' is the set of elements, and 'r' is an arrangement of those elements.
To calculate the combination, we have a formula
nCr = n! / r! * (n-r)!
where 'n' is the set of elements, and 'r' is the number of elements chosen at a time. Here we use an "inbuilt package" to find permutations and combinations for a given number. The "itertools library" in python has built-in functions to calculate permutations and combinations.
We can import the itertools library by using the below command.
import itertoolsThe above import statement provides the itertools library and imports with the itertools library, forming a path to their functions.
Permutations mean arranging the elements in order, and these elements can be a string, any data type, and a list. It means it is the arrangement of elements in different ways.
Suppose there are 'n' elements, and the number of permutations is calculated by "n!". That is if there are 3! = 3*2*1=6 permutations of {1,2,3} are {1,2,3}, {1,3,2}, {2,1,3}, {2,3,1}, {3,1,2}, {3,2,1}.
Python will do these mathematical functions with a library called itertools in a python interpreter.
Let us write a simple python program representing the concept of "permutations".
Example 1 by the normal method
#Python program to print all the permutations using the built-in library called itertools
from itertools import permutations
#Here, we get the permutations of the given elements
pm = permutations ([1,2,3])
#Printing the number of permutations
for i in list (pm):
print(i)
Output

The above output shows all the permutations of the given elements. It gives "n!" permutations if the input element sequence length is "n".
Let us take another example to get permutations of specific length "L".
Example 2
#Python program to print all the permutations using the built-in library called itertools
from itertools import permutations
#Here, we get the permutations of the given elements
pm = permutations (['1','2','3'])
#Printing the number of permutations
for i in list (pm):
print(i)
Output
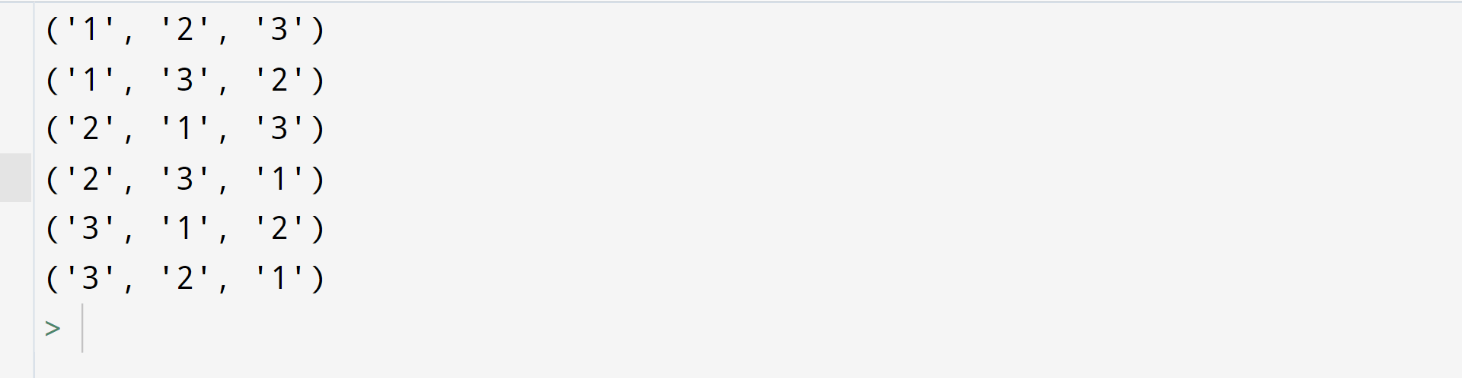
From the above example, we had given a single quote for every input, and the output was in the above format and looked efficient.
Example 3 by giving fixed length
#Python program to print all permutations of the length given
from itertools import permutations
#Here, we get all the permutations of length 2
pm = permutations ([1,2,3],2)
#Printing all the possible permutations
for i in list(pm):
print(i)
Output

The above output gives the number of possible permutations if the length is a specified parameter. From the mathematical calculation, it generates nCr * r! permutations. If the input sequence length is "n" and the given input parameter is "r".
What is Combinations?
As we discussed earlier, Combinations mean the way of selecting the numbers from a given group of elements or collection of elements here; there is no particular order like permutations to follow. It takes input as a "list" and also "r" as an input, and it will return a list of tuples that contain a total combination of inputs and length "r."
Let us take an example showing how combinations work with a given input.
Example
#Example python program to print the number of combinations of the given length
from itertools import combinations
#Take a length 2 with the combinations of [1,2,3]
cms = combinations ([1,2,3],2)
#Printing all the combinations required from the given input
for i in list(cms):
print(i)
Output

We noticed from the above output that the combinations are the combinations of the given input with a given length as an input.
There will be no repetition of elements in the combination's method, whereas, in permutations, there will be a repetition of elements.
Python Permutations and Combinations
Permutations are the number of possible arrangements in an ordered set of objects. Combinations are arrangements of objects without regard to order, select from several objects. If the order does not matter, it is a combination. If the order does matter, it is a permutation.
We discussed many examples, and now we discuss an example related to permutations by taking a parameter called "range".
We should import a library called itertools, which contains all the functions that need permutations and combinations.
Example Program for Permutations
import itertools
permut = itertools.permutations(range(1,4),3)
#permut = itertools.permutations([1,2,3],3)
count_permut = []
for i in permut:
count_permut.append(i)
#print all permutations
print(count_permut.index(i)+1,i)
#print total number of permutations
print("number of permutations", len(count_permut))
Output
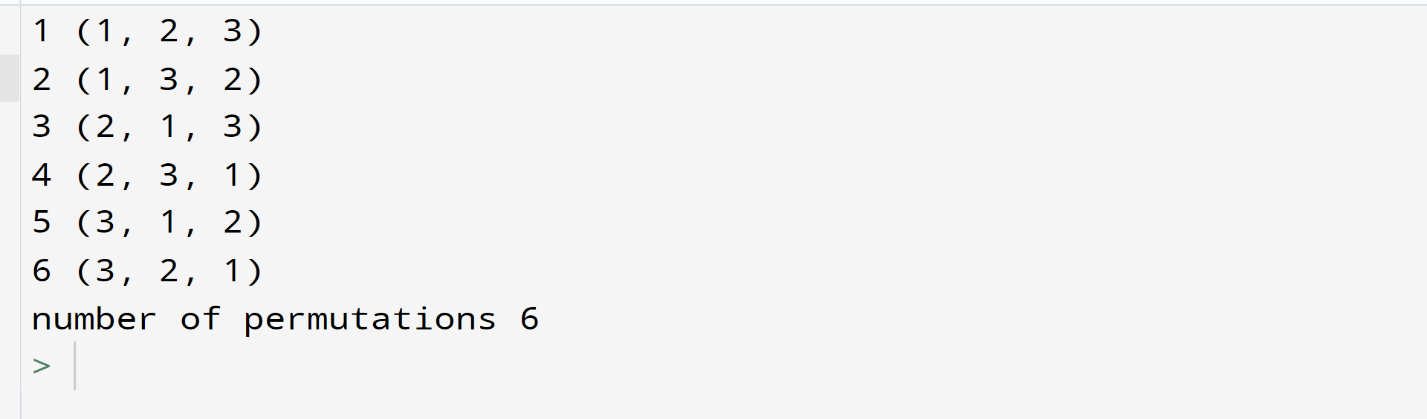
The first thing we did to find all permutations, we create a variable, then we assigned a variable named "permut", and then we assigned the itertools module. We used a dot to access the permutations' function, and then inside the brackets for the permutation's functions, we put the data that we want to find the permutations. So, in this case, the first argument we used is "range" to put our iterable, and this will be numbers from 1 to 7 but not including 7. So, it will be a range of 6 numbers, and from those 6 numbers, we want to find the permutations for links of 3 or sets of 3.
Definition: permutations(iterable(, r))
Type: Function of itertools module
Here the first argument is "iterable," which is our range of numbers, and the second argument, "r," is the length of the set. In this example, we had given a range of "three," and for the second argument, we had given "2". We saw in an output that the numbers that come out are in sets of "two".
Example program for Combinations
import itertools
combin = itertools.combinations(range(1,7),3)
#combin = itertools.combinations([1,2,3,4,5,6],3)--> we use this case when we do not want the "range parameter".
count_combin = []
for i in combin:
count_combin.append(i)
#print all combinations
print(count_combin.index(i)+1,i)
#print total number of combinations
print("number of combinations", len(count_combin))
Output
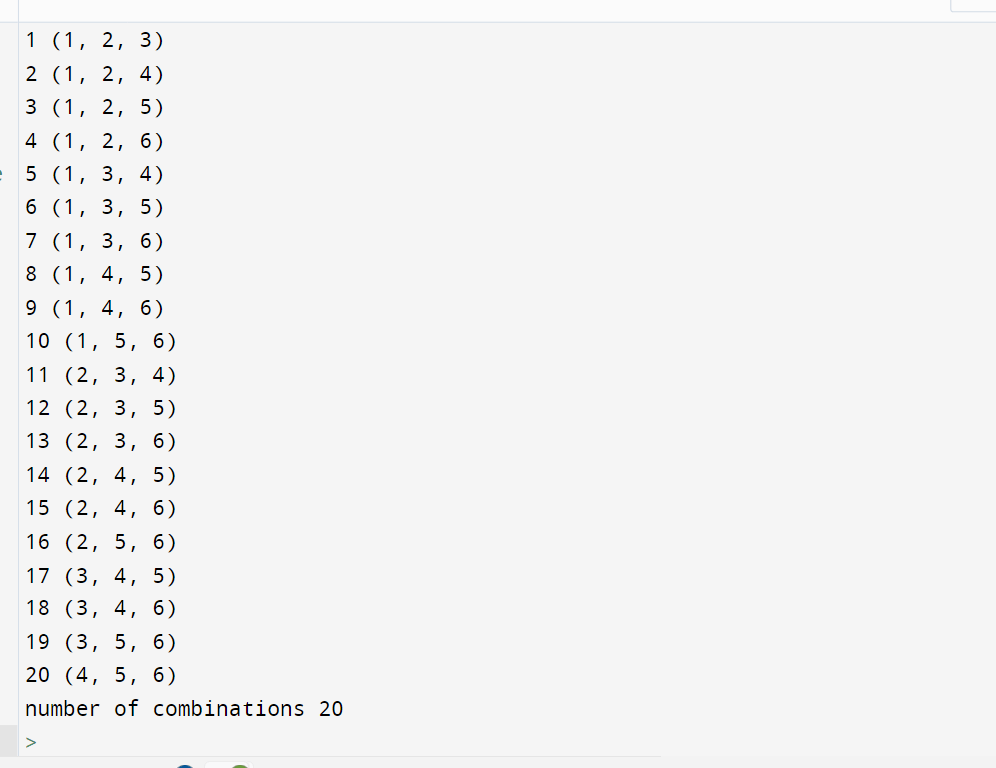
From the above output, we noticed many combinations of given inputs. No repetition is allowed because it is the concept of combinations, and it will give the arrangements without any use of order. Here we used a variable called "combin," The remaining program code is the same as permutations, but not the variable.
In permutations, arrangements will be repeated like an arrangement can be of the order and reverse of the order. But combinations won't allow these things.
Combinations Using String
The itertools module in python provides the permutations and combinations method to calculate the given data. Like that, we can also calculate the combination of a string. Let us take one example.
import itertools
string = "Python"
combin_string = itertools.combinations(string,2)
for s in combin_string:
print(s)
Output
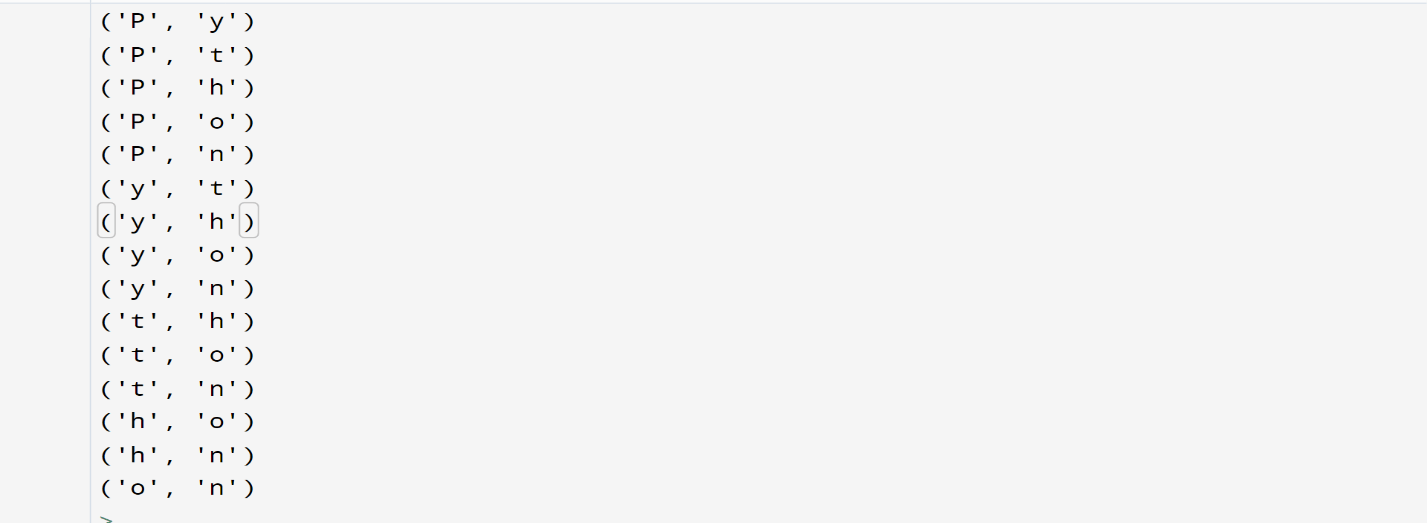
We observed that the output is formed by the combinations of the given string "Python." Any combination is not repeated from the above output.
A new concept for combinations based on replacement; is known as "Combination with Replacement." This concept is based on considering the string, number, or alphabet by taking self.
Example of Combination with Replacement
from itertools import combinations_with_replacement
cm = combinations_with_replacement(["Python"],2)
#print all the combinations along with replacement
for s in list(cm):
print(s)
Output

From the above example, we observed that we had given a string named "Python," and the length of the string was "2." So the output produced was the "python" followed by "python. The replacement concept will repeat string, alphabet, or numeric repetition by considering itself.
Another Example Showing the concept of combinations_with_replacement
from itertools import combinations_with_replacement
cm = combinations_with_replacement(['P','y','t','h','o','n'],2)
#print all the combinations along with replacement
for s in list(cm):
print(s)
Output
Here we observed a combination of alphabets with one another, replacing alphabets like 'p' 'p' and 'y' 'y', etc.
Another method for combinations with a replacement is the combination of a set of numeric types of data.
It explains that if we give input well-mannered, the output produced will be tuples with sorted and well-mannered.
Example Program
import itertools
n = [4,5,6,7]
cm_order = itertools.combinations_with_replacement(n,3)
for i in cm_order:
print(i)
Output

From the output, we observed the repetition of numbers in sorted order. If one number combination is completed, then another number combination will take place with replacement and repetition.
Applications of Permutations and Combinations
- Arrangement of seats in an exam hall or any occasion.
- We can use permutations and combinations for solving, creating, and breaking code. It involves guessing strings, alphabets, or numbers in the correct order.
- We can find the mobile numbers available on our phones using this concept.
- In technical, permutations provide a sequence of numbers, strings, or alphabets that should be unique from the given inputs. In contrast, combinations are only an arrangement of numbers, strings, and alphabets rather than sequencing.
Conclusion
Permutations in python play an important role in providing a concept of sequencing or ordering given numbers, characters, etc. Combinations provide the concept of the arrangement of elements without order.