Python Program for Linear Search

Introduction

We employ specific algorithms to efficiently carry out our responsibilities, such as searching for an element in a given data structure. These algorithms fall under the category of searching algorithms. Searching algorithms include the following: the interpolation search algorithm, the linear search algorithm, the jump search algorithm, the binary search algorithm, etc.

The earliest and most basic searching algorithm out of all of these is the linear search method. This post will teach us how to build the Linear Search Method on a data structure and will also look at the Python3 implementation of the algorithm.

What is the Linear Search?

• Finding items within a list can be done using a linear search strategy. Another name for it is a sequential search. Because it sequentially finds the required element, it is the easiest searching algorithm.
• Every element is compared to the value that we are looking for. The element is found as well as the algorithm returns its key’s index position if both match.
• The elements of a linear search don't have to be put in sorted order.
• It is founded on a sequential technique.
• Any linear data structure, including a linked list, array, etc., can be used to implement the linear search.
• Both a single-dimensional array and a multidimensional array can use it.
• The worst-case scenario for locating the element in the linear search is O (n).
• The best-case scenario for discovering the first entry in a list in a linear search is O (1).
• In the event of huge data sets, it is less effective.

Procedure:

When learning DSA (data structures and algorithms) for the first time, beginners frequently start with the linear search method. Let's use an illustration to demonstrate how the linear search algorithm can be used.

Let's say we want to look for the value=30 in the following data, which is in a Python List.

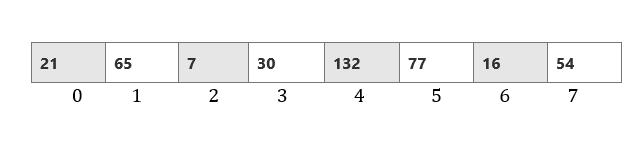
• Step 1: We take into account the first value, which is 21 from the list, and compare it to our search value, which is 30. We go on to the following value in the list because it is not equal.

• Step 2: Next, we take into account the second factor, 65, and contrast it with the value of 30. We proceed to the following element once more because it is not equal.

• Step 3: Our list now includes seven items. When we compare the two components, we discover that 7 is not equivalent to 30. We now go on to the next component.

• Step 4: Element 30 is now on our list. 30 is compared to value = 30. We have located the element we were looking for in the list since 30 is equivalent to 30. The element's index value = 3 can then be returned for use in subsequent calculations after we print a message indicating that the element has been located.

This is an iterative process, as you can see, so this iteration will keep going until the preferred value is found or it moves to the end of the list. When it reaches the end of the list but no such element is there, it can display the message informing the user that such an element is not present.

This is the linear search algorithm, which you must have found to be fairly easy.

The complexity of Time:

1. O(n), where n is the total number of elements in a list, is the worst case. The loop must be run n times in the worst-case scenario where the element is at the end of the list.
2. Optimal Case: O (1). In the ideal scenario, the element appears at the top of the list.
3. Case-average O (n). O(n) time complexity is obtained by adding up the total amount of time spent on each entry in the list and calculating their average.

Implementation of Python 3

Let's now see how this technique can be implemented in Python.

Code:

def linear_search (list_1, value):
    for i in range (len (list_1)):
        if list_1[i]== value:
            return i
    return -1


list_1=[21, 65, 7, 30, 132, 77, 16, 54]
x= int (input (" Enter the value you want to search in the list\n"))




index = linear_search (list_1, x)


if index == -1:
    print ("Search Complete! The element do not present in the list!")
else:
     print ("Search Complete! The element found at index " + str(index))

Now that we have the input of 30, let's examine the result:

Enter the value you want to search in the list
30
Search Complete! The element found at index 3

Let's look at what happens if we enter a number that isn't on the list, like value = 980:

Enter the value you want to search in the list
980
Search Complete! The element does not present in the list!

Because there are no 980 elements in the list, that is in fact the right outcome.

Conclusion

In this post, we have examined what a linear search algorithm is as well as in-depth examples of how to use it to find a certain element in a list. Finally, we demonstrated how we might use Python 3 as a language to actually execute the Linear Search Algorithm and obtain the results we needed.

Some Most Popular Questions

1. What are the linear search's space and time complexity?

When the data isn't ordered, linear search is a good strategy, however, it can be time-consuming. The program's memory usage and how long the compiler needs to run the program determine the time and space complexity, respectively. The time and space complexity of the linear search is listed below.

2. What is Interpolation Search?

The optimized variant of binary search, interpolation search, find the key element on average in O(log(log n)) time. In binary search, the mid of the array is the first place we always look. But using this approach, the search could lead to various places based on where the key is. The search will begin at the end of the array, for example, if the key is close to the final element.