Python Program for Tower of Hanoi
In this tutorial, we will examine and learn about the Python coding used to create the video game Tower of Hanoi. Before seeing the game's step-by-step implementation in Python, we will first learn about the game's rules. Without spending any time, let's begin.
In python, what is the Tower of Hanoi?
Three identical rods and n discs of various sizes are used in this mathematical puzzle game. The discs are arranged in the first rod with the largest disc at the bottom and the smallest disc at the top.The disc must be placed in the final rod via the intermediate rod in the same order in order to complete the puzzle.
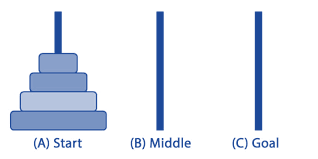
Rules of Tower of Hanoi in Python:
- One disc can only be moved at a time.
- Only the top disc could be moved and positioned on top of any other rod.
- Only larger discs can be stacked on top of smaller ones.
An example of the game:
Consider that there are initially 3 discs set up as follows.
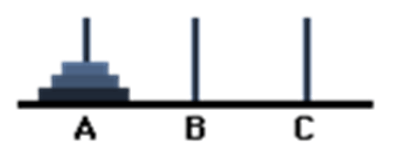
Move- 0
We'll initially transfer the disc from A to C.
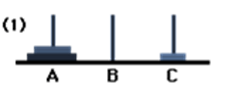
Move: 1
Moving the disc now from A to B
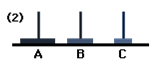
Move: 2
The disc of rod C will then be moved to position B.
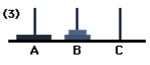
Move: 3
Following this, the disc will be transferred from A to C.
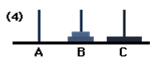
Move: 4
Transfer the disc now from B to A.
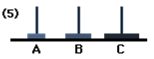
Move: 5
The disc of rod B must then be moved to rod C.
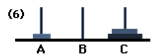
Move: 6
Finally, we will transfer the disc from position A to position C to complete the puzzle.
Move: 7
Tower of Hanoi implementation in Python:
Code:
def tower__of__hanoi(number, start, aux, end):
if (number == 1):
print ('Moved disk 1 from rod {} to rod {}'.format (start, end))
return
tower__of__hanoi(number - 1, start, end, aux)
print ('Moved disk {} from rod {} to rod {}'.format (number, start, end))
tower__of__hanoi(number - 1, aux, start, end)
number = 3
tower__of__hanoi (number, 'A', 'B', 'C')
Output:
Moved disk 1 from rod A to rod C
Moved disk 2 from rod A to rod B
Moved disk 1 from rod C to rod B
Moved disk 3 from rod A to rod C
Moved disk 1 from rod B to rod A
Moved disk 2 from rod B to rod C
Moved disk 1 from rod A to rod CExplanation:
Here, the game's implementation was done using a recursive approach.
- The TowerOfHanoi() function requires four inputs.
- Quantity of discs
- source rod
- supporting rod
- target rod
- If the number of discs is 1, this first checks the condition, pushes the disc immediately to the destination rod, and then ends the function.
- The rest n-1 discs were then recursively moved from the source node to the supporting node utilizing the target rod as the auxiliary node.
- The final disc is then immediately transferred from the source rod to the supporting rod.
- Finally, using the source node, we have once more run the function recursively to transfer the rest n-1 rods from the supporting rod to the target rod.
Can the Tower of Hanoi be solved without recursion?
It's possible for anyone to have this thought. Yes, it is undoubtedly feasible. By using a binary solution strategy, where the n number of discs are encoded and represented as the numbers 0 - 2n, the tower of Hanoi problem can also be solved non-recursively.
The recursive solution's time complexity:
Tower of Hanoi's recursive solution has an O(2n) time complexity, wherein n is the number of discs.
Conclusion
In this article, we gained in-depth information about the Tower of Hanoi game and its Python recursive implementation. Along with thoroughly developing the game's concept, we also discovered a simple Python implementation.