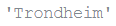Python 2.7 data structures

The rundown information type has a few additional techniques. Here is every one of the strategies for listing objects:

list.append(x): Add a thing to the furthest limit of the rundown; comparable to a[len(a):] = [x].

list.extend(L): Broaden the rundown by annexing every one of the things in the given rundown, identical to a[len(a):] = L.

list.insert(i, x): Embed a thing at a given position. The main contention is the record of the component before which to embed, so a.insert(0, x) embeds at the front of the rundown, and a.insert(len(a), x) is comparable to a.append(x).

list.remove(x): Eliminate the principal thing from the rundown whose worth is x. It is a blunder assuming there is no such thing.

list.pop([i]): Eliminate the thing in the given situation in the rundown, and bring it back. Assuming that no record is determined, a.pop() eliminates and returns the last thing in the rundown. (The square sections around the I in the technique signature mean that the boundary is discretionary, not that you ought to type square sections at that position. You will see this documentation often in the Python Library Reference.)

list.index(x): Return the record in the rundown of the primary thing whose worth is x. It is a blunder assuming that there is no such thing.

list.count(x): Return the times x shows up in the rundown.

list.sort(): Sort the things of the rundown, and set up.

list.reverse(): Turn around the components of the rundown, and set up.A model that utilizes the greater part of the rundown strategies:

Example

a = [66.25, 333, 333, 1, 1234.5]
print(a.count(333), a.count(66.25), a.count('x'))

Output:

Using Lists as Stacks

The rundown techniques make it extremely simple to involve a rundown as a stack, where the last component added is the primary component recovered ("rearward in, first-out"). To add a thing to the highest point of the stack, use attach(). To recover a thing from the highest point of the stack, utilize pop() without an unequivocal file.

For instance

stack = [3, 4, 5]
stack.append(6)
stack.append(7)
stack

Output

Using Lists as Queues

It is likewise conceivable to involve a rundown as a line, where the principal component added is the main component recovered ("first in, first out"); be that as it may, records are not proficient for this reason. While adds and pops from the finish of rundown are quick, doing supplements or pops from the start of a rundown is slow (on the grounds that different components must be all moved by one).

To carry out a line, use collections.deque, which was intended to have quick annexes and pops from the two closures. For instance:

from collections import deque
queue = deque(["Eric", "John", "Michael"])
queue.append("Terry")           # Terry arrives
queue.append("Graham")          # Graham arrives
queue.popleft()  

Output:

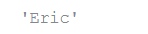
Another example

queue.popleft()           
queue

Output:

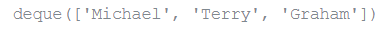
Functional Programming Tools

There are three inherent capabilities that are extremely valuable when utilized with records: channel(), map(), and diminish().

filter(function, sequence) returns a grouping comprising of those things from the succession for which function(item) is valid. On the off chance that succession is a string or tuple, the outcome will be of a similar kind; in any case, it is generally a rundown. For instance, to register a few primes:

def f(x): return x % 2 != 0 and x % 3 != 0
filter(f, range(2, 25))

Output:

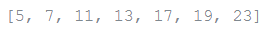
Map(function, sequence) calls a function(item) for every one of the succession's things and returns a rundown of the brought values back. For instance, to register a few solid shapes:

def cube(x): 
	return x*x*x
map(cube, range(1, 11))

Output:

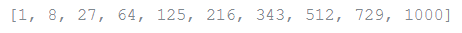
More than one grouping might be passed; the capability should then have however many contentions as there are arrangements and is called with the relating thing from each succession (or None in the event that some grouping is more limited than another). For instance:

seq = range(8)
def add(x, y): 
	return x+y
map(add, seq, seq)

Output:

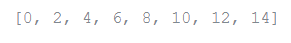
On the off chance that there's just a single thing in the succession, its worth is returned; assuming the grouping is unfilled, a special case is raised.

A third contention can be passed to demonstrate the beginning worth. For this situation, the beginning worth is returned for an unfilled succession, and the capability is first applied to the beginning worth and the primary arrangement thing, then to the outcome and the following thing, etc. For instance,

def sum(seq):
def add(x,y): 
	return x+y
return reduce(add, seq, 0)

Output:

List Comprehensions:

List understandings give a compact method for making records without falling back on utilization of guide(), channel() or potentially lambda. The subsequent rundown definition frequently tends to be clearer than records fabricated utilizing those builds. Each rundown cognizance comprises of an articulation followed by a for provision, then at least zero for or on the other hand if statements. The outcome will be a rundown coming about because of assessing the articulation with regards to the for and on the off chance that provisions which follow it. In the event that the articulation would assess to a tuple, it should be parenthesized.

freshfruit = [' banana', ' loganberry ', 'passion fruit']
[weapon.strip() for weapon in freshfruit]

Output:

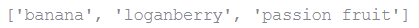
vec = [2, 4, 6]
[3*x for x in vec]

Output:

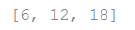
vec1 = [2, 4, 6]
vec2 = [4, 3, -9]
[x*y for x in vec1 for y in vec2]

Output:

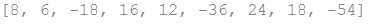
Nested List Comprehensions

Assuming you have the stomach for it, list appreciations can be settled. They are an incredible asset; however - like every amazing asset - they should be utilized cautiously, if by any means.

Consider the accompanying illustration of a 3x3 framework held as a rundown containing three records, one rundown for every column:

mat = [
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 9],
       ]

Presently, to trade lines and segments, you could utilize a rundown understanding:

print [[row[i] for line in mat] for I in [0, 1, 2]]

Output:

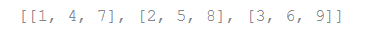
A more verbose rendition of this piece shows the stream expressly:

for i in [0, 1, 2]:
    for row in mat:
        print row[i],
    print

In a genuine world, you ought to favor working in capabilities to complex stream explanations. The zip() capability would work really hard for this utilization case:

zip(*mat)

Output

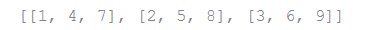
The del statement

There is a method for eliminating a thing from a rundown given its list rather than its worth: the del proclamation. This contrasts from the pop() strategy, which returns a worth. The del explanation can likewise be utilized to eliminate cuts from a rundown or clear the whole rundown (which we did prior to the task of an unfilled rundown to the cut). For instance:

a = [-1, 1, 66.25, 333, 333, 1234.5]
del a[0]
a

Output:

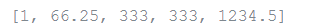
Tuples and Sequences

We saw that rundowns and strings have numerous normal properties, like ordering and cutting activities. They are two instances of arrangement information types (see Sequence Types — str, unicode, list, tuple, support, xrange). Since Python is an advancing language, other succession information types might be added. There is additionally another standard succession information type: the tuple.

A tuple comprises various qualities isolated by commas, for example:

t = 12345, 54321, 'hello!'
t[0]

Output:

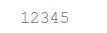
# Tuples may be nested:
u = t, (1, 2, 3, 4, 5)
u

Output:

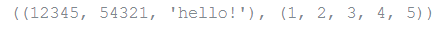
As you see, on yield tuples are constantly encased in brackets so that settled tuples are deciphered accurately; they might be input despite everything encompassing enclosures, albeit frequently brackets are important in any case (if the tuple is essential for a bigger articulation).

Tuples have many purposes. For instance: (x, y) coordinate matches, representative records from a data set, and so on. However, tuples, similar to strings, are changeless: it is beyond the realm of possibilities to expect to dole out to the singular things of a tuple (you can mimic a large part of a similar impact with cutting and connection). It is additionally conceivable to make tuples which contain changeable articles, like records.

An exceptional issue is the development of tuples containing 0 or 1 things: the sentence structure has a few additional idiosyncrasies to oblige these. Void tuples are developed by vacant sets of brackets; a tuple with one thing is built by following a worth with a comma (encasing a solitary worth in parentheses isn't adequate). Monstrous, yet compelling. For instance:

empty = ()
singleton = 'hello', # <- - note following comma
len(empty)

Output:

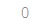
Sets

Python likewise incorporates an information type for sets. A set is an unordered assortment with no copy components. Fundamental purposes incorporate enrollment testing and taking out copy sections. Set protests additionally support numerical tasks like association, crossing point, contrast, and symmetric distinction.

Here is a short exhibit:

basket = ['apple', 'orange', 'apple', 'pear', 'orange', 'banana']
fruit = set(basket) # make a set without copies
fruit

Output:

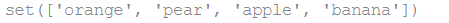
Dictionaries

One more helpful information type incorporated into Python is the word reference (see Mapping Types — dict). Word references are now and then tracked down in different dialects as "affiliated recollections" or "acquainted exhibits". Not at all like groupings, which are ordered by a scope of numbers, word references are filed by keys, which can be any changeless kind; strings and numbers can constantly be keys. Tuples can be utilized as keys in the event that they contain just strings, numbers, or tuples; if a tuple contains any impermanent article either straightforwardly or in a roundabout way, it can't be utilized as a key. You can't involve records as keys since records can be changed

And set up utilizing file tasks, cut tasks, or techniques like attach() and broaden().

It is ideal to consider a word reference an unordered arrangement of keys: esteem matches with the necessity that the keys are interesting (inside one-word reference). A couple of supports make a vacant word reference: {}. Putting a comma-isolated rundown of key: value matches inside the supports adds beginning key: value matches to the word reference; this is likewise how word references are composed on yield.

The fundamental procedure on a word reference is putting away a worth with some key and extricating the worth given the key. It is likewise conceivable to erase a key: value pair with del. Assuming you store involving a key that is as of now being used, the old worth related to that key is neglected. It is a blunder to separate a worth utilizing a non-existent key.

The keys() strategy for a word reference object returns a rundown of all the keys utilized in the word reference in an erratic request (on the off chance that you need it arranged, simply apply the sort() technique to the rundown of keys). To check whether a solitary key is in the word reference, utilize the in-watchword.

Here is a little model utilizing a word reference:

tel = {'jack': 4098, 'sape': 4139}
tel['guido'] = 4127
tel

Output:

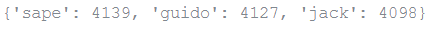
When the keys are simple strings, it is sometimes easier to specify pairs using keyword arguments:

dict(sape=4139, guido=4127, jack=4098)

Output:

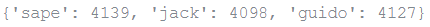
Looping Techniques

When looping through dictionaries, the key and corresponding value can be retrieved at the same time using the iteritems() method.

knights = {'gallahad': 'the pure', 'robin': 'the brave'}
for k, v in knights.iteritems():
	  print k, v

Outputs:

To loop over a sequence in sorted order, use the sorted() function which returns a new sorted list while leaving the source unaltered.

basket = ['apple', 'orange', 'apple', 'pear', 'orange', 'banana']
for f in sorted(set(basket)):
     print f

Output:

More on Conditions

The circumstances utilized in while and in the event that assertions can contain any administrators, not simply examinations.

The correlation administrators in and not in line whether a worth happens (doesn't happen) in a grouping. The administrators endlessly don’t look at whether two articles are actually similar items; this main matters for impermanent items like records. All examination administrators have a similar need, which is lower than that of every mathematical administrator.

Examinations can be tied. For instance, a < b == c tests whether an is not as much as b, and besides, b rises to c.

Examinations might be consolidated utilizing the Boolean administrators and or potentially, and the result of a correlation (or of some other Boolean articulation) might be refuted with not. These have lower needs than examination administrators; between them, not have the most elevated need as well as the least, with the goal that An and not B or C is identical to (An and (not B)) or C. As usual, brackets can be utilized to communicate the ideal synthesis.

The Boolean administrators and additionally are supposed short out administrators: their contentions are assessed from left to right, and assessment stops when they are not entirely settled. For instance, in the event that An and C are valid, however, B is misleading, and An and B and C doesn't assess the articulation of C. At this point, when utilized as a general worth and not as a Boolean, the return worth of a short-out administrator is the last assessed contention.

Doling out the consequence of a correlation or other Boolean articulation to a variable is conceivable. For instance,

string1, string2, string3 = '', 'Trondheim', 'Hammer Dance'
non_null = string1 or string2 or string3
non_null

Output: