Python SymPy
A Python package for symbolic mathematics is called SymPy. Its goal is to develop into a fully-fledged computer algebra system (CAS) while maintaining the code as straightforward as possible to make it understandable and simple to extend. All of SymPy's code is written in Python. The open-source Python package SymPy is used for symbolic computation. It offers computer program functions as a program, a library for other programs, or Property, accordingly, Live or SymPy Gamma. SymPy has few dependencies and is entirely written in Python, making it easy to install and inspect. SymPy is a special computer system with a reasonably low entry barrier due to its accessibility and a simple and extendable source code in a well-known language.
SymPy is written completely in python language and is a better extension of the python language to create symbolic mathematics. This SymPy uses an interactive tool embedded in other applications and extended with its random functions. Unit test reference values and various types of code creation are produced using Sympy. Quantum 1D Simple Harmonic Oscillator with Quantum Mapping Gate for Python Quantum Programming. SymPy is a component of the open-source mathematics program SageMath. For those with Python experience or those looking to incorporate mathematical intelligence into a Python project, SymPy is a good option.
Mathematical object calculations using symbols are the focus of symbolic computing. This suggests that mathematical equations with undetermined factors are left in symbolic form and that entities are presented accurately rather than crudely. And finally, Python is used to create SymPy. Most computer algebra systems design their language. With SymPy, not so. Python is used only for the development and execution of SymPy. This suggests that learning SymPy is much simpler since you already know Python because you are already familiar with the syntax (and if you can't understand, Python is quite easy to learn). Python is a well-established, tried-and-true language. While the SymPy creators are confident in their ability to create mathematical software, creating a programming language is a different challenge. Using an existing language, we can focus on the crucial components of mathematics.
Another system for computer algebra is called Sage, which uses Py as its computer language. Sage, on the other side, is large and takes more than a gigabyte to download. The advantage of SymPy's small weight is that. In addition to being small, it also has no requirements to save Python, making it nearly universal. Additionally, Sage and SymPy have different objectives.
Sage aims to be an all-inclusive math system with all the major open-source math systems connected to a single package. One of the accessible packages Sage offers is used when you utilize a function like integrate. Sage does indeed contain SymPy. On the other side, SymPy aims to be an ego system with every feature implemented within the platform. The ability to utilize SymPy as a library is a crucial feature. Although many, especially computer systems, are built to be interactive, it cannot be easy to automate or extend them. SymPy can be easily imported into your Python program or used in an active Python environment. Furthermore, SymPy has APIs that make it easy to include your unique functions.
Features:
Substitution: One of the most common operations using a mathematical equation is substitution. Every occurrence of it in a phrase has its meaning altered by substitution. To do this, the subs technique is employed.
Converting Strings to SymPy Expressions: It is possible to translate strings into SymPy statements using the simple function.
Lambdify: Subs and evolve are helpful for straightforward assessments, but there are more effective methods for evaluating an expression at many points. For instance, SymPy would be far slower than necessary if you evaluated an expression a thousand times, especially if machine precision is your only concern. Utilize the Pandas and SciPy packages instead. The simplest method for converting a SymPy statement into a numerically evaluable expression is to use the modify function.
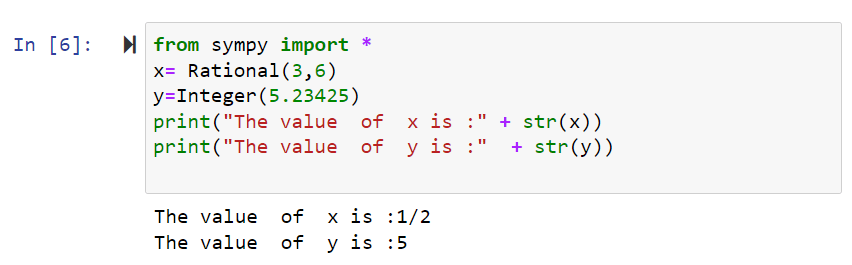
Simple calculator program using SymPy:
from sympy import *
x= Rational(3,6)
y=Integer(5.23425)
print(“The value of x is :” + str(x))
print(“The value of y is :” + str(y))
OUTPUT: