Cube Root in Python

In general, the cube is a three-dimensional solid figure that has 6 square faces. It is also called a geometrical shape with six equal faces, eight vertices, and twelve edges. A cube is also referred to as a regular hexahedron or a square prism. It is a type of 5 platonic solids.

There are some real-life examples of cubes, such as: an ice cube, a Rubik's cube, a regular dice, etc. The cube's length, breadth and height have the same measurement.

In mathematics or geometry, the cube is defined as a number that is multiplied itself by three times.

For example, the cube of 2 is 8, that is, 2*2*2. In Greek, the word cube is called "kybos", a six-sided die used in games. The cube in verb form is cut into cube shapes.

In algebra and arithmetic, the cube of a number "n" is its third power, multiplying three instances of "n" together. The representation of the cube of a number or any other mathematical expression is denoted by a superscript of 3. For example, 3^3 = 27.

The cube is also referred to as a number multiplied by its square.

n^3 = n * n^2 = n*n*n

Cube Root

According to mathematics, a cube root is a number multiplied by three times, and we can get the original number.

For example,

Cube of 3 is 27, and cube root of 27 is 3

Let us try with an example:

2**3 = 8

3**3 = 27

4**4 = 256

Example program for finding cube of a number

n= int(input("enter the number:"))
print(cube(n))
def cube(x):
    res = x**3
    return res

Output

The above code is for printing the result type as an integer.

We used a "def" keyword that represents a function. The name of the function is "cube". We are giving input from the user, and the result is x**3; that is, a number is multiplied by itself 3 times.

We can try it for floating point numbers also.

n= float(input("enter the number:"))
print(cube(n))
def cube(x):
    res = x**3
    return res

Output

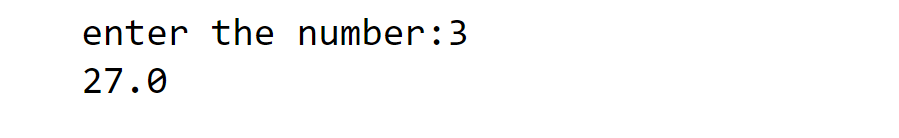
We observed that the result is in the form of a floating point number. It is nothing but a decimal number. We can try with Boolean also.

Cube Root

As discussed above, a cube root is a number multiplied by three times, and we can get the original number.

For example, we write the cube of a number like x**3 and the cube root of a number like x^(1/3).

It is pronounced as x to the power of 1/3.

Example shows us a shred of clear evidence.

27^(1/3) = 3.

Example program for finding cube root

n= float(input("enter the number:"))
print(cube(n))
def cube(x):
    if x<0:
        x = abs(x)
        res = x**(1/3) * (-1)
        return res
    res = x**3
    return res

Output

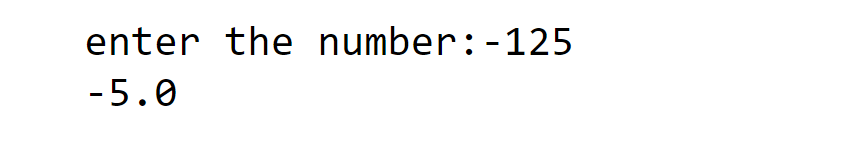
If we want to find a cube, we will multiply a number power 3; if we want a cube root, then we need o find the given number power 1/3. Here, we are not using else for the values equal to or greater than x because here, we used to return. After executing, return control will directly come back to the above return. So, here we will not use the "else" statement.

Another example shows the cube root of a number

a = 64
print(a**(1/3))

Output

4

As we all know that the cube root of 64 is 4. So, it will return 4 and not work for negative integers.

If we want to find the cube root of a negative integer, then we have to make some changes they are:

a = -64
print(-(-a)**(1/3))

Output

-4

We should only give the "-" symbol before the given number and in the print statement.

Using NumPy cbrt() Function

To find a cube root in numpy, we use numpy.cbrt() method. The np.cbrt() function returns the cube root of every element of an array. NumPy cbrt() is a mathematical method to find the cube root of every element in a given array.

Example program

import numpy as np
a1 = [1,8,64,125]
a2 = np.cbrt(a1)
print(a2)

Output

The np.cbrt() function is the easiest method for calculating the cube root of a number. Unlike the above, it does not get in trouble with negative inputs and will return the exact number like 5 for input 125.