Chromatic Number in Java
The chromatic number is the bare minimum of colours necessary to accurately colour any graph. To put it another way, the chromatic number can be thought of as the bare minimum of colours required to colour any graph so that no two neighboring vertices of the graph would be given the same colour.
Graph Colouring
The technique of giving colours to a graph's vertices is known as graph colouring. In this case, the two adjacent vertices shouldn't be filled with the same colour. Vertex colouring is another name for graph colouring. When colouring a graph, we must be careful to ensure that no edge's end vertices have the same colour as the rest of the graph. The term "properly coloured graph" refers to this kind of graph.
With some limitations, the chromatic numbers are typically employed to colour graph nodes. The minimal number of distinct colours needed to colour every node in a graph so that any two neighbouring nodes do not share the same colour is given by chromatic numbers in Java. It has numerous applications. The greedy method will be used in this section to determine a graph's chromatic number.
Steps to find Chromatic Number
Step1: Give the graph's first node the first colour.
Step2: For the last N - 1 node, perform the following.
Consider the presently selected node and give it the colour with the lowest colour number. Providing that none of the nodes nearby that have previously been coloured have had the colour applied. Assign a new colour to the node if all previously used colours are present on the nodes that are nearby.
Examples of Chromatic Number
Java program for Chromatic Number
import java.util.LinkedList;
import java.util.*;
import java.io.*;
//The class displays an adjacency list-based undirected graph.
public class sol
{
private int S; // Number of nodes
private LinkedList<Integer>adjList[]; //Adjacency List
//Constructor
sol(int s)
{
S = s;
adjList = new LinkedList[s];
for (int i = 0; i< n; i++)
{
adjList[i] = new LinkedList();
}
}
// Method to create an edge into the graph from node x to y and y to x
void addingE(int a, int b)
{
// The Graph is not directed
adjList[a].add(b);
adjList[b].add(a);
}
// A method that finds the chromatic number of a graph
void findChromticNo(int arr[])
{
// caculating the size of the array
int size = arr.length;
Set<Integer>hashSet = new HashSet<Integer>();
// iterating over every node and storing its color in the hashset
for(int j = 0; j < size; j++)
{
// hashset only contains unique numbers.
hashSet.add(arr[j]);
}
// finding the chromatic Number of the graph
int chromaticNumber = hashSet.size();
System.out.println("chromatic no of the graph is: " + chromaticNumber);
}
void greedyColorNodes()
{
int res[] = new int[S];
Arrays.fill(res, -1);
res[0] = 0;
booleanavail[] = new boolean[N];
Arrays.fill(avail, true);
// Assign colors to theh remaining S - 1 nodes
for (int s = 1; s<S; s++)
{
Iterator<Integer>itr = adjList[s].iterator() ;
while (itr.hasNext())
{
int i = itr.next();
if (res[i] != -1)
avail[res[i]] = false;
}
// Find the first color that is available
int clr;
for (clr = 0; clr< N; clr++)
{
if (avail[clr])
{
break;
}
}
res[s] = clr; // Assigning the found color
// For the next iteration, resetting the values back to true
Arrays.fill(avail, true);
}
// printing the result
for (int s = 0; s<S; s++)
{
// N->node and C->colour
System.out.println("N " + s + " ---> C - " + res[s]);
}
// for finding the chromatic number of the graph
findChromticNo(res);
}
// main method
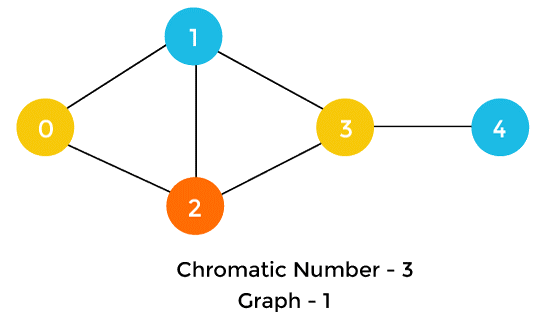
public static void main(String argvs[])
{
// creating a graph that contains
// 5 nodes
Graphs g = new Graphs(5);
// creating edges between nodes
g.addingE(0,1);
g.addingE(0, 1);
g.addingE(1, 2);
g.addingE(1, 3);
g.addingE(2, 1);
g.addingE(3, 4);
System.out.println("Coloring g is: ");
// invoking the method greedyColorNodes() to color the nodes
g.greedyColorNodes();
System.out.println();
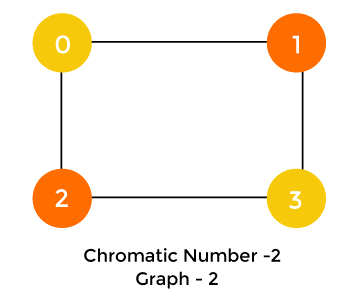
// creating a graph that contains
// 4 nodes
Graphs g2 = new Graphs(4);
System.out.println("Coloring g2 is: ");
// creating edges between nodes
g2.addingE(0, 1);
g2.addingE(0, 2);
g2.addingE(1, 3);
g2.addingE(2, 3);
// invoking the method greedyColorNodes() to color the nodes
g2.greedyColorNodes();
}
}
Output:
Coloring g is:
N 0 ---> C - 0
N 1 ---> C - 1
N 2 ---> C - 2
N 3 ---> C - 0
N 4 ---> C - 1
chromatic number of the graph is: 3
Coloring of the g2 is:
Node 0 ---> Color - 0
Node 1 ---> Color - 1
Node 2 ---> Color - 1
Node 3 ---> Color - 0
The chromatic number of the graph is: 2
Java Program to find Chromatic Index
import java.util.*;
public class CI {
// method to find the chromatic index
public void edgeColoring(int[][] e, int x)
{
// declare a edge to firstedge and color to color 1
int i = 0, color = 1;
// Continue until all the edges have been coloured.
while (i<x) {
// Give the selected edge a color
e[i][2] = color;
boolean flag = false;
// Check by iterating through all other edges.
for (int j = 0; j < e; j++) {
// Ignore if same edge
if (j == i)
continue;
// See if one vertex resembles another.
if ((e[i][0] == e[j][0])
|| (e[i][1] == e[j][0])
|| (e[i][0] == e[j][1])
|| (e[i][1] == e[j][1])) {
// Check if color is similar
if (e[i][2] == e[j][2]) {
// Increase the color by 1
color++;
flag = true;
break;
}
}
}
// If same color faced then repeat again
if (flag == true) {
continue;
}
// / Alternatively, go to a new vertex with colour 1 if not
color = 1;
i++;
}
// Check the maximum color from all the edge colors
int maxColor = -1;
for (i = 0; i<x; i++) {
maxColor = Math.max(maxColor, edges[i][2]);
}
// Print the chromatic index
System.out.println("Chromatic Index = " + maxColor);
}
// Driver code
public static void main(String[] args)
{
// Number of edges
int x = 4;
// Edge list
int[][] e = new int[x][3];
// Initialize all edge colors to 0
for (int i = 0; i< e; i++) {
e[i][2] = -1;
}
// Edges
e[0][0] = 1;
e[0][1] = 2;
e[1][0] = 2;
e[1][1] = 3;
e[2][0] = 3;
e[2][1] = 4;
e[3][0] = 4;
e[3][1] = 1;
// Run the function
chromaticIndexy = new chromaticIndex();
y.edgeColoring(e, x);
}
}
Output:
chromatic Index = 2
Applications of Chromatic Number
- Time table or making schedule:
Imagine having to design a college or university's exam timetable. The individual is knowledgeable about every subject and the pupils enrolled in it. One simple scheduling method is to hold exams for just one subject during a single time frame. As a result, the entire time window will be determined by the total number of available subjects. Such scheduling is ineffective, though, as fewer time periods must be available.
Additionally, it is impossible to arrange all of the exams during a single time period. The reason for this is that a student could enrol in several different subjects. If all of those topics' tests are scheduled for the same time slot, the student can only take the exam for that one subject; the other exams must be missed.
Therefore, it is necessary to reduce the time slots so that there are no conflicts. We use the graph colouring method to do this. The subjects are viewed as nodes, and the only way an edge can exist between two nodes is if a single student is enrolled in both of those subjects. Find the graph's chromatic number after building it. The minimum time periods necessary to correctly administer the exam are indicated by the chromatic number. - Assignment of mobile radio frequency:
The frequencies assigned to each tower must differ when they are all designated at the same site to serve as mobile towers. We require the aid of chromatic numbers to assign the frequencies under this restriction, and the number of frequencies should also be the minimal.
The towers can be thought of as nodes, and an edge connecting these two nodes demonstrates that the towers are close to one another. This is the classic graph colouring problem, where we must lessen the total number of distinct colours, which is determined by the graph's chromatic number.