Counting sort in Java

An array's elements are sorted using the counting sort method, which counts how many times each distinct element appears in the array. The count is kept in an auxiliary array, and the auxiliary array's index is mapped to the count to do the sorting.

Implementing Counting Sort

• Find the largest element (let's call it max) in the provided array.

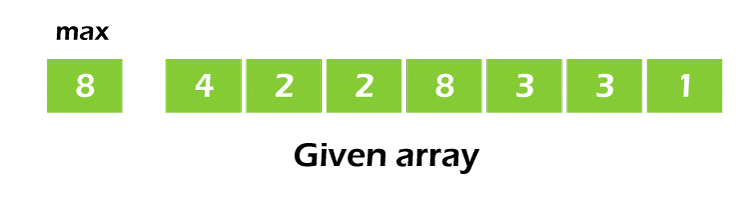
• Make an array with a length of max+1 and all of its items set to 0. The number of elements in the array is kept in this array for counting purposes.

• Adjust the index of each element's count inside the count array.
  For instance, if such count for element 3 is 2, then 2 is placed in the third position of said count array. If element "5" in the array is absent, 0 is kept at the fifth position.

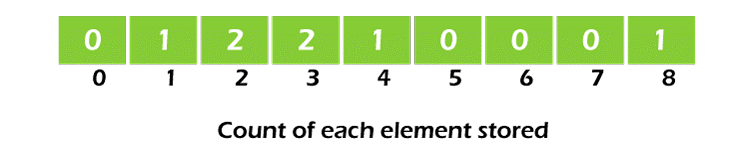
• Count array elements' cumulative sums should be stored. It makes it easier to insert the elements at the proper index in the sorted array.

• In the count array, determine the index of each original array element. This provides the total count. Put the element where the index was determined, as illustrated in the following diagram.

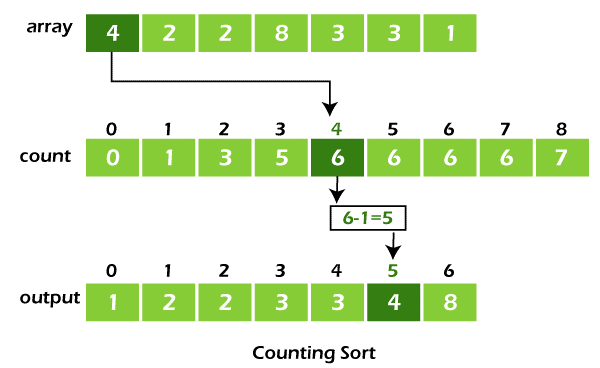
• Once you've positioned each element correctly, deduct one from its count.

Counting sort Algorithm

countingSort(array, size)
max <- find the biggest component of an array
Set the count array to zeroes.
for j <- 0 to size
discover the total number of each distinct element, and then store that number at the jth index in the count array.
for i <- 1 to max
 Find the total and save it directly in the count array.
for j <- size down to 1
 return the array's elements
  reduce the count of each element that has been restored by 1

Java Counting sort Program

CountingSortExpl.java

import java.util.Arrays;
class CountingSortExpl {
void countSort(int a[], int s) {
int[] output = new int[s + 1];
// Determine the array's greatest element
int max = a[0];
for (int i = 1; i < s; i++) {
if (a[i] > max)
   max = a[i];
} int[] count = new int[max + 1];
 // Set up the count array with nothing but zeros
for (int i = 0; i < max; ++i) {
 count[i] = 0;
}
// Save the total number of each element.
for (int i = 0; i < s; i++) {
count[a[i]]++;
}
// Keep track of each array's cumulative count.
for (int i = 1; i <= max; i++) {
count[i] += count[i - 1];
}
// Place the members of the output array in the count array by finding the index 
// of each original array element.
for (int i = s - 1; i >= 0; i--) {
output[count[a[i]] - 1] = a[i];
     count[a[i]]--;
}
// Transform the sorted items into the initial array.
for (int i = 0; i < s; i++) {
a[i] = output[i];
}
}
public static void main(String args[]) {
int[] d = { 8, 2, 3, 4, 1, 3, 2 };
int s = d.length;
  CountingSortExpl c = new CountingSortExpl();
  c.countSort(d, s);
  System.out.println(" Ascending Order Sorted Array: ");
   System.out.println(Arrays.toString(d));
}
}

Output:

Complexity

Time complexity        

Best	O(n+k)
Worst	O(n+k)
Average	O(n+k)

Space Complexity

The space complexity is O(max).

Applications of Counting sort

One uses a counting sort when:

• Smaller numbers can have several counts.
• The requirement is linear complexity.