Radix Sort in Java
Radix Sort in Java
Radix sort in Java uses the digits of the numbers given in the sorted array to sort the numbers. The radix sort uses the place value of digits to do the sorting moving from the LSB (Least Significant Digit) to MSB (Most Significant Digit) of the numbers. By using the counting sort, the quick sort place elements to their appropriate position. Unlike other sorting algorithms, this sorting algorithm never compares numbers to do the sorting. Hence, radix sort is a non-comparative sorting algorithm.
Algorithm and Pseudo Code
// arr -> is the input array to sort
//dig number of digits each integer has
radixSort(arr, dig)
// Uses counting sort for dig number of passes
// Each element in the array has dig number of digits
// consider digits of every number from left to right to do the sorting
for i = 1 to dig do
int freq[] = {0, 0, 0, 0, 0, 0, 0, 0, 0 ,0};
int res[] = new int[arr.length];
// Store the frequency of "digits as keys" in freq[]
// digits as keys - the number that is present at the place i
for j = 0 to sizeOfArr do
increase freq[key of (arr[j]) in the pass i] by 1
end for
for l = 1 to 10 do
freq[l] = freq[l] + freq[l - 1]
end for
// create the resultant array by checking
// the position of arr[i] from freq[k]
for i = size - 1 down to 0 do
res[ freq[key of(arr[i])] ] = arr[j]
reduce freq[key of(arr[i])] by 1
end for
// Now the input array arr[] contains the numbers sorted in
// accordance to current digit place
for j = 0 to size do
arr[j] = res[j]
end for
end for
end radixSort
Java Program
The following code implements radix sort using the pseudo-code defined above.
FileName: RadixSortExample.java
// import statements
import java.util.*;
import java.io.*;
public class RadixSortExample
{
// A utility method to get maximum value element in arr[]
static int findMax(int a[], int size)
{
int max = a[0];
for (int j = 1; j < size; j++)
{
if (a[j] > max)
{
max = a[j];
}
}
return max;
}
// A method to do counting sort of a[] according to
// the digit represented by exp.
static void countSort(int a[], int size, int exponent)
{
int outcome[] = new int[size]; // output array
int countFreq[] = new int[10];
// initializing the array list elements by 0
Arrays.fill(countFreq, 0);
// Keep counting of occurrences in countFreq[]
for (int j = 0; j < size; j += 1)
{
int index = (a[j] / exponent) % 10;
countFreq[index] = countFreq[index] + 1;
}
// Update countFreq[j] so that countFreq[j] now stores
// the appropriate position of the digits in the outcome array
for (int j = 1; j < 10; j++)
{
countFreq[j] = countFreq[j] + countFreq[j - 1];
}
// Compose the outcome array
for (int j = size - 1; j >= 0; j -= 1)
{
int index = (a[j] / exponent) % 10;
outcome[countFreq[index] - 1] = a[j];
countFreq[index] = countFreq[index] - 1;
}
// Copy the output array to a[], so that a[] now
// contains sorted numbers according to curent digit
for (int j = 0; j < size; j++)
{
a[j] = outcome[j];
}
}
// The method that is responsible for doing the sorting for array a of size s
// using radix Sort
static void radixSort(int a[], int s)
{
// to find the maximum number of digits
// we must know the maximum number
int maxEle = findMax(a, s);
// For each and every digit of the number perform counting sort
// Note that numbers or digits of numbers are not passed, exponent is passed.
// It is the exponent that determines which
for (int exponent = 1; maxEle / exponent > 0; exponent *= 10)
{
countSort(a, s, exponent);
}
}
// main method
public static void main(String argvs[])
{
// given input array
int a[] = {326, 453, 608, 835, 751, 435, 704, 690};
// calculating size of the array
int size = a.length;
System.out.println("The array before sorting is: ");
for(int i = 0; i < size; i++)
{
System.out.print(a[i] + " ");
}
System.out.println("\n");
// invoking the method radixSort()
radixSort(a, size);
System.out.println("The array after sorting is: ");
// displaying the sorted array
for(int i = 0; i < size; i++)
{
System.out.print(a[i] + " ");
}
}
}
Output:
The array before sorting is: 326 453 608 835 751 435 704 690 The array after sorting is: 326 435 453 608 690 704 751 835
Explanation: The above program first does the sorting of digits present at the unit place. Then, it performs the sorting again, using counting sort, on the digits present at tens place that is already sorted with the digits present at the unit place. Finally, the program takes the digits present at the hundredth place and does the sorting using counting sort. For simplicity, we have taken all numbers having the same number of digits. The following diagram illustrates the same.
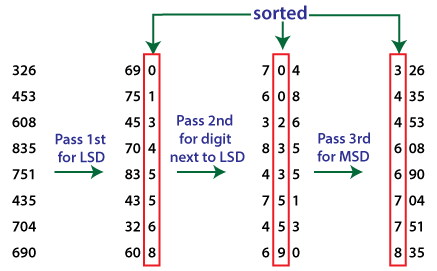
If elements are having a different number of digits, 0 is padded to the element that has a smaller number of digits. For example, if we take 9, 343, 34 then, 9 is considered as 009, 343 as 343, and 9 as 009. Thus, we end up having an equal number of digits for each number.
Analysis of the Radix Sort
Radix sort is a stable sorting algorithm. It uses the concept of bucketing for placing numbers having the same LSB or MSB in the same bucket. Then counting sort decided which number to put first and which one to put later in the bucket. For a large number of inputs, it is found that the radix sort is better than quick sort. However, it is not completely true. If the number of digits increases, then quick sort takes precedence over radix sort.
Time Complexity
Let dig be the number of digits of the largest value element. Let, n be the number of elements in the given input array. Then, the total time complexity of radix sort is O(dig(n + b)), where b is the base used to represent the numbers. In our example, numbers are represented in base 10.
Space Complexity
Space complexity of the radix sort is O(n + k), where n is the total number of elements present in the array, and k is the number of digits present in the maximum element.
Conclusion
Even though the radix sorting algorithm works well than comparison algorithm, for larger numbers the radix sort operation is slow. It should be used where it is required to bucket the elements of almost same category. For lexicographical sorting of strings, the radix sort algorithm can also be used.